Contoh Soal Penerapan pada masalah nyata tentang pertidaksamaan Pecahan
Contoh Soal Penerapan pada masalah nyata tentang pertidaksamaan Pecahan - Sebelum mempelajari topik ini, terlebih dahulu marilah kita mengingat kembali materi pertidaksamaan pecahan. Pertidaksamaan pecahan adalah pertidaksamaan yang mempunyai bentuk pecahan dan mengandung suatu variabel (misal x) pada penyebutnya.
Pertidaksamaan Pecahan Bentuk Linear
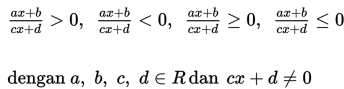
Pertidaksamaan Pecahan Bentuk Kuadrat
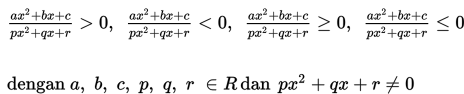
Kedua bentuk pertidaksamaan pecahan di atas dapat diselesaikan dengan cara sebagai berikut :
Agar kalian lebih memahami materi ini, mari kita cermati beberapa contoh soal berikut ini.
Contoh 1:
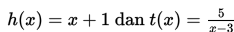
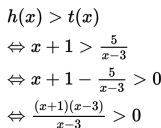

Contoh 2:
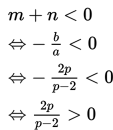
Contoh 3:
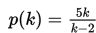
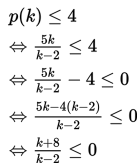
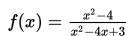
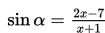
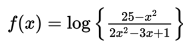
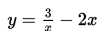
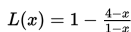
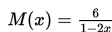
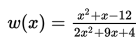
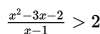
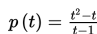
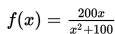
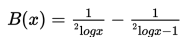
Pertidaksamaan Pecahan Bentuk Linear
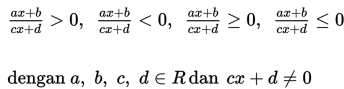
Pertidaksamaan Pecahan Bentuk Kuadrat
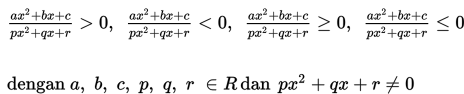
Kedua bentuk pertidaksamaan pecahan di atas dapat diselesaikan dengan cara sebagai berikut :
- Tempatkanlah pembuat nol yang diperoleh dari pembilang dan penyebut pada suatu garis bilangan.
- Periksa tanda dari nilai pecahan ini pada tiap interval yang terbentuk.
- Tentukan himpunan penyelesaian sesuai dengan tanda pertidaksamaannya.
Agar kalian lebih memahami materi ini, mari kita cermati beberapa contoh soal berikut ini.
Contoh 1:
Pak Ahmed sedang mendesain animasi gambar yang melibatkan dua kurva berikut :
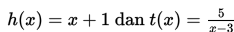
Pak Ahmed menginginkan letak kurva h(x) di atas kurva t(x). Tentukan batas-batas nilai x yang dibutuhkan Pak Ahmed untuk mendesain gambar tersebut!
Penyelesaian :
Agar kurva h(x) di atas kurva t(x) maka nilai h(x) haruslah lebih besar dari t(x).
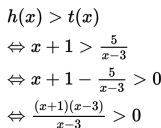
Pembuat nol pembilang :
(x + 1)(x – 3) = 0 <=> x = -1 atau x = 3
(x + 1)(x – 3) = 0 <=> x = -1 atau x = 3
Pembuat nol penyebut :
x – 3 = 0 <=> x = 3
x – 3 = 0 <=> x = 3

Jadi, batas-batas nilai x yang dibutuhkan Pak Ahmed untuk mendesain animasi gambar adalah {x ∈ ℝ| -1 < x < 3}.
Contoh 2:
Sebuah parabola dengan persamaan (p – 2)x2 + 2px + p – 1 = 0 memiliki dua akar, yaitu m dan n. Jika jumlah kedua akar lebih kecil dari nol, berapakah batas-batas nilai p yang memenuhi?
Penyelesaian :
Persamaan parabola (p – 2)x2 + 2px + p – 1 = 0 merupakan persamaan kuadrat dengan
a = p – 2, b = 2, c = p – 1.
a = p – 2, b = 2, c = p – 1.
Oleh karena jumlah akar-akar persamaan kuadrat lebih kecil dari nol, maka
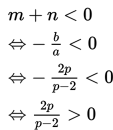
Pembuat nol pembilang :
2p = 0 <=> p= 0
2p = 0 <=> p= 0
Pembuat nol penyebut :
p – 2 = 0 <=> p = 2
p – 2 = 0 <=> p = 2
Jadi, batas-batas nilai p yang memenuhi adalah {p ∈ ℝ | p < 0 atau p > 2}.
Contoh 3:
Seorang ahli gizi wajib mempertimbangkan beberapa faktor saat merancang pola makanan bernutrisi, seperti berat badan dan usia. Oleh karenanya, ahli gizi mempergunakan rumus untuk mengontrol kandungan kalori dalam makanan. Jika unit batas kesehatan tertentu per hari dirumuskan dengan
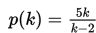
dimana k adalah jumlah kalori makanan. Tentukan batasan kalori per hari agar unit batas kesehatan tidak lebih dari 4 unit!
Penyelesaian :
Oleh karena unit batas kesehatan tidak lebih dari 4 unit, maka
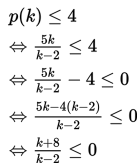
Pembuat nol pembilang :
k + 8 = 0 <=> k = -8
k + 8 = 0 <=> k = -8
Pembuat nol penyebut :
k - 2 = 0 <=> k = 2
k - 2 = 0 <=> k = 2
Jadi, batasan jumlah kalori yang harus dikonsumsi per hari adalah {k ∈ ℝ | -8 ≤ k ≤ 2}.
S1
Sebuah grafik fungsi mempunyai persamaan
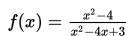
nilai x agar grafik fungsi tersebut selalu terletak di atas sumbu X adalah ....
S2
Rangka yang digunakan untuk membuat springbed adalah suatu kawat per yang letaknya diatur berdasarkan aturan fungsi trigonometri agar kasur itu nyaman dipakai tidur. Jika fungsi yang digunakan adalah
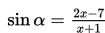
dan sudut yang dibentuk antara dua per yang saling berdekatan tidak lebih dari 90o, maka interval x yang memenuhi adalah ....
S3
Seorang ahli geofisika mempelajari permukaan bumi, termasuk sejarah dari kerak bumi dan bebatuan. Ahli-ahli geofisika juga menyelidiki keberadaan minyak, gas alam, mineral, dan air tanah. Dalam suatu penelitian, diketahui bahwa ada fungsi logaritma yang dapat digunakan untuk melacak intensitas gempa bumi. Fungsi tersebut adalah sebagai berikut :
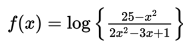
Himpunan nilai x agar fungsi di atas terdefinisi adalah …
S4
Dalam sebuah penelitian, diketahui bahwa gelombang suara dapat dimodelkan dalam sebuah grafik fungsi dengan persamaan sebagai berikut :
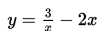
Batas-batas nilai x agar grafik fungsi di atas terletak di atas garis y = x adalah ….
S5
Amir, siswa SMA Quipper sedang belajar tentang penerapan integral dalam kehidupan sehari-hari. Dia mendapat tugas dari gurunya untuk menentukan luas daerah yang dibatasi oleh dua kurva.
Kurva pertama memiliki persamaan
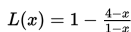
dan kurva kedua memiliki persamaan
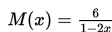
Amir ingin menghitung batas-batas nilai x untuk keperluan dalam perhitungan luas daerah. Batasan nilai x agar kurva L(x) selalu terletak di atas kurva M(x) adalah ....
S6
Berat suatu benda setelah x kali rotasi dalam suatu mesin peringan dapat diukur dengan menggunakan fungsi berikut :
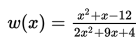
dengan w dalam kilogram. Banyak rotasi minimal yang dibutuhkan agar berat benda lebih besar atau sama dengan nol adalah ….
S7
Sebuah segiempat dibentuk dengan nilai absis memenuhi pertidaksamaan berikut :
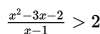
Batas-batas nilai x yang memenuhi pertidaksamaan di atas adalah ....
S8
Penjualan mingguan suatu software dalam t minggu setelah 1 minggu diluncurkan memenuhi fungsi berikut :
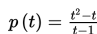
dengan p dalam ribuan. Penjualan software mulai mencapai lebih dari 2000 buah pada minggu ke ….
S9
Populasi kelinci pada suatu pulau setiap tahun dimodelkan sebagai berikut :
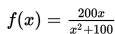
dengan x adalah menyatakan waktu dalam tahun. Populasi kelinci mulai mencapai 800 ekor atau lebih per tahun pada tahun ke- ….
S10
Tingkat kecemerlangan cahaya bintang memenuhi persamaan
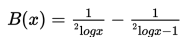
dengan x adalah kecemerlangan yang sesungguhnya dari bintang tersebut dan x > 0. Batas-batas kecemerlangan yang sesungguhnya agar tingkat kecemerlangan cahaya bintang bernilai di bawah 1 adalah ….
