Contoh Soal Penerapan pada masalah nyata tentang pertidaksamaan Irrasional
Contoh Soal Penerapan pada masalah nyata tentang pertidaksamaan Irrasional - Dalam topik ini kalian akan belajar mengenai penerapan pertidaksamaan irasional pada masalah nyata.
Pertidaksamaan irrasional adalah pertidaksamaan yang variabelnya terletak di bawah tanda akar.

Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
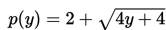
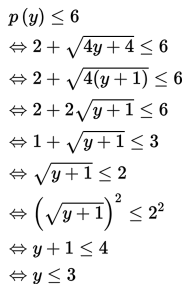
Contoh 2 :
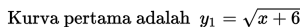
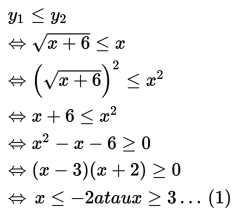
Contoh 3 :
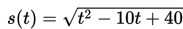
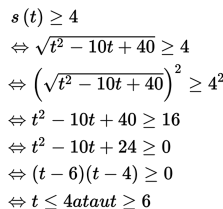
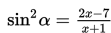
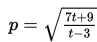
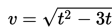
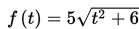
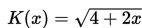
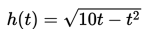
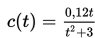
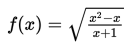
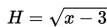
Pertidaksamaan irrasional adalah pertidaksamaan yang variabelnya terletak di bawah tanda akar.
Ada dua bentuk umum pertidaksamaan bentuk akar, yaitu :

Dalam menyelesaikan pertidaksamaan irasional terdapat syarat tambahan selain ketentuan umum, yaitu :
- Bentuk bilangan yang berada di bawah tanda akar adalah ≥ 0.
Misalnya: pada √(x – 2), harus berlaku x – 2 ≥ 0.
- Bilangan bilangan hasil penarikan akar adalah ≥ 0.
Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
Perusahaan asuransi melakukan perhitungan premi yang akan dibayarkan kepada pemegang polis dalam kurun waktu tertentu. Besar premi yang akan dibayarkan memenuhi persamaan berikut :
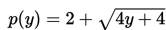
Tentukan batas kurun waktu y (dalam bulan) yang diperlukan oleh pemegang polis agar mendapat premi paling banyak 6 unit!
Penyelesaian :
Agar pemegang polis mendapat premi paling banyak 6 unit, maka p(y) haruslah kurang dari atau sama dengan enam.
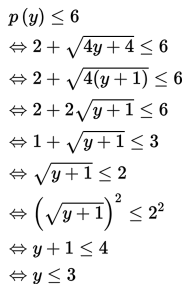
Syarat tambahan : y + 1 ≥ 0 <=> y ≥ -1
Dengan demikian. himpunan penyelesaian dari pertidaksamaan di atas adalah { -1 ≤ y ≤ 3 }.
Jadi, batas kurun waktu yang diperlukan oleh pemegang polis agar mendapat premi paling banyak 6 unit adalah 0 sampai 3 bulan.
Contoh 2 :
Pak Hasrul, guru bimbingan konseling sedang membuat laporan berupa grafik tingkat ketidakhadiran siswa selama satu bulan proses belajar berlangsung. Pak Hasrul dihadapkan dengan dua kurva yang akan digambarkan pada kertas milimeter.
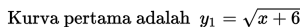
dan kurva kedua adalah y2 = x. Tentukan batas-batas nilai x yang dibutuhkan Pak Hasrul dalam menyelesaikan perhitungan jika disyaratkan kurva y1 harus selalu berada di bawah kurva y2!
Penyelesaian :
Agar kurva y1 selalu berada di bawah kurva y2, maka y1 haruslah lebih kecil dari y2.
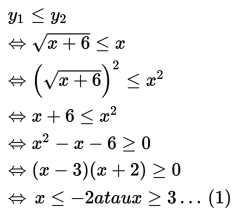
Syarat tambahan : x + 6 ≥ 0 <=> x ≥ -6 ……. (2)
Irisan dari (1) dan (2) merupakan himpunan penyelesaian pertidaksamaan di atas. Dengan demikian, himpunan penyelesaiannya adalah { -6 ≤ x ≤ -2 atau x ≥ 3 }.
Contoh 3 :
Sebuah sepeda melaju di jalan raya selama t detik dengan panjang lintasan (dalam meter) ditentukan oleh persamaan berikut :
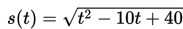
Jika panjang lintasan sepeda sekurang-kurangnya adalah 4 meter, tentukan nilai t yang memenuhi!
Penyelesaian :
Oleh karena panjang lintasan sepeda sekurang-kurangnya adalah 4 meter, maka s(t) haruslah lebih besar atau sama dengan empat.
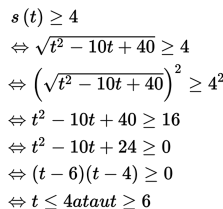
Syarat tambahan :
t2 – 10t + 40 ≥ 0 → selalu terpenuhi, karena t2 – 10t + 40 definit positif (a > 0 dan D < 0).
Dengan demikian, nilai t yang memenuhi adalah t ≤ 4 detik atau t ≥ 6 detik.
S1
Sebuah gelombang radio menggunakan frekuensi gelombang bunyi yang dapat dimodelkan sebagai fungsi trigonometri
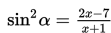
Batas-batas nilai x yang memenuhi agar gelombang bunyi tersebut dapat terdeteksi adalah ...
S2
Dua buah vektor gaya R1 dan R2 disusun saling tegak lurus. Resultan kedua vektor diwakili oleh vektor Rt. Jika vektor R2 = 5 newton dan vektor R1 tidak kurang dari 15 newton. Jangkauan nilai vektor R1 adalah ...
S3
Pada peluncuran produk suatu handphone, penjualan per periode mengalami peningkatan secara drastis, untuk kemudian berkurang secara berkala. Diasumsikan bahwa penjualan per periode sebanyak p ribu unit dalam t periode setelah peluncuran pertama dirumuskan dengan
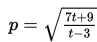
Penjualan akan mencapai 3 unit atau lebih pada interval waktu ....
S4
Kecepatan sebuah benda setelah t detik dirumuskan
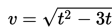
dalam satuan meter/detik. Batasan nilai t agar benda tersebut memiliki kecepatan maksimum sebesar 2 meter/detik adalah ..
S5
Sebuah daerah telah berhasil berswasembada beras sejak tahun 2013. Setiap tahun beras yang dihasilkan daerah tersebut makin meningkat. Jumlah beras yang dihasilkan setelah t tahun dirumuskan dengan
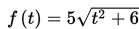
dalam satuan ton. Jumlah waktu minimal agar beras yang dihasilkan daerah tersebut minimal dapat mencapai 25 ton adalah ....
S6
Keuntungan dalam sehari suatu pabrik pembuatan produk elektronik yang memproduksi x unit barang elektronik tertentu diberikan oleh
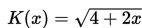
juta rupiah. Agar keuntungan yang diperoleh minimal 7 juta rupiah, berapa unit barang elektronik yang harus diproduksi oleh pabrik tersebut?
S7
Sebuah peluru yang ditembakkan ke atas mencapai ketinggian
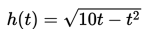
meter dalam t detik. Selama berapa detik peluru tersebut berada pada ketinggian tidak kurang dari 10√2 meter?
S8
Suatu obat yang berbentuk cairan injeksi disuntikkan ke dalam tubuh pasien. Cairan injeksi itu masuk dan mengalir ke dalam aliran darah pasien melalui lengan kanan. Konsentrasi obat (dalam mg/ml) dalam aliran darah lengan kiri pasien t jam setelah diinjeksikan didekati dengan persamaan
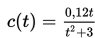
Konsentrasi obat dalam lengan kiri pasien lebih besar atau sama dengan 0,03 mg/ml terjadi saat ....
S9
Seorang mahasiswa jurusan arsitek sedang merancang sebuah model rute perjalanan yang menghubungkan beberapa kota (vertex), rute perjalananan tersebut dimodelkan sebagai fungsi
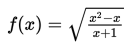
dengan x adalah banyaknya kota (vertex). Agar fungsi yang dibuat tersebut dapat terdefinisi, nilai x positif yang memenuhi adalah ...
S10
Hasil produksi suatu barang yang cacat dinyatakan dengan persamaan
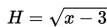
unit untuk x bahan campuran. Agar hasil produksi yang cacat (H) kurang dari 7 unit, maka banyaknya campuran yang diperlukan adalah ...
