Contoh Soal Penerapan pada masalah nyata tentang pertidaksamaan mutlak
Contoh Soal Penerapan pada masalah nyata tentang pertidaksamaan mutlak - Dalam topik kali ini, kalian akan belajar mengenai beberapa contoh pertidaksamaan nilai mutlak pada masalah nyata.
Pertidaksamaan nilai mutlak adalah pertidaksamaan yang variabelnya berada di dalam tanda mutlak. Adapaun bentuk umum pertidaksamaan nilai mutlak linear adalah sebagai berikut :
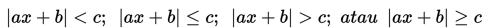
Selanjutnya, untuk untuk menyelesaikan pertidaksamaan nilai mutlak digunakan sifat-sifat nilai mutlak sebagai berikut :
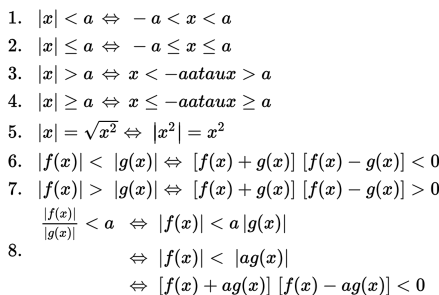
Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :

Contoh 2 :
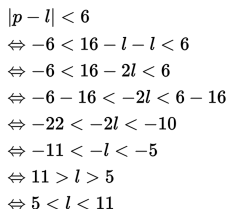
Contoh 3 :
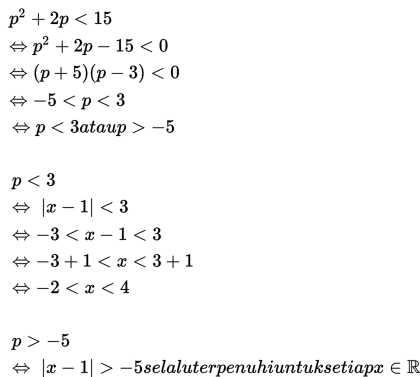
Pertidaksamaan nilai mutlak adalah pertidaksamaan yang variabelnya berada di dalam tanda mutlak. Adapaun bentuk umum pertidaksamaan nilai mutlak linear adalah sebagai berikut :
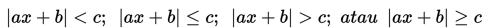
dengan a, b, c adalah konstanta dan a ≠ 0.
Selanjutnya, untuk untuk menyelesaikan pertidaksamaan nilai mutlak digunakan sifat-sifat nilai mutlak sebagai berikut :
Untuk x , a ∈ R dan a ≥ 0 berlaku :
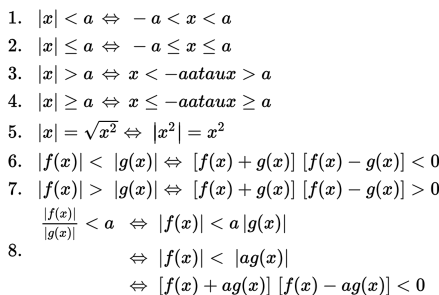
Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
Jarak terpendek yang diperlukan untuk menghentikan suatu mobil sejak pengereman dilakukan disebut jarak henti. Jarak henti ini merupakan faktor penting yang perlu diuji sebelum peluncuran produk mobil baru. Data mengenai jarak henti dapat digunakan untuk menghitung waktu reaksi pengemudi (selang waktu mulai pengemudi melihat kejadian sampai dia bereaksi menginjak pada rem) berdasarkan tingkat kelajuan mobil (dalam meter/jam).
Suatu penelitian menyatakan bahwa jarak henti dapat dinyatakan dengan formula :
d = |0,44v2 + 1,1v|, dimana v adalah kelajuan dan d dalam meter.
d = |0,44v2 + 1,1v|, dimana v adalah kelajuan dan d dalam meter.
Pada batas kelajuan berapakah jarak henti mobil lebih dari 100 meter?
Penyelesaian :
Oleh karena kelajuan selalu bernilai positif, maka |0,44v2 + 1,1v| = 0,44v2 + 1,1v. Selanjutnya, agar jarak henti mobil lebih dari 100 meter, maka d haruslah lebih besar dari seratus.

Jadi, batas kelajuannya jarak henti mobil lebih dari 100 meter adalah
-16,4 < v < 13,9 meter/jam.
-16,4 < v < 13,9 meter/jam.
Contoh 2 :
Selisih antara panjang dan lebar suatu persegi panjang kurang dari 6 cm. Jika keliling persegi panjang adalah 32 cm, maka tentukan batas nilai lebar persegi panjang tersebut!
Penyelesaian :
Oleh karena keliling persegi panjang adalah 32 cm, maka
2(p + l) = 32
<=> p + l = 16
<=> p = 16 - l
2(p + l) = 32
<=> p + l = 16
<=> p = 16 - l
Selanjutnya, karena selisih antara panjang dan lebar persegi kurang dari 6 cm, maka
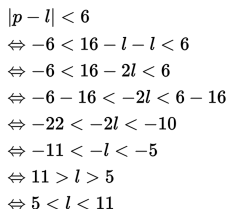
Dengan demikian, batas nilai lebar persegi panjang yang dimaksud adalah antara 5 cm sampai dengan 11 cm.
Contoh 3 :
Pergerakan suatu titik dalam koordinat kartesius ditentukan oleh nilai absis dan memenuhi pertidaksamaan |x – 1|2 + 2|x – 1| < 15. Tentukan nilai x yang memenuhi pertidaksamaan tersebut!
Penyelesaian :
Jika dimiisalkan |x – 1| = p, maka diperoleh hasil sebagai berikut :
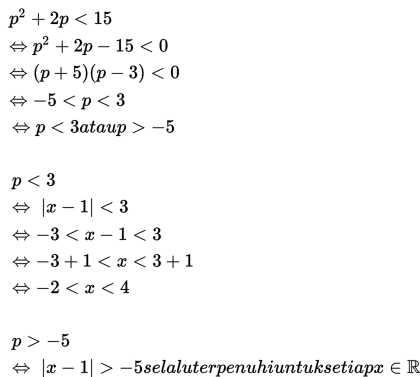
jadi, nilai x yang memenuhi adalah { x ∈ ℝ | -2 < x < 4 }.
S1
Luas suatu daerah yang memenuhi pertidaksamaan
|3 – 2x| < 4. Batas-batas nilai x yang memenuhi luas daerah tersebut adalah ....
|3 – 2x| < 4. Batas-batas nilai x yang memenuhi luas daerah tersebut adalah ....
S2
Ordinat suatu benda ditentukan oleh nilai absis. Jika posisi benda digambarkan dalam koordinat kartesius, maka berlaku persamaan y = |x2 - 6|. Batas nilai x agar ordinat maksimum 3 meter adalah ....
S3
Dodi membuat lintasan bola berbentuk parabola dengan waktu t detik, sebagai fungsi tinggi h meter. Persamaan lintasannya adalah h = |10t – 2t2|. Selama selang berapa detik bola berada pada ketinggian di atas 8 meter?
S4
Sebuah komet mempunyai lintasan yang memenuhi pertidaksamaan |x – 2|2 > 4|x – 2| + 12. Nilai x yang memenuhi pertidaksamaan tersebut adalah ....
S5
t adalah jumlah bagian tanah waris yang akan diterima oleh Sunu. Diketahui bahwa t merupakan suatu pecahan dengan pembilang x2 - 3 dan penyebut 3x + 7. Agar
log (1 - |t|) terdefinisi, maka nilai x yang memenuhi adalah ....
log (1 - |t|) terdefinisi, maka nilai x yang memenuhi adalah ....
S6
Pada mobil-mobil baru, angka kilometer per liternya tergantung pada bagaimana mobil itu digunakan, apakah sering digunakan untuk perjalanan jarak jauh ataukah hanya untuk perjalanan jarak dekat (dalam kota). Untuk suatu merek mobil tertentu, angka kilometer per liternya berkisar di angka 2,8 kurang atau lebihnya dari 12 km/L. Jangkauan dari angka km/L dari mobil tersebut adalah ...
S7
Ketika memancing di laut dalam, kedalaman optimal dalam menangkap jenis ikan tertentu memenuhi pertidaksamaan 8|d – 150| - 432 < 0 (dalam meter). Jangkauan kedalaman yang dianjurkan untuk menangkap jenis ikan tersebut adalah ....
S8
Pada suatu hari, rata-rata kepadatan lalu lintas di suatu perempatan adalah 726 mobil per jam (mpj). Selama jam sibuk, kepadatan lalu lintasnya lebih tinggi, sedangkan selama jam longgar kepadatannya lebih rendah. Jangkauan dari kepadatan lalu lintas di perempatan tersebut jika kepadatannya tidak pernah lebih atau kurang 235 mpj dari rata-rata adalah ….
S9
Setiap anggota batalion wajib lari mengelilingi tenda dengan rata-rata banyak putaran adalah 125 kali tiap harinya. Jika setiap anggota, selisih banyaknya putaran setiap anggota tidak akan lebih 23 dari rata-rata, maka jangkauan banyaknya putaran yang harus dilakukan oleh setiap anggota batalion adalah ....
S10
Berdasarkan aturan resmi dari olahraga golf, bisbol, biliar, dan boling, (a) ukuran bola golf harus tidak lebih dan kurang 0,03 mm dari d = 42,7 mm, (b) ukuran bola bisbol harus tidak lebih dan kurang 1,01 mm dari d = 73,78 mm, (c) ukuran bola biliar harus tidak lebih dan kurang 0,127 mm dari d = 57,15 mm, dan (d) ukuran bola boling harus tidak lebih dan kurang 12,05 mm dari d = 217,105 mm. Olahraga yang memberikan toleransi t (t = interval lebar/diameter rata-rata) yang paling kecil adalah ...
