Contoh Soal Konsep dan aturan pada bidang datar
Contoh Soal Konsep dan aturan pada bidang datar - Titik adalah suatu satuan dasar dari geometri, sedangkan garis adalah sederetan titik-titik yang jumlahnya sangat banyak (tak terhingga), yang memanjang pada dua arah yang berlawanan tanpa ujung. Dalam gambar di bawah ini, A dan B adalah titik dan a adalah garis yang menghubungkan titik A dan B. Untuk kedepannya, garis digambar tanpa menggunakan anak panah.
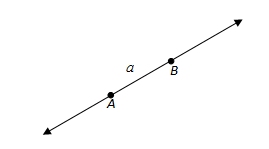
Jika sebuah garis dipotong menjadi beberapa bagian, maka penggalan garis tersebut dinamakan segmen garis. Adapun panjang segmen garis adalah jarak antara kedua titik ujungnya. Dalam gambar di atas, jika garis a dipotong pada titik A dan B, maka kita akan memperoleh segmen garis AB.

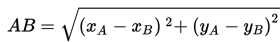
Jika dua buah garis kita hubungkan, maka kedua garis tersebut akan membentuk sudut. Besar sudut antara dua garis ini dapat bervariasi.
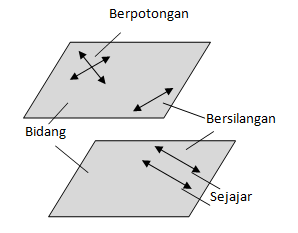
Bidang adalah permukaan datar yang diperpanjang tak terhingga ke segala arah. Setiap garis yang saling berpotongan akan terletak pada satu bidang, sedangkan garis-garis yang saling bersilangan tidak terletak pada satu bidang.
Mari perhatikan gambar di bawah ini.
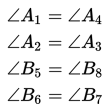
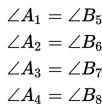
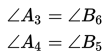
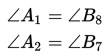
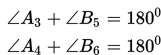
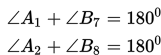

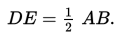
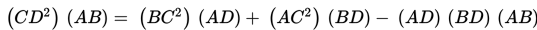
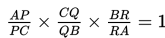

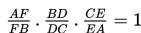
Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
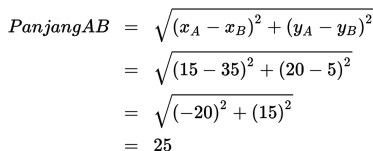
Contoh 2 :
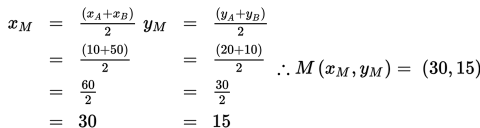
Contoh 3 :
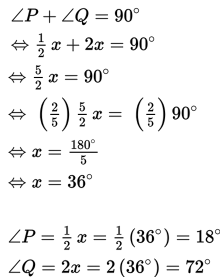
Contoh 4 :
Contoh 5 :
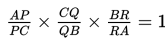
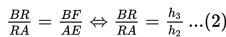
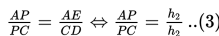
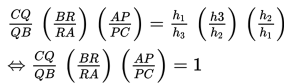

Postulat 1 : Paling sedikit diperlukan dua titik untuk membuat sebuah garis.
Postulat 2 :Dua titik yang berbeda hanya dihubungkan oleh satu garis.
Jika sebuah garis dipotong menjadi beberapa bagian, maka penggalan garis tersebut dinamakan segmen garis. Adapun panjang segmen garis adalah jarak antara kedua titik ujungnya. Dalam gambar di atas, jika garis a dipotong pada titik A dan B, maka kita akan memperoleh segmen garis AB.
Postulat : Panjang setiap segmen garis adalah suatu bilangan positif yang khas (tunggal).

Dalam gambar di atas, panjang segmen garis AB adalah
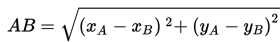
Jika dua buah garis kita hubungkan, maka kedua garis tersebut akan membentuk sudut. Besar sudut antara dua garis ini dapat bervariasi.
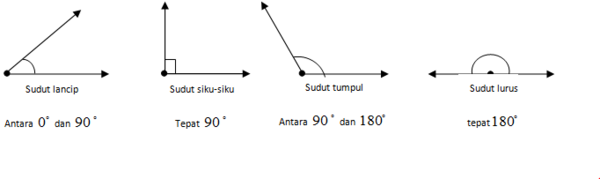
- Jika sudut yang terbentuk berkisar antara 0o hingga 90o, maka sudut antara kedua garis tersebut disebut sudut lancip.
- Jika sudut yang terbentuk adalah 90o, maka kedua garis dikatakan saling berpenyiku dan sudut antara kedua garis tersebut disebut sudut siku-siku.
- Jika sudut yang terbentuk berkisar antara 90o hingga 180o, maka sudut antara kedua garis tersebut disebut sudut tumpul.
- Jika sudut yang terbentuk adalah 180o, maka kedua garis dikatakan saling berpelurus dan sudut antara kedua garis tersebut disebut sudut lurus.

Nah, sekarang kalian sudut tahu apa itu titik dan garis, serta macam-macam sudut. Lalu, apa yang dimaksud dengan bidang?
Bidang adalah permukaan datar yang diperpanjang tak terhingga ke segala arah. Setiap garis yang saling berpotongan akan terletak pada satu bidang, sedangkan garis-garis yang saling bersilangan tidak terletak pada satu bidang.

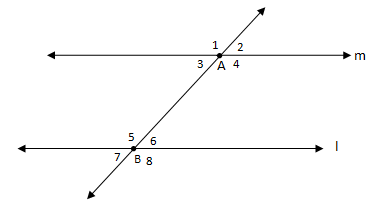
Mari perhatikan gambar di bawah ini.

a. Jika dua garis berpotongan, maka pasangan sudut yang saling bertolak belakang adalah sama besarnya.
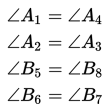
b. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut-sudut yang sehadap adalah sama besarnya.
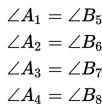
c. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut dalam berseberangan adalah sama besarnya.
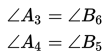
d. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut luar berseberangan adalah sama besarnya.
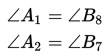
e. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut dalam sepihak jumlahnya 180o.
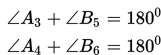
f. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut luar sepihak jumlahnya 180o.
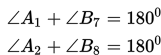
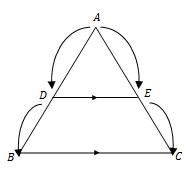
Dalil titik tengah segitiga
Segmen garis penghubung titik-titik tengah dari kedua sisi segitiga adalah sejajar dengan sisi ketiga dan panjangnya adalah setengah kali panjang sisi ketiga tersebut.

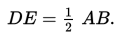
Dalil Intercept Segitiga
Jika sebuah garis sejajar dengan salah satu sisi sebuah segitiga ABC (misalnya garis sejajar sisi BC) memotong dua sisi lain dari segitiga ABC (yaitu sisi AB danAC) di titik D dan E, maka berlaku perbandingan berikut ini :
- AD : DB = AE : EC
- AD : AB = AE : AC = DE : BC

Dalil Stewart
Dalam segitiga sembarang selalu berlaku: kuadrat panjang garis yang ditarik dari titik sudut ke rusuk di hadapannya dikali panjang rusuk di hadapannya tersebut, sama dengan jumlah kuadrat panjang kedua rusuk lainnya setelah masing-masing dikali bersilang dengan panjang bagian-bagian rusuk ketiga dikurangi hasil perkalian berganda di antara panjang rusuk ketiga tersebut dengan bagian-bagiannya.
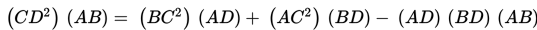
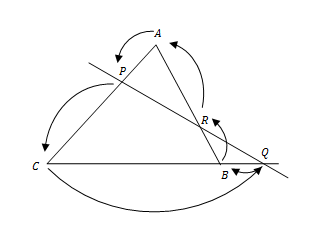
Dalil Menelaus
Jika sebuah garis berpotongan dengan ketiga sisi ΔABC (sisi-sisi AB, BC, CA) atau perpanjangan masing-masing di P, Q, dan R, maka berlaku
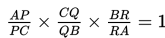

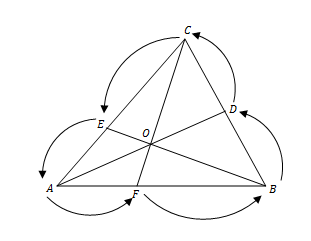
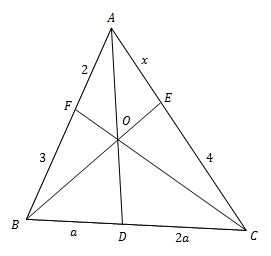
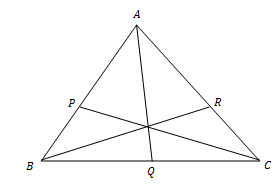
Dalil de Ceva
Jika garis yang ditarik dari tiap titik sudut segtiga (titik A, B, dan C) berpotongan pada satu titik (titik O) dan memotong sisi-sisi yang berhadapan (sisi BC, CA, dan AB) di titik D, E, dan F, maka berlaku :
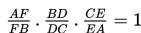

Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
Diberikan titik A(15, 20) dan titik B(35, 5). Tentukan panjang segmen garis AB !
Penyelesaian :
- A (15, 20), berarti xA = 15 dan yA = 20
- B (35,5), berarti xB = 35 dan yB = 5
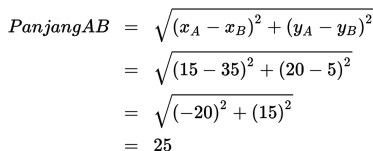
Contoh 2 :
Tentukan koordinat titik tengah M dari segmen garis AB, dengan A(10, 20) dan B(50, 10) !
Penyelesaian :
- A(10, 20), berarti xA = 10 dan yA = 20
- B(50, 10), berarti xB = 50 dan yB = 10
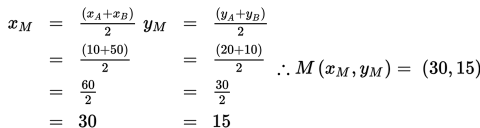
Contoh 3 :
∠P dan ∠Q saling berpenyiku, ∠P = ½ x dan ∠Q = 2x. Tentukan besar ∠P dan ∠Q !
Penyelesaian :
Oleh karena ∠P dan ∠Q saling berpenyiku, maka jumlah kedua sudut tersebut sama dengan 90o.
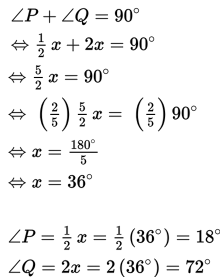
Contoh 4 :
Hengki memiliki dua segmen garis sepanjang 7 cm dan 4 cm. Jika Hengki hendak membuat segitiga dari dua segmen garis tersebut, maka tentukan panjang segmen garis ketiga!
Penyelesaian :
- Jumlah panjang kedua garis = 7 cm + 4 cm = 11 cm
- Selisih panjang kedua garis = 7 cm 4 cm = 3 cm
Jika dimisalkan panjang segmen garis ketiga adalah x cm, maka agar terbentuk segitiga, haruslah berlaku : 3 cm < x <11 cm.
Dengan demikian, panjang segmen garis ketiga lebih besar dari 3 cm namun kurang dari 11 cm.
Contoh 5 :

Berdasarkan dalil Menelaus, pada gambar di atas berlaku hubungan
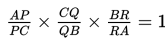
Buktikanlah dalil tersebut!
Penyelesaian :
Buat garis bantu CD ⊥ PQ dan BF ⊥ PQ seperti ditunjukkan pada gambar.

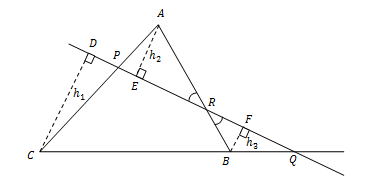
Berdasarkan gambar di atas, ∠Q = ∠Q, ∠D = ∠F = 90o, dan ∠DCQ = ∠FBQ. Dengan demikian, ΔCDQ sebangun dengan ΔBFQ dan berlaku perbandingan berikut :
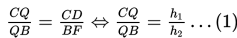
Oleh karena ΔBRF juga sebangun dengan ΔARE (sd-sd-sd), maka berlaku perbandingan berikut :
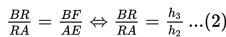
Selanjutnya, karena ΔAPE juga sebangun dengan ΔCPD (sd-sd-sd), maka berlaku perbandingan :
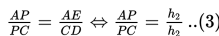
Apabila ruas kiri dari persamaan (1), (2), dan (3) dikalikan, maka diperoleh hasil sebagai berikut :
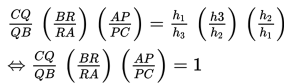
S1
Diberikan segitiga ABC. Titik D dan E berturut-turut pada sisi AC dan BC. Jika AB = 12 satuan, CD = DA, CE = EB, AC // BF, FB = 5 satuan, dan CEB adalah garis lurus, maka panjang DE dan AC berturut-turut adalah ....
S2
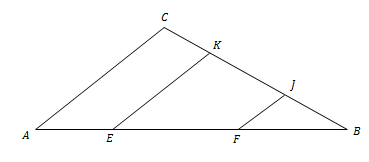
Perhatikan ΔABC pada gambar berikut.

Diketahui bahwa AE = BF dan AC // EK // FJ.
Pernyataan berikut yang benar adalah ....
Pernyataan berikut yang benar adalah ....
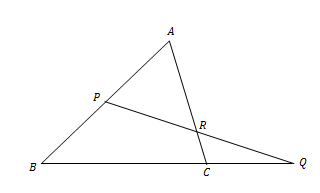
S3
Diberikan segitiga seperti tampak pada gambar berikutini.

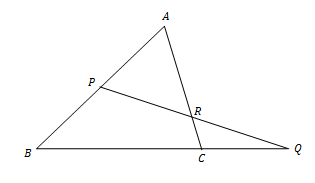
Jika AP : PB = 3 : 2, BC : CQ = 5 : 3, maka AR : RC = …..
S4
Diberikan gambar berikut.

Jika AP : PB = 3 : 2, BC : CQ = 5 : 3 maka QR : RP = ….
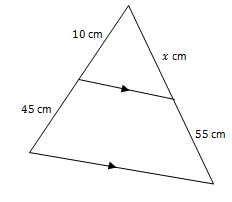
S5
Diberikan segitiga seperti tampak pada gambar berikut.

Nilai x adalah ....
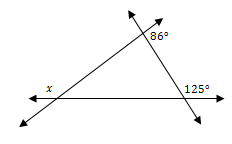
S6
Perhatikan segitiga pada gambar berikut.

Nilai x mendekati ....
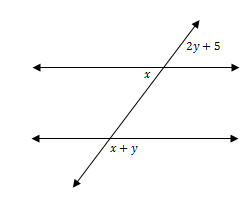
S7
Diberikan gambar berikut.

Nilai x + y adalah ….
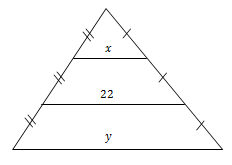
S8
Dalam segitiga ABC berikut ini diketahui bahwa AB = 5, AP = 4, AC = 8 dan AR = 5.

Rasio BQ : BC adalah ....
S9
Perhatikan gambar berikut ini.

Nilai x yang memenuhi adalah ….
S10
Diberikan gambar berikut :

Nilai x adalah ....
