Contoh Soal Pemecahan masalah nyata dengan menerapkan sifat-sifat geometri bidang datar
Contoh Soal Pemecahan masalah nyata dengan menerapkan sifat-sifat geometri bidang datar - Pada topik sebelumnya, kalian telah mempelajari konsep dan aturan pada bidang datar, sedangkan dalam topik ini kalian akan belajar mengenai penerapannya dalam masalah nyata.
Mari kita ingat kembali beberapa konsep dan aturan pada bidang datar.
Sudut dan Garis

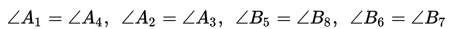
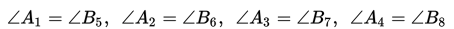
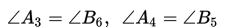
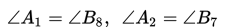
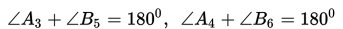
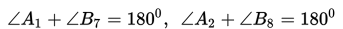
Dalil Titik Tengah Segitiga
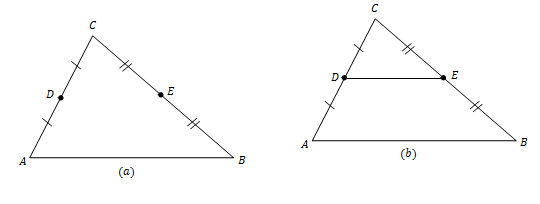
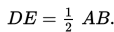
Dalil Intercept Segitiga
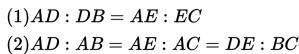
Dalil Stewart

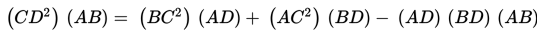
Dalil Menelaus
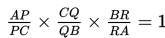
Dalil de Ceva

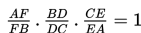
Apakah kalian sudah paham? Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :

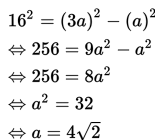
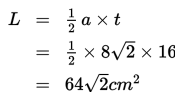
Contoh 2 :
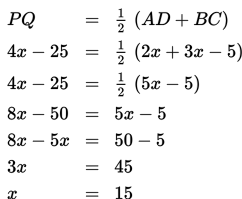
Contoh 3 :
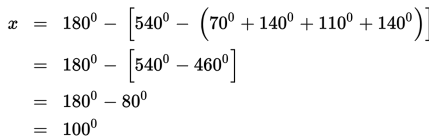
Mari kita ingat kembali beberapa konsep dan aturan pada bidang datar.
Sudut dan Garis

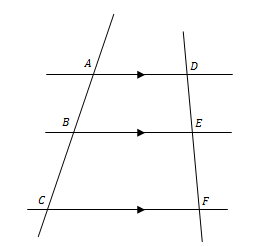
a. Jika dua garis berpotongan, maka pasangan sudut yang saling bertolak belakang adalah sama besarnya.
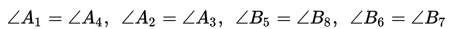
b. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut-sudut yang sehadap adalah sama besarnya.
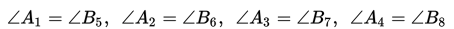
c. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut dalam berseberangan adalah sama besarnya.
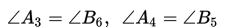
d. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut luar berseberangan adalah sama besarnya.
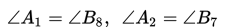
e. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut dalam sepihak jumlahnya 180o.
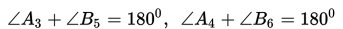
f. Jika dua garis sejajar dipotong oleh sebuah garis transversal, maka pasangan sudut luar sepihak jumlahnya 180o.
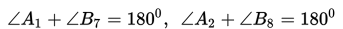
Dalil Titik Tengah Segitiga
"Segmen garis penghubung titik-titik tengah dari kedua sisi segitiga adalah sejajar dengan sisi ketiga dan panjangnya adalah setengah kali panjang sisi ketiga tersebut."
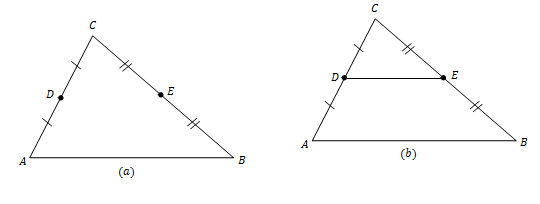
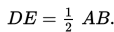
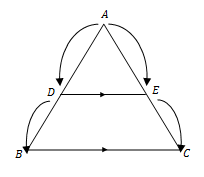
Dalil Intercept Segitiga
"Jika sebuah garis sejajar dengan salah satu sisi sebuah segitiga ABC (misal garis tersebut sejajar sisi BC) dan memotong dua sisi lain dari segitiga tersebut (yaitu sisi AB dan AC) di titik D dan E, maka berlaku persamaaan kesebandingan sebagai berikut :"

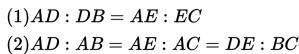
Dalil Stewart
Dalam segitiga sembarang selalu berlaku :
- Kuadrat panjang garis yang ditarik dari suatu titik sudut ke rusuk di hadapannya dikali panjang rusuk di hadapannya sama dengan jumlah kuadrat panjang kedua rusuk lainnya setelah masing-masing dikali bersilang dengan panjang bagian-bagian rusuk ketiga dikurangi hasil perkalian berganda di antara panjang ketiga rusuk tersebut dengan bagian-bagiannya.

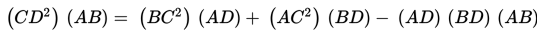
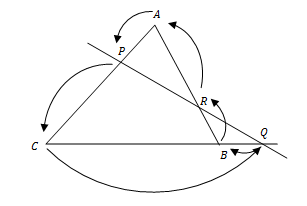
Dalil Menelaus
Jika sebuah garis berpotongan dengan ketiga sisi ΔABC atau perpanjangan, maka berlaku :

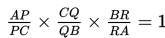
Dalil de Ceva
Jika garis yang ditarik dari tiap titik sudut segtiga (titik A, B, dan C) berpotongan pada satu titik (titik O) dan memotong sisi-sisi yang berhadapan (sisi BC, CA, dan AB) di titik D, E, dan F, maka berlaku :

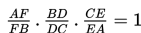
Apakah kalian sudah paham? Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
Sebuah palang berbentuk segitiga sama kaki. Alas dan sebuah kakinya memiliki perbandingan 2 : 3 dengan tinggi segitiga 16 cm. Hitung luas segitiga tersebut!
Penyelesaian :
Pada segitiga siku-siku, berlaku Teorema Pythagoras, sehingga diperoleh hasil sebagai berikut :

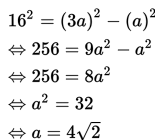
Dengan demikian, panjang alas segitiga adalah
2a = 2(4√2) = 8√2 cm
2a = 2(4√2) = 8√2 cm
Jadi, luas segitiga tersebut adalah
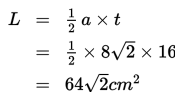
Contoh 2 :

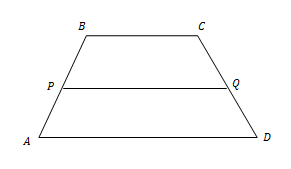
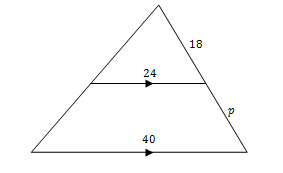
Pada trapesium ABCD di atas, BC // AD, P titik tengah AB dan Q titik tengah CD.
Jika BC = 2x, PQ = 4x – 25, dan AD = 3x – 5, maka tentukan panjang AD, BC, dan PQ!
Jika BC = 2x, PQ = 4x – 25, dan AD = 3x – 5, maka tentukan panjang AD, BC, dan PQ!
Penyelesaian :
Berdasarkan sifat kesebangunan, panjang garis tengah trapesium sama dengan setengah kali jumlah panjang sisi-sisi sejajarnya.
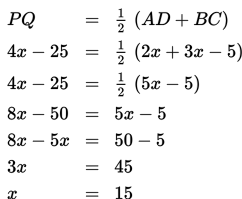
Dengan demikian,
- AD = 3x -5 = 3(15) - 5 = 40
- BC = 2x = 2(15) = 30
- PQ = 4x - 25 = 4(15) - 25 = 35
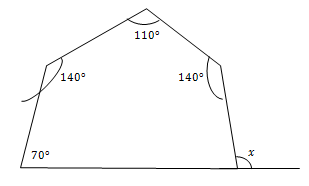
Contoh 3 :
Sebuah lapangan berbentuk segi-5 seperti tampak pada gambar.

Tentukan besar sudut x !
Penyelesaian :
Oleh karena sudut pusat dalam setiap segitiga di dalam segi-5 beraturan adalah 720, maka jumlah semua sudut dalam segi-5 adalah 540o.
Dengan demikian,
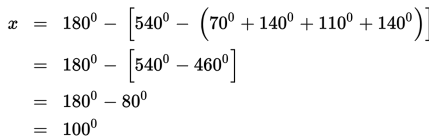
S1
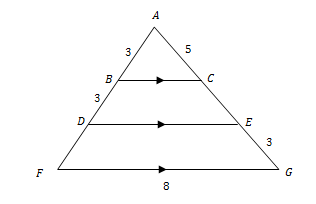
Gambar berikut menunjukkan bagian dari sebuah jembatan yang dibuat dari kabel-kabel menggantung dari suatu balok besi penopang ke permukaan mendatar jembatan.

Jika AB = (x + 2) m, BC = 12 m, DE = 6 m, dan EF = 8 m, maka panjang AC adalah ....
S2
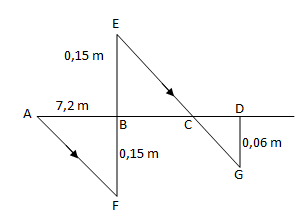
Suatu alat peraga fisika digunakan untuk memindahkan beban pada balok penyangga tegangan dengan ilustrasi sebagai berikut :

Jika jarak A ke B adalah 7,2 m, maka panjang AD adalah ....
S3
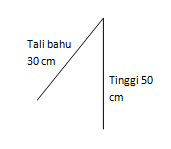
Rudi sedang mendesain sebuah ransel dan perlu menentukan panjang tali yang bisa disetel yang menghubungkan tali bahu ke ransel. Jika tinggi ransel adalah 50 cm dan tali bahu adalah 30 cm, maka panjang tali penghubung yang bisa disetel tidak mungkin sama dengan ....

S4
Bagian depan sebuah meja kantor berbentuk persegi tanpa ornamen. Jika diketahui selisih antara panjang diagonal dan rusuk persegi tersebut adalah 4 cm, maka luas persegi tersebut adalah ....
S5
Sebuah piramida di Mesir bebentuk seperti gambar berikut ini.

Jika satuan panjang dari gambar di atas adalah meter, maka nilai p adalah ....
S6
Anton sedang mendesain sebuah permainan dengan menggunakan sapu lidi. Permainan tersebut dirancang dengan bentuk segitiga seperti tampak pada gambar berikut ini.

Jika ukuran panjang dalam gambar di atas adalah cm, maka panjang sapu lidi yang dibutuhkan Anton untuk mendesain permainan tersebut adalah ....
S7
Sebuah segitiga ABC dengan AB = 5 cm, BC = 6 cm, dan AC = 7 cm. Jika AD adalah garis tinggi sedemikian hingga titik D pada BC, maka luas segitiga ABC adalah ....
S8
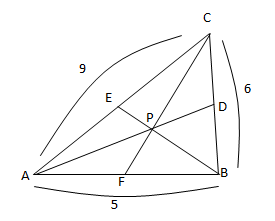
Seorang arsitek memodelkan bagian atas sebuah rumah jika dilihat dari depan yang terlihat bebentuk segitiga seperti ilustrasi berikut ini.

Dalam model tersebut, AB = 6 cm, AC = 8 cm, dan BC = 8 cm. Jika D terletak pada AC dengan AD = 5 cm, E pada BC dengan BE = 3 cm, makap anjang AE adalah ....
S9
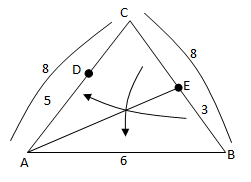
Sebuah perusahaan mainan hendak meluncurkan rubiks cube dengan permukaan berbentuk segitiga sesuai dengan ilustrasi berikut :

Jika AB = 5 cm, AC = 9 cm, BC = 6 cm, dan garis berat AD dan BE berpotongan di titik P, maka [anjang AD adalah ....
S10
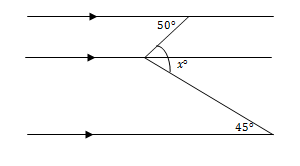
Sebuah alat eksperimen fisika bernama BIASQ1 digunakan untuk membiaskan benda yang dimasukkan ke kolam mulai pada kedalaman tertentu. Jika sebuah tongkat dimasukkan ke dalam kolam sudut 500 dari permukaan dan BIASQ1 membiaskan tongkat tersebut seperti ilustrasi berikut, maka besar sudut pembiasan adalah ....

