Contoh Soal Menggunakan definisi geometris 2

Contoh Soal Menggunakan definisi geometris 2 - Rotasi

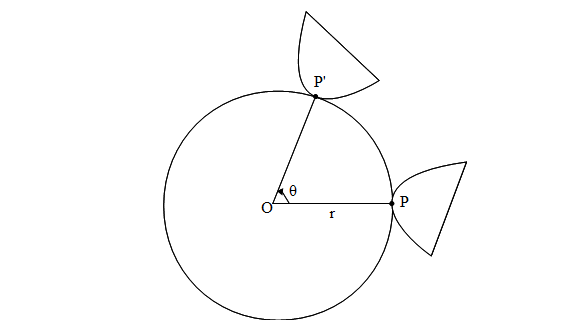
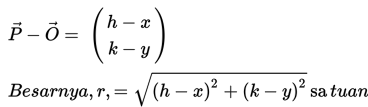
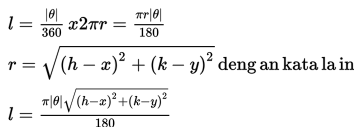
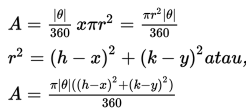
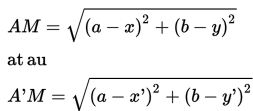
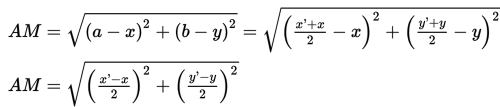
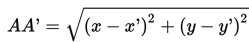
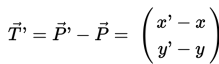
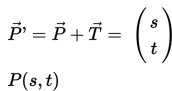
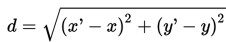
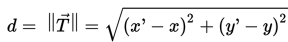
Karena rotasi adalah gerakan yang melalui busur lingkaran, dapat kita misalkan  pusat of rotasi,( pusat lingkaran) adalah O(x,y) dan titik yang dirotasikan adalah P(h,k) maka

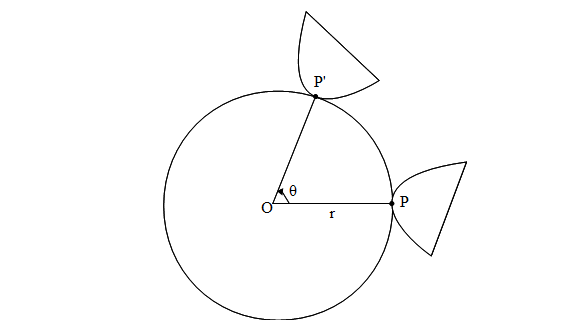
1. Jarak bayangan ke titik pusat = Jarak objek ke titik pusat, besarnya adalah panjang ruas garis OP.

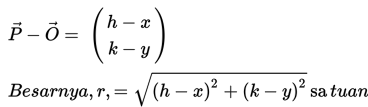
1. Jika objek P bergerak dari titik P ke titik P' sebesar sudut tertentu, 
       theta, maka besar perpindahannya  sama dengan panjang busur PP' yang 
       jari-jarinya r seperti pada persamaan di atas. Kita ambil nilai mutlak dari theta karena theta  
       nilainya bisa positif ataupun negatif.Panjang busur adalah pecahan dari  
       keliling lingkaran dan dapat diperoleh dengan cara seperti berikut ini 

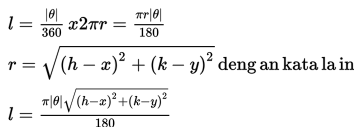
1. Luas area yang dibentuk oleh pergerakan objek, r, adalah luas dari bidang 
       PP'O yang mana merupakan  bagian dari luas lingkaran. Dapat ditulis

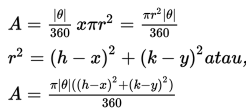
Refleksi

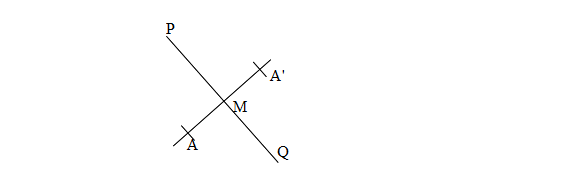
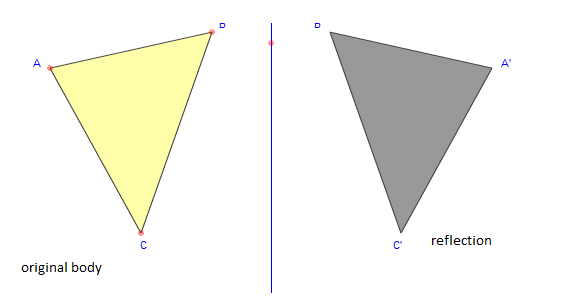
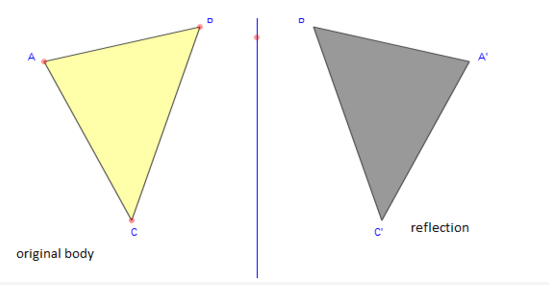
Perhatikan objek A(x,y) dipetakan ke A'(x',y') dengan garis PQ sebagai cermin. 

1. Karena jarak objek ke cermin = jarak bayangan ke cermin, titik potong M adalah 

    titik tengah dari garis AA' seperti berikut ini

Jarak terpendek antara bayangan dengan garis cermin sama dengan jarak terpendek antara objek dengan garis cermin.  Jarak ini sama dengan AM = A'M. Dapat ditulis seperti berikut ini

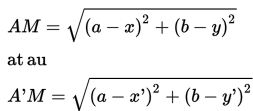
Ambil persamaan pertama, kita peroleh

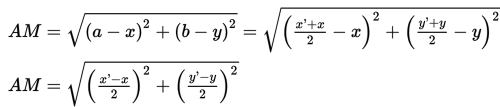
Jarak antara dua titik (objek dan bayangan) adalah 2AM, atau  

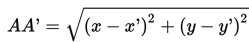
Translasi

Pada saat sebuah titik ditranslasikan dari P(x,y) ke P'(x,y), vektor yang mendeskripsikan hal itu disebut vektor  translasi . 

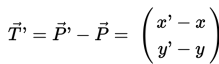
Ketika diberikan vektor translasi dan koordinat objek yang akan ditranslasikan, bayangannya dapat diperoleh dengan cara sebagai berikut

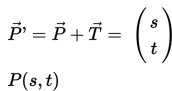
Besarnya perpindahan objek  translasi  adalah jarak pergeseran titik P ke P', yaitu

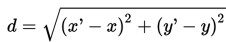
Tapi jarak pergeseran sama dengan modulus vektor translasi T. Dengan demikian  jaraknya, d, yang merupakan besar dari perpindahan objek yang ditranslasikan, adalah modulus dari vektor translasi, T. Thus 

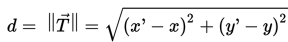
S1

Suatu komidi putar (merry-go-round) berputar dua kali terhadap pusat putarannya, berapa derajat kah sudut yang dibentuk dari dua putaran?

S2

Planet bumi .......... terhadap sumbu rotasinya sendiri, sekaligus berputar mengitari matahari.

S3

Suatu translasi adalah transformasi yang ..................

S4

Bumi berputar pada sumbunya dalam satu hari. Jika bumi berputar selama dua belas jam, berapakah sudut yang terbentuk?

S5

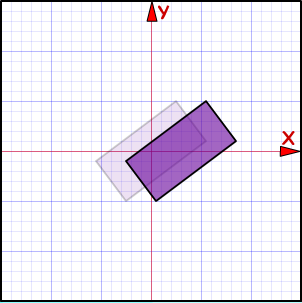
Pada gambar di bawah ini, tampak bahwa sebuah kotak di bidang-xy ditranslasikan sejauh 30 satuan. Berapakah sudut translasinya?

S6

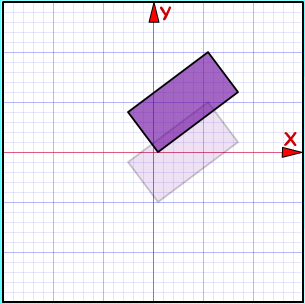
Pada gambar di bawah ini, suatu benda ditranslasikan sejauh 50 satuan. Bagaimanakah arah translasinya?

S7

Penggal garis yang menghubungkan suatu benda dan hasil pencerminannya memotong sumbu pencerminan pada .............?

S8

Penggal garis yang menghubungkan suatu titik dengan bayangannya yang bersesuaian saling ............ satu dengan yang lainnya.

S9

Manakah dari transformasi berikut ini yang mengakibatkan suatu segitiga menjadi tidak kongruen lagi?

S10

Apa yang bisa dikatakan tentang jarak suatu titik dengan sumbu pencerminan dengan jarak bayangan titik tersebut dengan sumbu pencerminannya?

Share this post