Contoh Soal Sifat-sifat Persamaan trigonometri
Contoh Soal Sifat-sifat Persamaan trigonometri - Gunakan pengetahuan kalian akan materi tersebut, sehingga kalian dapat dengan mudah memahami materi sifat-sifat trigonometri ini.
Persamaan Identitas Trigonometri
Contoh 1 :
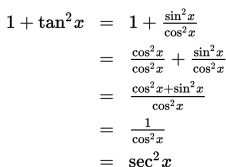
Contoh 2 :
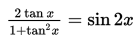
Penyelesaian :
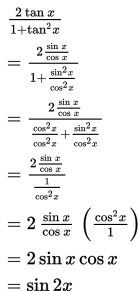
Persamaan Trigonometri Sederhana
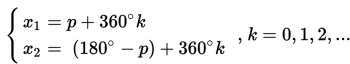
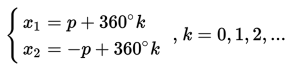
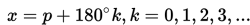
Contoh 3:
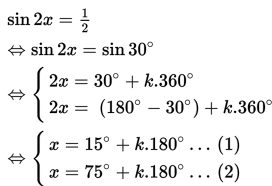
Contoh 4 :
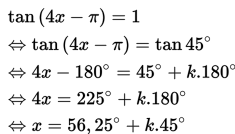
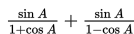
Persamaan Identitas Trigonometri
Persamaan identitas trigonometri yang paling sering digunakan adalah sebagai berikut :
- cos2 x + sin2 x = 1
- 1 + tan2 x = sec2 x
- 1 + cot2 x = cosec2 x
Contoh 1 :
Buktikan identitas trigonometri 1 + tan2 x = sec2 x !
Penyelesaian :
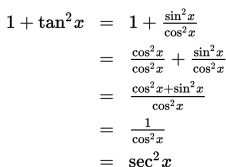
(terbukti)
Contoh 2 :
Buktikan identitas trigonometri berikut!
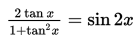
Penyelesaian :
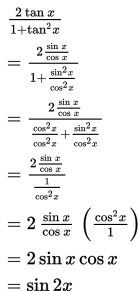
(terbukti)
Persamaan Trigonometri Sederhana
Sifat-sifat persamaan trigonometri sederhana untuk sinus, cosinus, dan tangen adalah sebagai berikut :
1. Bentuk sin x = sin p
Bentuk di atas mempunyai dua macam penyelesaian, yaitu :
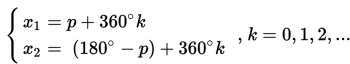
2. Bentuk cos x = cos p
Bentuk di atas mempunyai dua macam penyelesaian, yaitu :
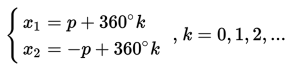
3. Bentuk tan x = cos p
Bentuk di atas mempunyai penyelesaian sebagai berikut :
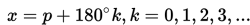
Contoh 3:
Tentukan himpunan penyelesaian dari sin 2x = ½ jika 0∘ ≤ x ≤ 360∘ !
Penyelesaian :
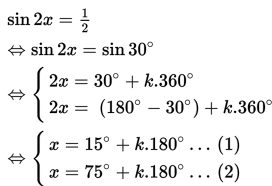
Persamaan (1)
- Jika k = 0 maka x1 = 15o
- Jika k = 1 maka x2 = 195o
Persamaan (2)
- Jika k = 0 maka x3 = 75o
- Jika k = 1 maka x4 = 255o
Jadi, himpunan penyelesaiannya adalah {15o, 75o, 195o, 255o}.
Contoh 4 :
Tentukan himpunan penyelesaian dari tan (4x - π) = 1 !
Penyelesaian :
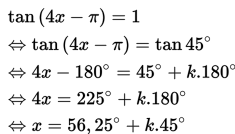
- Jika k = 0 maka x1 = 56,25∘
- Jika k = 1 maka x2 = 101,25∘
- Jika k = 2 maka x3 = 146,25∘
- Jika k = 3 maka x4 = 191,25∘
- Jika k = 4 maka x5 = 236,25∘
- Jika k = 5 maka x6 = 281,25∘
- Jika k = 6 maka x7 = 326,25∘
- Jika k = 7 maka x8 = 371,25∘ = 11,25∘
Jadi, himpunan penyelesaiannya adalah
{ 11,25∘ , 56,25∘ , 101,25∘ , 146,25∘ , 191,25∘ , 236,25∘ , 281,25∘ , 326,25∘ }.
{ 11,25∘ , 56,25∘ , 101,25∘ , 146,25∘ , 191,25∘ , 236,25∘ , 281,25∘ , 326,25∘ }.
S1
Himpunan penyelesaian dari dari 2 sin 2x = √3 pada interval 0o ≤ x ≤ 360o adalah ....
S2
Himpunan penyelesaian dari dari cos 4x = cos 2x pada interval 0o ≤ x ≤ 180o adalah ....
S3
Bentuk sederhana dari
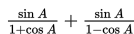
adalah ....
S4
Himpunan penyelesaian dari tan x - √3 = 0 pada interval
0o ≤ x ≤ 90o adalah ....
0o ≤ x ≤ 90o adalah ....
S5
Bentuk sederhana dari (sin B + cos B)2 – (sin B – cos B)2 adalah ....
S6
Himpunan penyelesaian dari cos 3x = cos ( x + 60o ) pada interval 0o ≤ x ≤ 90o adalah ....
S7
Himpunan penyelesaian dari √8 sin x – 2 = 0 pada interval 0o ≤ x ≤ 180o adalah ....
S8
Himpunan penyelesaian dari √3 tan x - √3 = 0 pada interval 0o ≤ x ≤ 360o adalah ....
S9
Pernyataan berikut ini benar, kecuali ....
S10
Himpunan penyelesaian dari sin x = cos 60o pada interval 90o ≤ x ≤ 1800o adalah ....
