Contoh Soal Fungsi Trigonometri dan grafiknya
Contoh Soal Fungsi Trigonometri dan grafiknya - Dalam topik ini kalian akan belajar tentang fungsi trigonometri dan cara menggambar grafiknya. Diharapkan kalian bisa mengingat kembali bagian sudut-sudut istimewa yang telah kalian pelajari di matematika wajib. Mari kita mulai belajar.
Nilai Fungsi Trigonometri
Menggambar Grafik Fungsi Trigonometri
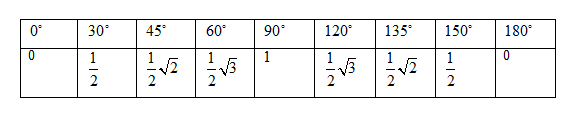

Menentukan Persamaan Grafik Fungsi Trigonometri
x ) = 2 cos x + sin x tan 2 x
untuk x = π/3 adalah ....
Nilai Fungsi Trigonometri
Menentukan nilai fungsi trigonometri dengan cara mensubtitusikan nilai variabel yang diberikan ke dalam fungsi.
Contoh : Tentukan nilai fungsi dari f(x) = 2(sin 2x), jika x = 15o !
Penyelesaian :
f(30o) = 2 (sin 2(15o)) = 2 sin 30o = 2(½) = 1.
Menggambar Grafik Fungsi Trigonometri
Langkah-langkah menggambar grafik fungsi trigonometri :
a. Melengkapi tabel sudut-sudut istimewa
b. Menentukan titik pada bidang kartesius
c. Menghubungkan titik-titik sehingga terbentuk kurva
a. Melengkapi tabel sudut-sudut istimewa
b. Menentukan titik pada bidang kartesius
c. Menghubungkan titik-titik sehingga terbentuk kurva
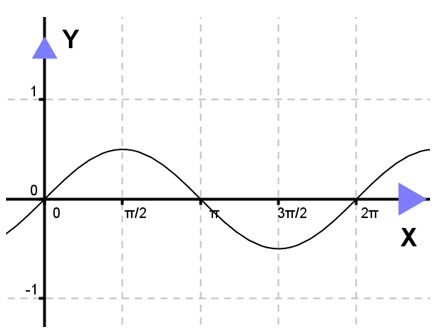
Contoh : Gambarkan grafik fungsi y = sin x !
Penyelesaian :
Jika kita subtitusikan beberapa nilai x ke persamaan y = sin x, maka diperoleh tabel berikut :
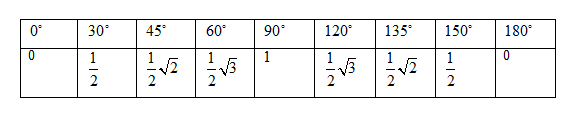
Selanjutnya, jika setiap titik dalam tabel dihubungkan dalam koordinat kartesius, maka diperoleh grafik y = sin x sebagai berikut :

Menentukan Persamaan Grafik Fungsi Trigonometri
Jika kita ingin mengetahui persamaan dari grafik fungsi trigonometri, kita harus mengingat kembali bentuk umum persamaan trigonometri, yaitu f(x) = A sin k(x – a), dimana
- A = amplitudo (nilai maksimum)
- k = 2π/p
- p = periode grafik
- a = absis titik awal grafik
Mari kita perhatikan kembali grafik y = sin x. Nilai maksimumnya adalah 1 dan grafik berulang setelah 3600. Dengan demikian, A = 1 dan p = 2π.
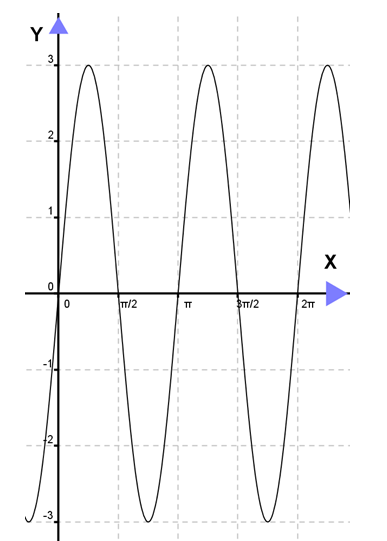
Contoh : Tentukan persamaan grafik dibawah ini!

Grafik di atas adalah grafik fungsi sinus. Dengan demikian, bentuk umumnya adalah
f(x) = A sin k(x – a).
f(x) = A sin k(x – a).
Oleh karena absis awal dari grafik di atas adalah nol, nilai maksimum fungsi adalah 3 dan grafik fungsi berulang setelah 1800, maka
- a = 0
- A = 3
- p = π
- k = 2π/π = 2
Jadi persamaan grafik fungsi di atas adalah f(x) = 3(sin 2x).
S1
Nilai f(x) = 2 sin x + cos x untuk x = π/4 adalah ....
S2
Diketahui f(x) = a cos x + b sin x.
Jika f(π) = -2 dan f(π/2) = 3, maka 3a + b adalah ....
Jika f(π) = -2 dan f(π/2) = 3, maka 3a + b adalah ....
S3
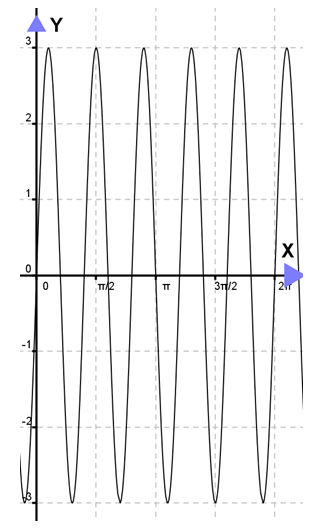
Grafik fungsi untuk y = sin 4x adalah ....
S4
Amplitudo dari persamaan y = 5 sin (2x – π) adalah ....
S5
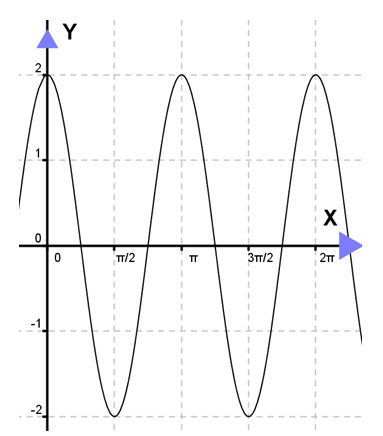
Persamaan grafik di bawah ini adalah ....

S6
Nilai fungsi
untuk x = π/3 adalah ....
S7
Pernyataan berikut ini benar, kecuali ....

S8
Nilai maksimum dari f(x) = 3 + 2 sin x adalah ....
S9
Nilai minimum f(x) = -cos x – 4 sin x adalah ....
S10
Persamaan grafik yang memiliki amplitudo yang sama dengan grafik di bawah ini adalah ....

