Contoh Soal Persamaan Trigonometri
Contoh Soal Persamaan Trigonometri - Dalam topik ini, kalian akan belajar tentang persamaan trigonometri. Pada topik sebelumnya, kalian telah mempelajari materi sifat-sifat persamaan trigonometri yang akan membantu kalian mempelajari topik ini. Mari kita mulai!
Persamaan Trigometri a cos x + b sin x = c
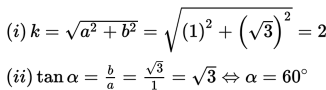
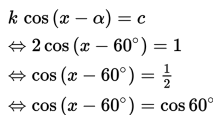
Penyelesaiannya adalah
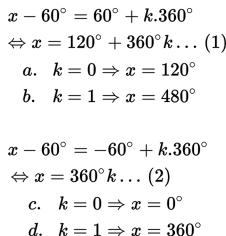
Persamaan Trigonometri a(p)^2 + b(p) + c = 0, dengan p = sin x, atau p = cos x, atau p = tan x
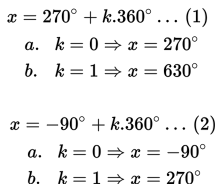
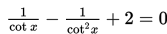
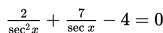
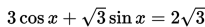
Persamaan Trigometri a cos x + b sin x = c
Persamaan ini dapat diselesaikan dengan cara mengubahnya ke bentuk k cos (x – α) = c, dengan
- k2 =a2 + b2
- α = arc tan b/a
- c2 ≤ a2 + b2
Contoh :
Tentukan himpunan penyelesaian dari persamaan cos x + √3 sin x = 1 jika 0o ≤ x ≤ 360o !
Penyelesaian :
cos x + √3 sin x = 1 => a = 1, b = √3, c = 1
Dengan demikian,
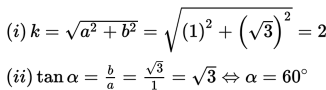
Jika cos x + √3 sin x = 1 diubah ke dalam bentuk k cos (x – α) = c, maka diperoleh hasil sebagai berikut :
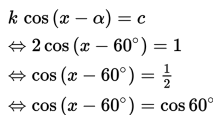
Penyelesaiannya adalah
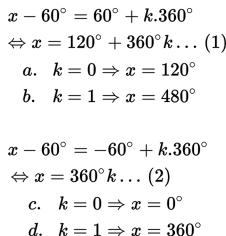
Berdasarkan uraian di atas, himpunan penyelesaian dari persamaan cos x + √3 sin x = 1 jika 0o ≤ x ≤ 360o adalah {0o, 120o, 360o}.
Persamaan Trigonometri a(p)^2 + b(p) + c = 0, dengan p = sin x, atau p = cos x, atau p = tan x
Persamaan trigonometri berbentuk a(p)2 + b(p) + c = 0 dapat diselesaikan dengan cara menyelesaikan persamaan kuadratnya.
Contoh :
Tentukan himpunan penyelesaian dari persamaan sin2 x – sin x – 2 = 0 jika 0o ≤ x ≤ 360o !
Penyelesaian :
Jika dimisalkan p = sin x, maka persamaan menjadi p2 – p – 2 = 0.
Selanjutnya, jika persamaan di atas kita faktorkan, maka diperoleh hasil sebagai berikut :
p2 – p – 2 = 0
<=> (p – 2)(p + 1) = 0
<=> p = 2 atau p = -1
<=> (p – 2)(p + 1) = 0
<=> p = 2 atau p = -1
Selanjutnya, karena -1 ≤ sin x ≤ 1 , maka nilai yang mungkin hanya untuk p = -1.
p = -1
<=> sin x = -1
<=> sin x = sin 270o
<=> sin x = -1
<=> sin x = sin 270o
Penyelesaiannya adalah
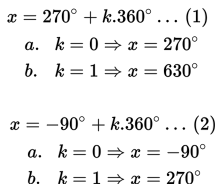
Berdasarkan uraian di atas, himpunan penyelesaian dari persamaan sin2 x – sin x – 2 = 0 jika 0o ≤ x ≤ 360o adalah {270o}
S1
Himpunan penyelesaian dari persamaan
2 cos x – sin2 x – 2 = 0 dengan 360o > x ≥ 0o adalah ....
2 cos x – sin2 x – 2 = 0 dengan 360o > x ≥ 0o adalah ....
S2
Himpunan penyelesaian dari persamaan
cos2 x + cos x – 2 = 0 dengan 360o ≥ x ≥ 0o adalah ..
cos2 x + cos x – 2 = 0 dengan 360o ≥ x ≥ 0o adalah ..
S3
Himpunan penyelesaian dari persamaan cos x + sin x = -1 jika 0∘ ≤ x ≤ 360∘ adalah ....
S4
Himpunan penyelesaian dari persamaan
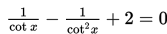
dengan 360o ≥ x ≥ 0o adalah ....
S5
Himpunan penyelesaian dari persamaan tan2 x – 1 = 0 untuk 0∘ ≤ x ≤ 360∘ adalah ....
S6
Jika 0∘ ≤ x ≤ 90∘ , maka himpunan penyelesaian dari persamaan berikut ini adalah ….
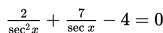
S7
Syarat agar persamaan q sin2 x – p = 0 memiliki penyelesaian adalah ....
S8
Jika (sin x + cos x)2 = 1 maka pernyataan yang benar adalah ....
S9
Himpunan penyelesaian dari persamaan
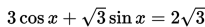
jika 0∘ < x < 90∘ adalah...
S10
Diberikan persamaan trigonometri
p sin2 x + p cos2 x – cos2 x = 0
Jika salah satu penyelesaiannya adalah x = 180o dan
p > 0, maka nilai p yang mungkin adalah ....
p sin2 x + p cos2 x – cos2 x = 0
Jika salah satu penyelesaiannya adalah x = 180o dan
p > 0, maka nilai p yang mungkin adalah ....
