Contoh Soal Identitas Trigonometri
Contoh Soal Identitas Trigonometri - Dalam topik ini kalian akan belajar mengenai identitas trigonometri. Namun sebelumnya mari kita ingat kembali beberapa rumus dasar dan sifat trigonometri.
Perbandingan Trigonometri Pada Segitiga Siku-Siku
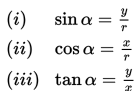
Perbandingan Trigonometri di Berbagai Kuadran
Sudut-Sudut Istimewa
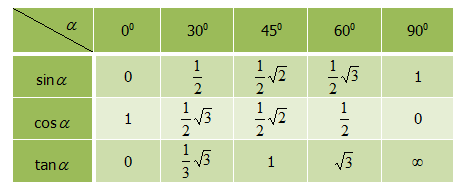
Grafik Fungsi Trigonometri
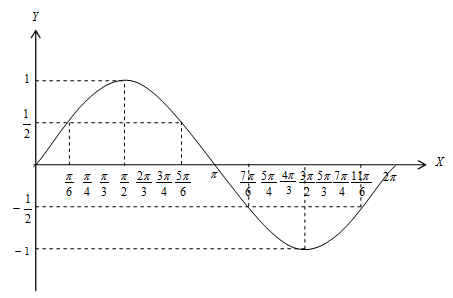
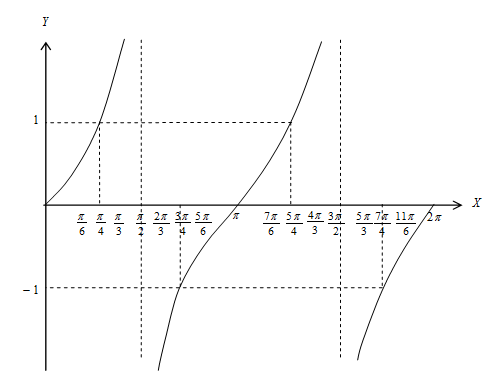
Apakah kalian sudah mulai ingat kembali?
Identitas Trigonometri

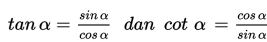
c. Identitas Pythagoras
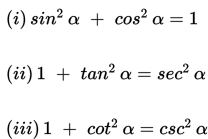
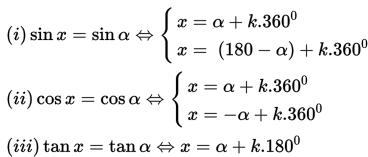
Untuk memperdalam pemahaman kalian mengenai identitas trigonometri, mari kita cermati beberapa contoh soal berikut ini.


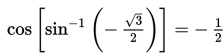
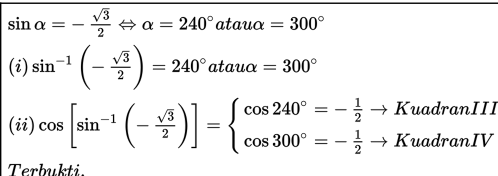

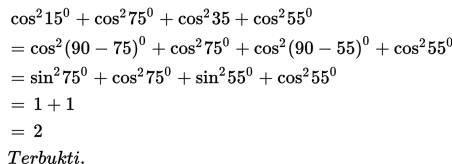
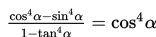

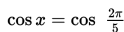
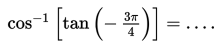
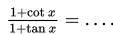
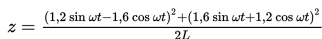
Perbandingan Trigonometri Pada Segitiga Siku-Siku
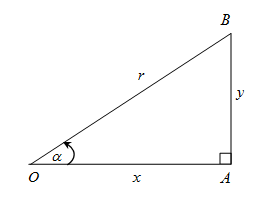
Dalam segitiga siku-siku di bawah ini, berlaku :

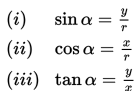
Dalam segitiga siku-siku kita mengenal teorema Pythagoras yang menyatakan bahwa “kuadrat sisi miring (hipotenusa) merupakan jumlah kuadrat dari dua sisi penyikunya”.
Secara matematis, teorema Pythagoras adalah x2 + y2 = r2.
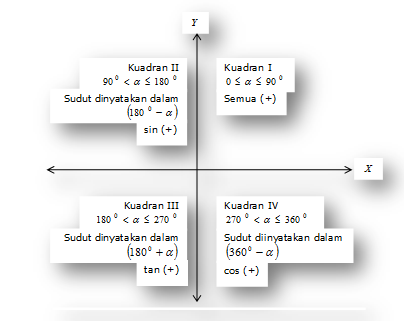
Perbandingan Trigonometri di Berbagai Kuadran
Nilai sinus, cosinus, dan tangen suatu sudut ditentukan oleh besar sudut tersebut. Gambar berikut ini mengilustrasikan nilai dari sinus, cosinus, dan tangen dalam setiap kuadran dan besar sudut dalam setiap kuadran.

Sudut-Sudut Istimewa
Berikut ini adalah tabel nilai sinus, cosinus, dan tangen dari sudut-sudut istimewa :
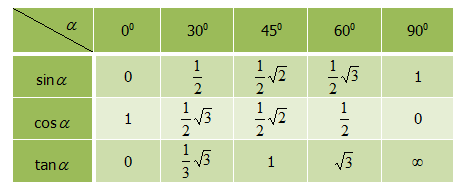
Grafik Fungsi Trigonometri
Grafik fungsi sinus → f(x) = sin x
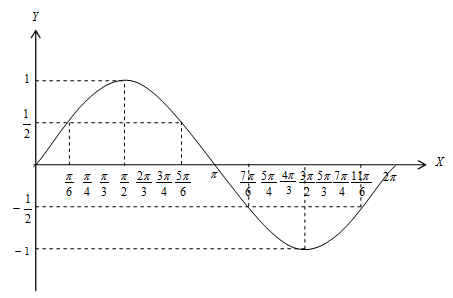
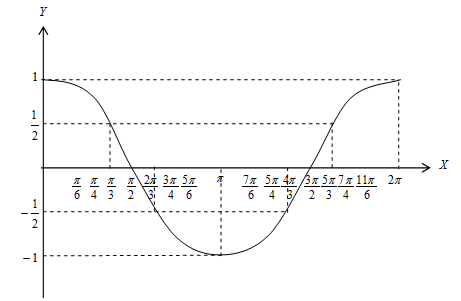
Grafik fungsi cosinus → f(x) = cos x

Grafik fungsi tangen → f(x) = tan x
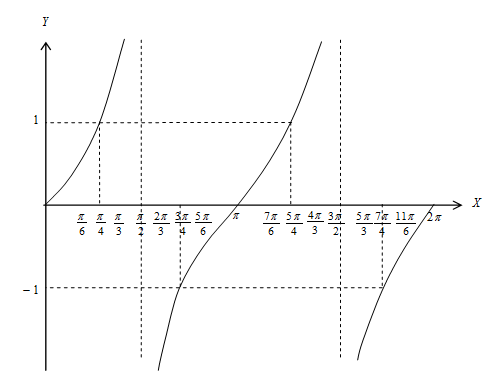
Apakah kalian sudah mulai ingat kembali?
Identitas Trigonometri
Identitas trigonometri atau kesamaan trigonometri adalah identitas atau kesamaan yang memuat perbandingan trigonometri suatu sudut. Sebuah Identitas trigonometri dapat ditunjukan kebenarannya dengan cara mengubah salah satu bentuk ruas sehingga diperoleh bentuk yang sama dengan ruas yang lainnya.
Ada beberapa rumus identitas trigonometri yang perlu kita ketahui, yaitu :
a. Identitas Kebalikan

b. Identitas Perbandingan
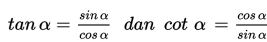
c. Identitas Pythagoras
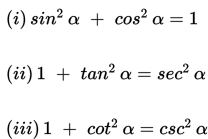
Persamaan Trigonometri
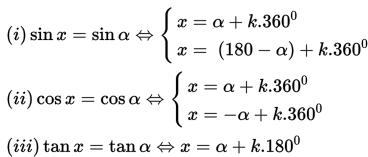
Untuk memperdalam pemahaman kalian mengenai identitas trigonometri, mari kita cermati beberapa contoh soal berikut ini.
Contoh 1 :
Jika x terletak pada interval [0∘ , 360∘], maka tentukan nilai x yang memenuhi persamaan trigonometri sin x = sin 10o !
Penyelesaian :

Contoh 2 :
Tentukan nilai x yang memenuhi persamaan 2 cos x = √3 jika x terletak pada interval [0, 360∘] !
Penyelesaian :

Contoh 3 :
Buktikan bahwa
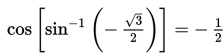
Penyelesaian :
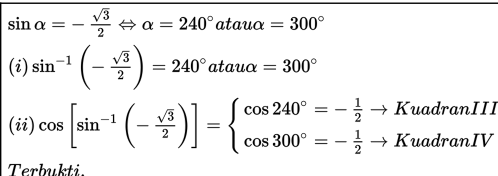
Contoh 4 :
Buktikan identitas trigonometri berikut :

Penyelesaian :
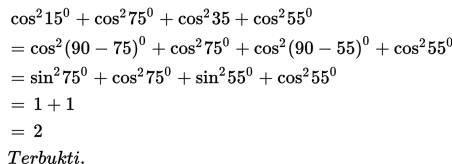
Contoh 5 :
Buktikan identitas trigonometri berikut :
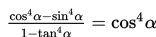
Penyelesaian :

S1
Jika x terletak dalam interval [0 , 2π], maka nilai x yang memenuhi persamaan berikut ini adalah ....
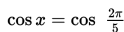
S2
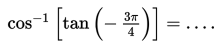
S3
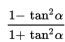
S4
Nilai x yang memenuhi persamaan
2 sin2 2x – 7 sin 2x + 3 = 0 untuk 0o < x < 360o adalah ....
2 sin2 2x – 7 sin 2x + 3 = 0 untuk 0o < x < 360o adalah ....
S5
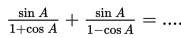
S6
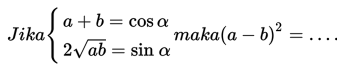
S7
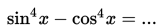
S8
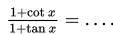
S9
Hukum Malus berkaitan dengan sinar yang datang pada suatu keping polarisator dengan sudut datang ϴ dan intensitas maksimum sinar yang diteruskan adalah M. Hukum Malus dinyatakan dengan
I = M – M tan2 ϴ cos2 ϴ.
I = M – M tan2 ϴ cos2 ϴ.
Nilai sin ϴ dari penjabaran rumus di atas adalah ....
S10
Dalam teori rangkaian listrik, terdapat suatu tetapan yang dirumuskan sebagai berikut :
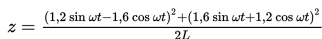
Nilai z sama dengan ….
