Contoh Soal Penerapan pada masalah matematika tentang pertidaksamaan Pecahan
Contoh Soal Penerapan pada masalah matematika tentang pertidaksamaan Pecahan - Kita akan membahas dua macam pertidaksamaan pecahan, yaitu pertidaksamaan pecahan bentuk linear dan pertidaksamaan pecahan bentuk kuadrat.
Pertidaksamaan pecahan bentuk linear :
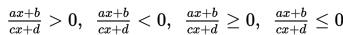
Pertidaksamaan pecahan bentuk kuadrat :
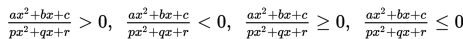
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
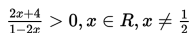
Penyelesaian :
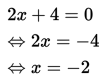
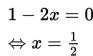

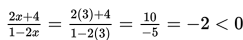
Contoh 2 :
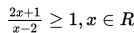
Penyelesaian :
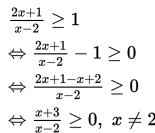
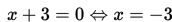
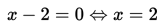
Contoh 3 :
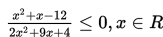
Penyelesaian :
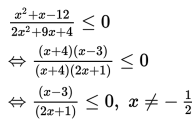
Contoh 4 :
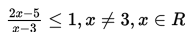
Penyelesaian :
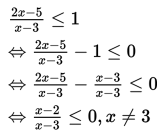
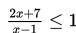
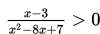
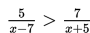
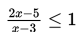
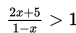
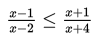
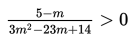
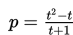
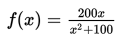
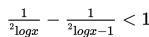
Pertidaksamaan pecahan adalah pertidaksamaan yang mempunyai bentuk pecahan dan mengandung variabel x pada penyebutnya.
Pertidaksamaan pecahan bentuk linear :
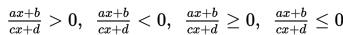
dengan a, b, c, d ∈ R dan cx + d ≠ 0
Pertidaksamaan pecahan bentuk kuadrat :
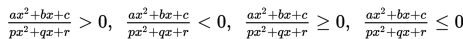
dengan a, b, c, p, q, r ∈ R dan px2 + qx + r ≠ 0
Langkah-langkah penyelesaian pertidaksamaan pecahan adalah sebagai berikut.
a. Tempatkanlah pembuat nol yang diperoleh dari pembilang dan penyebut pada suatu garis bilangan.
b. Periksa tanda dari nilai pecahan ini pada tiap interval yang terbentuk.
c. Tentukan himpunan penyelesaian sesuai tanda pertidaksamaannya.
a. Tempatkanlah pembuat nol yang diperoleh dari pembilang dan penyebut pada suatu garis bilangan.
b. Periksa tanda dari nilai pecahan ini pada tiap interval yang terbentuk.
c. Tentukan himpunan penyelesaian sesuai tanda pertidaksamaannya.
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Tentukan himpunan penyelesaian dari pertidaksamaan :
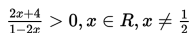
Penyelesaian :
Pembuat nol pembilang:
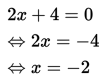
Pembuat nol penyebut:
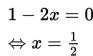
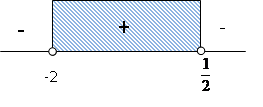
Ada 3 interval yang dipisahkan oleh :
(i) x = -2
(ii) x = ½
(i) x = -2
(ii) x = ½

Jika x = 3, maka
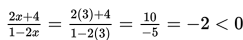
Jadi, pada interval paling kanan yaitu, x > 1/2 tandanya – (negatif).
Selanjutnya, dengan memilih x = 0 (terletak pada interval) -2 < x < 2 dan x = -3, diperoleh hasil sebagai berikut :

Jadi himpunan penyelesaiannya adalah {x | -2 < x < ½}
Contoh 2 :
Tentukanlah himpunan penyelesaian dari pertidaksamaan
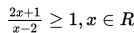
Penyelesaian :
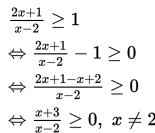
Pembuat nol pembilang:
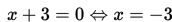
Pembuat nol penyebut:
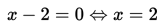

Jadi himpunan penyelesaiannya adalah {x | x ≤ -3 atau x > 2, x ∈ ℝ}
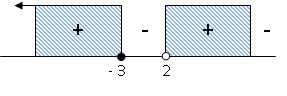
Contoh 3 :
Tentukanlah himpunan penyelesaian dari pertidaksamaan
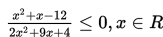
Penyelesaian :
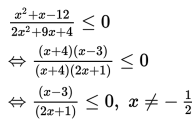
Pembuat nol pembilang dan penyebut berturut-turut adalah 3 dan - 1/2.
Jadi, himpunan penyelesaian adalah {x | -½ < x ≤ 3, x ∈ ℝ}
Contoh 4 :
Tentukan himpunan penyelesaian pertidaksamaan
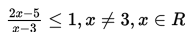
Penyelesaian :
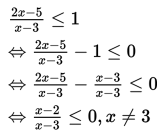
Pembuat nol pembilang dan penyebut berturut-turut adalah 2 dan 3.
Jadi, himpunan penyelesaian adalah {x | 2 ≤ x < 3, x ∈ ℝ}
S1
Pertidaksamaan
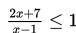
dipenuhi oleh ...
S2
Diberikan pertidaksamaan
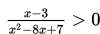
Himpunan penyelesaian pertidaksamaan tersebut adalah ...
S3
Diketahui pertidaksamaan
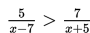
Himpunan penyelesaian pertidaksamaan tersebut adalah ...
S4
Pertidaksamaan
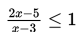
dipenuhi oleh ...
S5
Pertidaksamaan
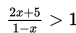
dipenuhi oleh ...
S6
Diberikan pertidaksamaan
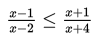
Himpunan penyelesaian pertidaksamaan tersebut adalah ...
S7
Nilai yang memenuhi pertidaksamaan
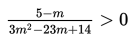
adalah ...
S8
Ketika suatu software baru diluncurkan di pasar, penjualan mingguan umumnya meningkat secara cepat dalam suatu periode tertentu. Selanjutnya penjualan mingguan mulai menurun. Anggap penjualan mingguan software tersebut minggu setelah diperkenalkan bisa dinyatakan oleh
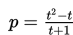
dengan p dalam ribuan. Nilai t yang memenuhi agar software wajib ada yang terjual adalah ...
S9
Populasi kelinci pada suatu pulau setiap tahun dimodelkan sebagai
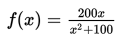
dengan x adalah lamanya waktu populasi kelinci dalam satu tahun. Waktu yang diperlukan agar populasi kelinci mencapai 800 ekor atau lebih per tahun adalah ...
S10
Nilai x yang memenuhi
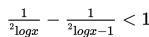
adalah ...
