Invers Matriks 3 x 3
Invers Matriks 3 x 3 - Halo, apa kabar? Masih semangat belajar matematika bukan?
Apakah kalian tahu sebabnya?
Masih ingatkah kalian?
Contoh 1:
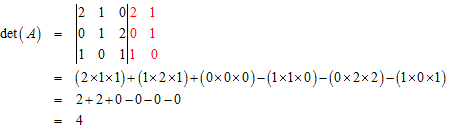
Contoh 2:
Contoh 3:
Contoh 4:
Tentunya sekarang kalian sudah paham mengenai bagaimana menentukan invers dari suatu matriks bukan?
 |
| Invers Matriks 3 x 3 |
Pada topik sebelumnya kalian telah belajar tentang invers matriks berordo 2 x 2. Nah, pada topik kali ini kita akan belajar tentang invers matriks berordo 3 x 3.
Invers matriks A berordo 3 x 3 dapat ditentukan dengan menggunakan rumus: , dimana Adj (A) adalah adjoint dari matriks A.
Rumus di atas mengisyaratkan bahwa matriks A akan memiliki invers jika dan hanya jika determinannya tidak bernilai nol.
Apakah kalian tahu sebabnya?
Ya, sebab jika determinan matriks A adalah nol, maka hasil bagi antara Adj (A) dan determinan A menjadi tidak terdefinisi.
Perlu kalian ketahui, untuk menentukan invers suatu matriks yang berordo 3 x 3, kalian perlu menentukan terlebih dahulu nilai dari determinan, minor, kofaktor, dan adjoint dari matriks tersebut.
Keempat hal tersebut telah kalian pelajari pada topik-topik sebelumnya.
Masih ingatkah kalian?
Oke, mari kita ulas kembali materi tentang determinan, minor, kofaktor, dan adjoint.
Determinan
Seperti yang telah kalian pelajari sebelumnya, determinan matriks berordo 3 x 3 dapat ditentukan dengan menggunakan kaidah Sarrus.
Contoh 1:
Diberikan matriks .
Berdasarkan kaidah Sarrus, determinan matriks A adalah
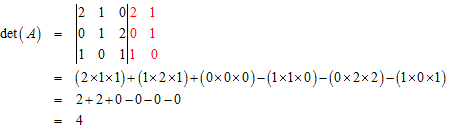
Minor
Apabila elemen baris ke-i dan kolom ke-j dari matriks A berordo 3 x 3 dihilangkan, maka akan diperoleh suatu matriks berordo 2 x 2. Nah, determinan dari matriks berordo 2 x 2 itulah yang selanjutnya disebut dengan minor dari elemen baris ke-i dan kolom ke-j, ditulis dengan simbol Mij.
Contoh 2:
Berdasarkan contoh 1, minor dari setiap elemen pada matriks A adalah sebagai berikut:
Dengan demikian, minor dari matriks A adalah .
Kofaktor
Kofaktor dari elemen baris ke-i dan kolom ke-j dari suatu matriks disimbolkan denganKij dan ditentukan dengan menggunakan rumus: .
Contoh 3:
Berdasarkan contoh 1 dan 2, kofaktor dari elemen-elemen pada matriks A adalah sebagai berikut:
Dengan demikian, kofaktor dari matriks A adalah .
Adjoint
Adjoint suatu matriks adalah transpos dari matriks kofaktornya.
Contoh 4:
Berdasarkan contoh 1 dan 3, adjoint dari matriks A adalah
Invers Matriks
Nah, karena nilai determinan dan adjoint dari matriks A sudah diketahui, maka invers dari matriks A adalah sebagai berikut:
Tentunya sekarang kalian sudah paham mengenai bagaimana menentukan invers dari suatu matriks bukan?
Ayo kerjakan latihan soal dalam topik ini.