Determinan Matriks 3 x 3 dan Sifat-Sifatnya

Determinan Matriks 3 x 3 dan Sifat-Sifatnya - Halo adik-adik, masih semangat belajar matematika bukan?

Determinan Matriks 3 x 3 dan Sifat-Sifatnya

Dalam topik sebelumnya kalian telah belajar mengenai minor dan kofaktor matriks berordo 3 x 3. Nah, pada topik ini kalian akan menggunakan kedua materi tersebut dalam menentukan determinan matriks berordo 3 x 3.

Ada dua cara yang dapat kalian gunakan dalam menghitung determinan matriks 3 x 3, yaitu ekspansi kofaktor dan kaidah Sarrus.

Ekspansi Kofaktor

Dalam menentukan determinan suatu matriks, kalian dapat menggunakan ekspansi kofaktor pada baris ke-i maupun ekspansi kofaktor pada kolom ke-j, dimana i,j = 1, 2, 3.

Perlu kalian ketahui, apapun ekspansi kofaktor yang kalian gunakan, selama perhitungan kalian benar, maka nilai determinan yang diperoleh adalah sama.

Nah, ekspansi kofaktor pada baris ke-i untuk matriks berordo 3 x 3 adalah ai1Ki1 + ai2Ki2+ ai3Ki3 .

Adapun ekspansi kofaktor pada kolom j untuk matriks berordo 3 x 3 adalah a1jK1j + a2jK2j + a3jK3j .

Perlu kalian ingat, aij adalah elemen baris ke-i kolom ke-j dan Kij adalah kofaktor dari elemen aij.

Contoh 1:

Tentukan determinan dari matriks A=⎛⎝⎜⎜24−2−3121−14 ⎞⎠⎟⎟$A=\left(\begin{array}{ccc}2& -3& 1\\ 4& 1& -1\\ -2& 2& 4\end{array}\right)$ dengan menggunakan ekspansi kofaktor pada baris dan kolom.

Penyelesaian:

Langkah pertama adalah menentukan minor dari matriks A.

• M11=∣∣∣12−14 ∣∣∣=6$M_{11}=\left|\begin{array}{ll}1& -1\\ 2& 4\end{array}\right|=6$
• M12=∣∣∣4−2−14 ∣∣∣=14$M_{12}=\left|\begin{array}{ll}4& -1\\ -2& 4\end{array}\right|=14$
• M13=∣∣∣4−212 ∣∣∣=10$M_{13}=\left|\begin{array}{ll}4& 1\\ -2& 2\end{array}\right|=10$
• M21=∣∣∣−3214 ∣∣∣=−14$M_{21}=\left|\begin{array}{ll}-3& 1\\ 2& 4\end{array}\right|=-14$
• M22=∣∣∣2−214 ∣∣∣=10$M_{22}=\left|\begin{array}{ll}2& 1\\ -2& 4\end{array}\right|=10$
• M23=∣∣∣2−2−32 ∣∣∣=−2$M_{23}=\left|\begin{array}{ll}2& -3\\ -2& 2\end{array}\right|=-2$
• M31=∣∣∣−311−1 ∣∣∣=2$M_{31}=\left|\begin{array}{ll}-3& 1\\ 1& -1\end{array}\right|=2$
• M32=∣∣∣241−1 ∣∣∣=−6$M_{32}=\left|\begin{array}{ll}2& 1\\ 4& -1\end{array}\right|=-6$
• M33=∣∣∣24−31 ∣∣∣=14$M_{33}=\left|\begin{array}{ll}2& -3\\ 4& 1\end{array}\right|=14$

Berdasarkan uraian di atas, minor matriks A adalah M=⎛⎝⎜⎜M11M21M31M12M22M32M13M23M33 ⎞⎠⎟⎟=⎛⎝⎜⎜6−1421410−610−214 ⎞⎠⎟⎟$\mathrm{<br>}$

$M=\left(\begin{array}{ccc}{M}_{11}& M_{12}& M_{13}\\ M_{21}& M_{22}& M_{23}\\ M_{31}& M_{32}& M_{33}\end{array}\right)=\left(\begin{array}{ccc}6& 14& 10\\ -14& 10& -2\\ 2& -6& 14\end{array}\right)$.

Langkah kedua adalah menentukan kofaktor dari matriks A.

K=⎛⎝⎜⎜M11−M21M31−M12M22−M32M13−M23M33 ⎞⎠⎟⎟=⎛⎝⎜⎜6142−1410610214 ⎞⎠⎟⎟$\mathrm{<br>}$

$K=\left(\begin{array}{ccc}{M}_{11}& -M_{12}& M_{13}\\ -M_{21}& M_{22}& -M_{23}\\ M_{31}& -M_{32}& M_{33}\end{array}\right)=\left(\begin{array}{ccc}6& -14& 10\\ 14& 10& 2\\ 2& 6& 14\end{array}\right)$

Ekspansi kofaktor pada baris pertama

a11C11+a12C12+a13C13=2(6)+(−3)(−14)+1(10)=12+42+10=64 $\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{ll}{a}_{11}{C}_{11}+a_{12}{C}_{12}+a_{13}{C}_{13}& =2\left(6\right)+(-3)(-14)+1\left(10\right)\\ & =12+42+10\\ & =64\end{array}$

Ekspansi kofaktor pada baris ke-2

a21C21+a22C22+a23C23=4(14)+1(10)+(−1)(2)=56+10−2=64 $\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{ll}{a}_{21}{C}_{21}+a_{22}{C}_{22}+a_{23}{C}_{23}& =4\left(14\right)+1(10)+(-1)\left(2\right)\\ & =56+10-2\\ & =64\end{array}$

Ekspansi kofaktor pada baris ke-3

a31C31+a32C32+a33C33=−2(2)+2(6)+4(14)=−4+12+56=64 $\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{ll}{a}_{31}{C}_{31}+a_{32}{C}_{32}+a_{33}{C}_{33}& =-2\left(2\right)+2\left(6\right)+4\left(14\right)\\ & =-4+12+56\\ & =64\end{array}$

Ekspansi kofaktor pada kolom pertama

a11C11+a21C21+a31C31=2(6)+4(14)+(−2)(2)=12+56−4=64 $\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{ll}{a}_{11}{C}_{11}+a_{21}{C}_{21}+a_{31}{C}_{31}& =2\left(6\right)+4\left(14\right)+(-2)\left(2\right)\\ & =12+56-4\\ & =64\end{array}$

Ekspansi kofaktor pada kolom ke-2

a12C12+a22C22+a32C32=(−3)(−14)+1(10)+2(6)=42+10+12=64 
$\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{ll}{a}_{12}{C}_{12}+a_{22}{C}_{22}+a_{32}{C}_{32}& =(-3)(-14)+1\left(10\right)+2\left(6\right)\\ & =42+10+12\\ & =64\end{array}$

Ekspansi kofaktor pada kolom ke-3

a13C13+a23C23+a33C33=1(10)+(−1)(2)+4(14)=10−2+56=64 $\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{ll}{a}_{13}{C}_{13}+a_{23}{C}_{23}+a_{33}{C}_{33}& =1\left(10\right)+(-1)\left(2\right)+4\left(14\right)\\ & =10-2+56\\ & =64\end{array}$

Berdasarkan uraian di atas, tampak bahwa semua ekspansi kofaktor memberikan hasil yang sama, yaitu 64. Dengan demikian, determinan dari matriks A adalah 64.

Kaidah Sarrus

Penentuan determinan dengan menggunakan kaidah Sarrus memanfaatkan elemen matriks pada dua kolom pertama.

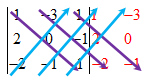
Sebagai contoh, jika kalian ingin menghitung determinan dari matriks A=⎛⎝⎜⎜12−2−30−11−11 ⎞⎠⎟⎟ $A=\left(\begin{array}{ccc}1& -3& 1\\ 2& 0& -1\\ -2& -1& 1\end{array}\right)$, maka kalian perlu menuliskan dua kolom pertama dari matriks A seperti berikut:

det(A)=∣∣∣∣∣12−2−30−11−11 ∣∣∣∣∣12−2−30−1  $det\left(A\right)=\left|\begin{array}{ccc}1& -3& 1\\ 2& 0& -1\\ -2& -1& 1\end{array}\right|\begin{array}{ll}1& -3\\ 2& 0\\ -2& -1\end{array}$

Selanjutnya untuk menentukan determinan, kalikan semua elemen yang dilalui oleh garis yang sama. Nah, determinan adalah hasil pengurangan antara jumlahan nilai dari garis berwarna biru dan jumlahan nilai dari garis berwarna ungu.

det(A)=1(0)(1)+(−3)(−1)(−2)+1(2)(−1)−[−2(0)(−1)+(−1)(−1)(1)+1(2)(−3)]=0−6−2−(0+1−6)=−8+5=−3 $\begin{array}{l}<br>\end{array}$

$\begin{array}{ll}det\left(A\right)& =1\left(0\right)\left(1\right)+(-3)(-1)(-2)+1\left(2\right)(-1)-\left[-2\left(0\right)(-1)+\left(-1\right)(-1)\left(1\right)+1\left(2\right)(-3)\right]\\ & =0-6-2-(0+1-6)\end{array}$

$\begin{array}{ll}& =-8+5\\ & =-3\end{array}$

Sifat Determinan

Pada topik yang telah lalu, kalian telah belajar mengenai sifat-sifat determinan pada matriks berordo 2 x 2.

Apakah ada yang tahu perbedaan antara sifat determinan matriks berordo 2 x 2 dan 3 x 3?

Ya, letak perbedaannya hanya pada determinan hasil perkalian dengan sebuah skalar.

Berikut ini adalah tiga sifat determinan pada matriks berordo 3 x 3:

• det(AT)=det(A)$det(A^T)=det(A)$
• det(AB)=det(A)×det(B)$det(AB)=det(A)\times det(B)$
• det(kA)=k3det(A)

Share this post