Minor dan Kofaktor Matriks 3 x 3

Minor dan Kofaktor Matriks 3 x 3 - Dalam topik kali ini kalian akan belajar mengenai minor dan kofaktor matriks berordo 3 x 3.

Minor dan Kofaktor Matriks 3 x 3

Apakah kalian tahu manfaat mempelajari minor dan kofaktor matriks berordo 3 x 3?

Ya, minor dan kofaktor adalah dua unsur yang sangat bermanfaat dalam menentukan determinan dan invers dari sebuah matriks berordo 3 x 3.

Nah, dalam kehidupan sehari-hari, banyak hal yang dapat dimodelkan dalam persamaan matriks berordo 3 x 3 dan dalam penyelesaiannya kita menggunakan minor dan kofaktor.

Perlu kalian ketahui, sebelum menentukan kofaktor, kalian perlu menentukan minor terlebih dahulu.

Minor

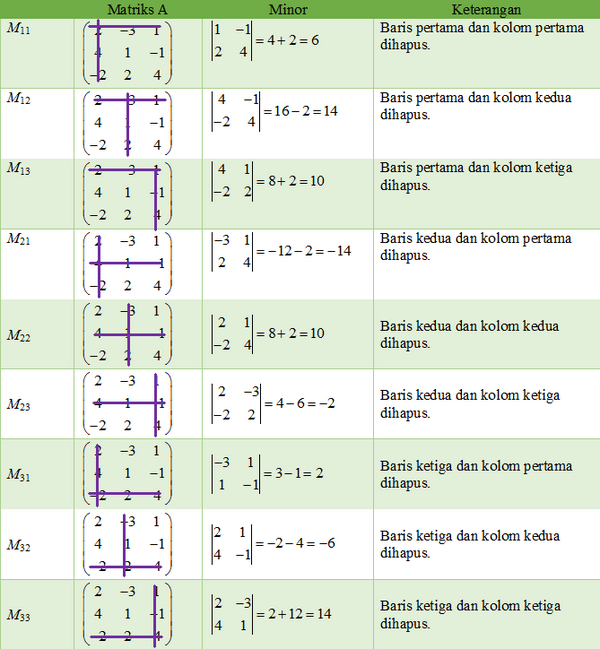
Minor dari elemen aij pada matriks A disimbolkan dengan Mij. Nah, Mij adalah determinan submatriks setelah menghapus baris ke-i dan kolom ke-j dari matriks A.

Yuk kita coba tentukan minor dari matriks A=⎛⎝⎜⎜24−2−3121−14 ⎞⎠⎟⎟$A=\left(\begin{array}{ccc}2& -3& 1\\ 4& 1& -1\\ -2& 2& 4\end{array}\right)$.

Oleh karena matriks A berordo 3 x 3, maka akan ada sembilan elemen pada matriks minornya.

Berdasarkan tabel di atas, dapat kita simpulkan bahwa minor dari matriks A adalah M=⎛⎝⎜⎜M11M21M31M12M22M32M13M23M33 ⎞⎠⎟⎟=⎛⎝⎜⎜6−1421410−610−214 ⎞⎠⎟⎟$\mathrm{<br>}$

$M=\left(\begin{array}{ccc}{M}_{11}& M_{12}& M_{13}\\ M_{21}& M_{22}& M_{23}\\ M_{31}& M_{32}& M_{33}\end{array}\right)=\left(\begin{array}{ccc}6& 14& 10\\ -14& 10& -2\\ 2& -6& 14\end{array}\right)$.

Ingat, menentukan minor memang mudah, tetapi kalian harus teliti.

Kofaktor

Lalu bagaimanakah cara menentukan kofaktor?

Kofaktor dari elemen aij pada matriks A dinotasikan dengan Kij. Nah, Kij diperoleh dengan cara mengalikan minor dari elemen aij dengan (-1)i+j.

Dengan demikian, rumus untuk menentukan kofaktor dari elemen aij adalah Kij=(−1)i+j×Mij$K_{ij}=(-1{)}^{i+j}\times M_{ij}$.

Yuk kita coba tentukan kofaktor dari matriks A=⎛⎝⎜⎜24−2−3121−14 ⎞⎠⎟⎟$A=\left(\begin{array}{ccc}2& -3& 1\\ 4& 1& -1\\ -2& 2& 4\end{array}\right)$.

Perlu kalian ketahui, dalam menentukan kofaktor dari matriks A di atas, kita akan menggunakan minor dari pembahasan sebelumnya.

• K11=(−1)1+1M11=1×6=6$K_{11}={\left(-1\right)}^{1+1}{M}_{11}=1\times 6=6$
• K12=(−1)1+2M12=−1×14=−14$K_{12}={\left(-1\right)}^{1+2}{M}_{12}=-1\times 14=-14$
• K13=(−1)1+3M13=1×10=10$K_{13}={\left(-1\right)}^{1+3}{M}_{13}=1\times 10=10$
• K21=(−1)2+1M21=−1×(−14)=14$K_{21}={\left(-1\right)}^{2+1}{M}_{21}=-1\times \left(-14\right)=14$
• K22=(−1)2+2M11=1×10=10$K_{22}={\left(-1\right)}^{2+2}{M}_{11}=1\times 10=10$
• K23=(−1)2+3M11=−1×(−2)=2$K_{23}={\left(-1\right)}^{2+3}{M}_{11}=-1\times \left(-2\right)=2$
• K31=(−1)3+1M31=1×2=2$K_{31}={\left(-1\right)}^{3+1}{M}_{31}=1\times 2=2$
• K32=(−1)3+2M32=−1×(−6)=6$K_{32}={\left(-1\right)}^{3+2}{M}_{32}=-1\times \left(-6\right)=6$
• K33=(−1)3+3M33=1×14=14$K_{33}={\left(-1\right)}^{3+3}{M}_{33}=1\times 14=14$

Berdasarkan uraian di atas, dapat kita simpulkan bahwa kofaktor dari matriks A adalah K=⎛⎝⎜⎜6142−1410610214 ⎞⎠⎟⎟$K=\left(\begin{array}{ccc}6& -14& 10\\ 14& 10& 2\\ 2& 6& 14\end{array}\right)$.

Rumus Cepat

Jika kalian cermati nilai dari (−1)i+j$(-1{)}^{i+j}$, maka kalian akan memperoleh matriks kofaktor sebagai berikut: K=⎛⎝⎜⎜M11−M21M31−M12M22−M32M13−M23M33 ⎞⎠⎟⎟$K=\left(\begin{array}{ccc}{M}_{11}& -M_{12}& M_{13}\\ -M_{21}& M_{22}& -M_{23}\\ M_{31}& -M_{32}& M_{33}\end{array}\right)$.

Pada matriks di atas, terlihat bahwa elemen matriks kofaktor sama dengan elemen matriks minor, hanya saja ada perubahan tanda pada beberapa elemennya.

Jika kalian perhatikan lagi, tanda negatif pada setiap elemennya berselang-seling, dimulai dari baris pertama.

Nah, kalian sudah selesai mempelajari topik ini. Cobalah mengerjakan latihan soal dalam topik ini untuk menguji pemahaman kalian.

Share this post