Hubungan Matriks, Determinan Matriks, dan Invers Matriks
Hubungan Matriks, Determinan Matriks, dan Invers Matriks - Pada topik sebelumnya kalian telah belajar tentang bagaimana menghitung determinan matriks berordo 1 x 1 maupun 2 x 2. Selain itu kalian juga telah belajar tentang bagaimana menentukan invers suatu matriks berordo 2 x 2 maupun 3 x 3.
Contoh 1:
Nah, bagaimanakah cara menentukan determinan suatu matriks berordo 3 x 3?
Contoh 2:
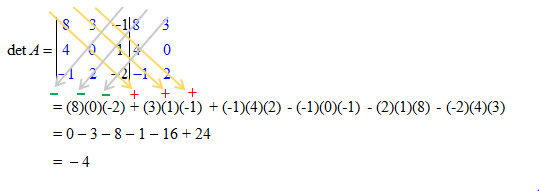
Invers Matriks Berordo 2 x 2
Contoh 3:
Invers Matriks Berordo 3 x 3
Contoh 4:
Nah, sekarang mari kita analisa hubungan antara determinan matriks B dengan determinan invers matriksnya.
Apa yang dapat kalian simpulkan dari contoh 4 di atas?
Nah, apa hubungan antara determinan matriks AA-1 dan -1A?
Ayo uji pemahaman kalian dengan mengerjakan sepuluh latihan soal dalam topik ini.
 |
| Hubungan Matriks, Determinan Matriks, dan Invers Matriks |
Apakah diantara kalian ada yang telah lupa?
Baiklah kita ulangi secara singkat materi tentang determinan dan invers suatu matriks untuk memudahkan kalian dalam mempelajari materi ini.
Determinan Matriks
Apabila diberikan matriks berordo 2 x 2: , maka determinan dari matriks A tersebut adalah .
Contoh 1:
Tentukan determinan matriks .
Penyelesaian:
Pada soal di atas, a = 2, b = 3, c = 4, dan d = 1.
Dengan demikian,
Nah, bagaimanakah cara menentukan determinan suatu matriks berordo 3 x 3?
Ya, determinan suatu matriks berordo 3 x 3 dapat ditentukan dengan menggunakan konsep kofaktor maupun kaidah Sarrus.
Contoh 2:
Diketahui matriks . Tentukan determinan matriks A dengan menggunakan kaidah Sarrus.
Penyelesaian:
Menentukan determinan matriks A dengan menggunakan kaidah Sarrus adalah sebagai berikut:
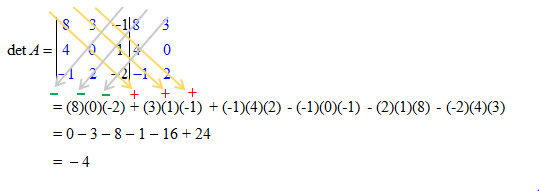
Berdasarkan uraian di atas, dapat disimpulkan bahwa determinan matriks A adalah –4.
Invers Matriks
Misal diberikan matriks persegi A dan B. Matriks A dan B dikatakan saling invers apabila AB = I, dengan I adalah matriks identitas.
Nah, tahukan kalian bagaimana cara menentukan invers dari suatu matriks?
Ya, invers suatu matriks dapat ditentukan dengan menggunakan metode Gauss-Jordan atau dengan menggunakan rumus: , dengan adj(A) adalah adjoint dari matriks A.
Invers Matriks Berordo 2 x 2
Jika matriks , maka .
Contoh 3:
Tentukan invers dari matriks .
Penyelesaian:
Berdasarkan rumus invers matriks, kita peroleh hasil sebagai berikut:
Invers Matriks Berordo 3 x 3
Dalam menentukan invers matriks A berordo 3 x 3, kalian juga dapat menggunakan rumus: . Nah, untuk menentukan nilai determinan matriks A, kalian dapat menggunakan kofaktor maupun kaidah Sarrus.
Hubungan Matriks, Determinan Matriks, dan Invers Matriks
Mari kita cari tahu hubungan antara matriks, determinan matriks, dan invers matriks melalui contoh berikut.
Contoh 4:
Diketahui dan .
Tentukan hubungan antara determinan matriks A dan B dengan determinan invers matriksnya.
Tentukan hubungan antara determinan matriks A dan B dengan determinan invers matriksnya.
Penyelesaian:
Sebelum menentukan hubungan antara determinan matriks A dengan determinan invers matriksnya, kita perlu menentukan terlebih dahulu nilai dari determinan matriks A, invers matriks A, dan determinan invers matriks A.
Berdasarkan uraian di atas, .
Nah, sekarang mari kita analisa hubungan antara determinan matriks B dengan determinan invers matriksnya.
Berdasarkan uraian di atas, ternyata .
Apa yang dapat kalian simpulkan dari contoh 4 di atas?
Ya, tentu saja bahwa determinan sebuah matriks tak nol akan sama dengan determinan invers matriksnya. Dengan kata lain, jika det (A) ≠ 0, maka .
Nah, apa hubungan antara determinan matriks AA-1 dan -1A?
Mari kita temukan jawabannya dengan mencermati uraian di bawah ini.
Telah kalian ketahui bahwa det (AB) = det (A) x det (B) dan AA-1 = A-1A = I, dengan Iadalah matriks identitas.
Dengan demikian,
Ayo uji pemahaman kalian dengan mengerjakan sepuluh latihan soal dalam topik ini.