Membuat Model Fungsi dari Masalah Nyata

Membuat Model Fungsi dari Masalah Nyata - Pada topik sebelumnya, kalian telah belajar mengenai teorema fundamental kalkulus 1 dan 2. Nah, dalam topik ini kalian akan belajar tentang bagaimana memodelkan permasalahan nyata ke dalam bentuk integral tentu.

Membuat Model Fungsi dari Masalah Nyata

Perlu kalian ketahui, permasalahan nyata yang dapat dimodelkan ke dalam bentuk integral akan banyak kalian jumpai dari bidang ekonomi, fisika, biologi, dan kimia.

Apakah kalian masih ingat tentang definisi integral?

Ya, integral merupakan anti turunan, sedangkan turunan menyatakan besarnya perubahan suatu besaran akibat perubahan besaran lainnya.

Sebagai contoh, misalkan benda A$A$ bergerak dari titik O$O$ menuju titik P$P$. Nah, perubahan jarak antara titik O$O$ dan benda A$A$ setiap satuan waktu disebut kecepatan. Adapun integral dari kecepatan dalam kasus ini adalah jarak antara titik O$O$ dan P$P$.

Contoh lain yang menggambarkan hubungan antara turunan dan integral adalah sebagai berikut:

• Besarnya volume air yang mengalir dari suatu kran setiap satuan waktu disebut debit air. Dalam kasus ini, integral dari fungsi debit air adalah fungsi volume air.
• Kenaikan biaya yang harus dibayarkan sebuah pabrik karena memproduksi satu barang tambahan disebut biaya marginal. Dalam kasus ini, integral dari fungsi biaya marginal disebut fungsi biaya total.
• Perubahan banyaknya senyawa yang dihasilkan dari suatu reaksi setiap satuan waktu disebut laju reaksi. Nah, banyak senyawa yang dihasilkan pada satuan waktu tertentu dapat dihitung dengan cara mengintegralkan fungsi laju reaksi.

Agar kalian lebih paham tentang bagaimana cara memodelkan masalah nyata ke dalam bentuk integral tentu, yuk kita cermati beberapa soal berikut.

Contoh 1

Kecepatan suatu mobil balap (m/s) selalu berubah-ubah, sesuai dengan fungsi v(t)=30t−20$v(t)=30t-20$. Bagaimanakah bentuk integral yang digunakan untuk menentukan jarak tempuh mobil balap pada detik ke-3 hingga detik ke-10?

Penyelesaian:

Seperti yang telah kalian ketahui, fungsi jarak merupakan integral dari fungsi kecepatan.

Dengan demikian, jarak yang ditempuh mobil balap pada detik ke-3 hingga detik ke-10 dapat ditulis dalam notasi integral: ∫310(30t−20)dt$\underset{3}{\overset{10}{\int }}\left(30t-20\right)dt$.

Jika batas integral dari masalah nyata yang diberikan tidak diketahui, maka bagaimanakah cara memodelkannya?

Yuk kita cari tahu jawabannya dengan memperhatikan contoh berikut.

Contoh 2

Kecepatan sebuah sepeda (m/s) berubah-ubah sesuai fungsi v(t)=5t−1$v(t)=5t-1$. Ketika kecepatan sepeda adalah 14 m/s, stopwatch dinyalakan, dan ketika kecepatan sepeda adalah 29 m/s, stopwatch dimatikan. Bagaimanakah bentuk integral yang digunakan untuk menentukan jarak yang telah ditempuh sepeda selama stopwatch dinyalakan hingga dimatikan?

Penyelesaian:

Misalkan stopwatch dinyalakan pada detik ke-a$a$ dan dimatikan pada detik ke-b$b$.

Dengan demikian,

• v(a)=14⇔5t−1=14⇔5t=15⇔t=3$v\left(a\right)=14\iff 5t-1=14\iff 5t=15\iff t=3$
• (v(b)=29⇔5t−1=29⇔5t=30⇔t=6$(v\left(b\right)=29\iff 5t-1=29\iff 5t=30\iff t=6$

Berdasarkan uraian di atas, dapat disimpulkan bahwa stopwatch dinyalakan pada detik ke-3 dan dimatikan pada detik ke-6.

Jadi, jarak yang telah ditempuh sepeda selama stopwatch dinyalakan hingga dimatikan dapat ditulis dengan notasi: ∫36(5t−1)dt$\underset{3}{\overset{6}{\int }}\left(5t-1\right)dt$.

Perlu kalian ketahui, terkadang dalam masalah nyata yang diberikan, fungsi yang akan diintegralkan belum diketahui.

Tahukah kalian bagaimana cara menentukan bentuk integralnya?

Yuk kita temukan jawabannya dengan mencermati contoh 3 berikut ini.

Contoh 3

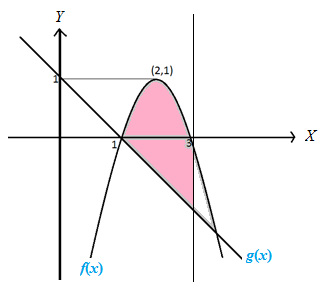
Seorang arsitek hendak membuat terowongan di suatu daerah dengan lahan miring dan berbukit. Ilustrasi dari bagian depan bentuk terowongan tersebut adalah sebagai berikut:

Berapakah luas bagian berwarna pink?

Penyelesaian:

Perhatikan bahwa persamaan garis dan parabola pada ilustrasi di atas belum diketahui.

Oleh karena garis lurus pada ilustrasi di atas melalui titik (0,1)$(0,1)$ dan (1,0)$(1,0)$, maka persamaan garis tersebut adalah x+y=1⇔y=1−x$x+y=1\iff y=1-x$.

Oleh karena titik yang dilalui oleh parabola pada ilustrasi di atas adalah titik (1,0)$(1,0)$, (3,0)$(3,0)$, dan (2,1)$(2,1)$, maka

• f(x)=a(x−1)(x−3)$f\left(x\right)=a\left(x-1\right)\left(x-3\right)$
• f(2)=1$f\left(2\right)=1$

Dengan demikian,

f(2)=1⇔a(2−1)(2−3)=1⇔a(1)(−1)=1⇔−a=1⇔a=−1$\begin{array}{l}f\left(2\right)=1\\ \iff a\left(2-1\right)\left(2-3\right)=1\\ \iff a\left(1\right)\left(-1\right)=1\\ \iff -a=1\\ \iff a=-1\end{array}$

Jadi, f(x)=−1(x−1)(x−3)=−x2+4x−3$f\left(x\right)=-1\left(x-1\right)\left(x-3\right)=-x^2+4x-3$.

Nah, karena pada interval [1,3]$[1,3]$ letak parabola f(x)=−x2+4x−3$f(x)=-x^2+4x-3$ adalah di atas garis g(x)=1−x$g(x)=1-x$, maka bentuk integral untuk menentukan luas daerah berwarna pink adalah sebagai berikut:

L===∫13(f(x)−g(x))dx∫13(−x2+4x−3−(1−x))dx∫13(−x2+5x−4)dx

Share this post