Pemecahan Masalah Nyata dengan Menggunakan Integral Tentu

Pemecahan Masalah Nyata dengan Menggunakan Integral Tentu - Pada topik-topik sebelumnya kalian telah belajar mengenai konsep dasar integral tentu. Nah, dalam topik ini kalian akan belajar tentang bagaimana menggunakan konsep integral tentu dalam menyelesaikan masalah nyata.

Pemecahan Masalah Nyata dengan Menggunakan Integral Tentu

Ada banyak masalah nyata yang dapat kalian hubungkan dengan konsep integral tentu, seperti masalah dalam bidang ekonomi, fisika, dan pembangunan.

Dalam bidang ekonomi, konsep integral tentu biasanya digunakan untuk menentukan biaya rata-rata, nilai surplus konsumen, dan pendapatan distribusi. Adapun dalam bidang fisika, konsep integral tentu banyak digunakan untuk menentukan kecepatan, percepatan, dan usaha.

Coba tebak, dalam bidang pembangunan, masalah nyata apa saja yang dapat diselesaikan dengan menggunakan konsep integral tentu?

Tepat sekali. Luas dan volume suatu gedung yang hendak dibangun dapat ditentukan dengan menggunakan konsep integral tentu.

Agar kalian lebih mudah memahami materi ini, yuk kita perhatikan tiga contoh berikut.

Contoh 1: Biaya Rata-Rata

Biaya untuk memproduksi x$x$ unit charger dalam ribuan rupiah dinyatakan dalam fungsiC(x)=200+2x+0,3x2$C(x)=200+2x+0,3x^2$.

1. Tentukan biaya rata-rata C(x)$C(x)$ untuk memproduksi 10 sampai 20 unit charger.
2. Tentukan biaya rata-rata per unit jika 40 unit charger diproduksi.

Penyelesaian:

Dalam bidang ekonomi, nilai rata-rata dari suatu fungsi kontinu y=f(x)$y=f(x)$ pada interval [a,b]$[a,b]$ adalah NR=1b−a∫abf(x)dx$NR=\frac{1}{b-a}\underset{a}{\overset{b}{\int }}f(x)dx$.

Nah, berdasarkan rumus di atas, maka biaya rata-rata C(x)$C(x)$ untuk memproduksi 10 sampai 20 unit charger dapat ditentukan dengan cara sebagai berikut:

NR======1b−a∫abf(x)dx120−10∫1020(200+2x+0,3x2)dx110[200x+x2+0,1x3]2010110[(4.000+400+800)−(2.000+100+100)]110×3.000300$\begin{array}{lll}NR& =& \frac{1}{b-a}\underset{a}{\overset{b}{\int }}f(x)dx\\ & =& \frac{1}{20-}\end{array}$

$\begin{array}{l}\frac{10}{}\underset{10}{\overset{20}{\int }}\left(200+2x+0,3x^2\right)dx\\ & =& \frac{1}{10}{\left[200x+x^2+0,1x^3\right]}_{10}^{20}\\ & =& \frac{1}{10}[\left(4.000+400+800\right)-\end{array}$

$\begin{array}{l}\left(2.000+100+100\right)]\\ & =& \frac{1}{10}\times 3.000\\ & =& 300\end{array}$

Jadi, biaya rata-rata C(x)$C(x)$ untuk memproduksi 10 sampai 20 unit charger adalah Rp300.000,00.

Nah, karena C(x)$C(x)$ adalah biaya untuk memproduksi x$x$ unit charger, maka biaya rata-rata untuk memproduksi satu buah unit charger adalah C(x)⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯=C(x)x=200+2x+0,3x2x=200x+2+0,3x$\overline{C\left(x\right)}=\frac{C\left(x\right)}{x}=\frac{200+2x+0,3x^2}{x}=\frac{200}{x}+2+0,3x$.

Berdasarkan rumus di atas, biaya rata-rata per unit jika 40 unit charger diproduksi dapat ditentukan dengan cara sebagai berikut:

C(40)⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯===20040+2+0,3×405+2+1219$\begin{array}{lll}\overline{C\left(40\right)}& =& \frac{200}{40}+2+0,3\times 40\\ & =& 5+2+12\\ & =& 19\end{array}$

Jadi, biaya rata-rata per unit jika 40 unit charger diproduksi adalah Rp19.000,00.

Contoh 2: Surplus Konsumen

Fungsi permintaan suatu produk adalah p=49−6x‾‾‾‾‾‾‾√$p=\sqrt{49-6x}$ dan fungsi penawarannya adalah p=x+1$p=x+1$, dengan p$p$ adalah harga sebuah produk dalam ribu rupiah dan x$x$adalah banyaknya produk. Tentukan titik keseimbangan dan perkiraan nilai surplus konsumen.

Penyelesaian:

Titik keseimbangan diperoleh saat fungsi permintaan dan fungsi penawaran berpotongan.

x+1=49−6x‾‾‾‾‾‾‾√⇔(x+1)2=49−6x⇔x2+2x+1=49−6x⇔x2+8x−48=0⇔(x−4)(x+12)=0⇔x=4∨x=−12$\begin{array}{l}x+1=\sqrt{49-6x}\\ \iff {\left(x+1\right)}^2=49-6x\\ \iff x^2+2x+1=49-6x\\ \iff x^2+8x-48\end{array}$

$\begin{array}{l}=0\\ \iff \left(x-4\right)\left(x+12\right)=0\\ \iff x=4\vee x=-12\end{array}$

Oleh karena banyak produk tidak mungkin negatif, maka x=4$x=4$. Akibatnya, p=4+1=5$p=4+1=5$.

Jadi, titik keseimbangannya adalah (4,5)$(4,5)$.

Suplus konsumen adalah selisih antara besar uang yang disediakan konsumen untuk membeli suatu produk dengan harga produk yang sebenarnya.

Jika x1$x_1$ dan y1$y_1$ berturut-turut adalah absis dan ordinat dari titik keseimbangan, maka surplus konsumen dapat ditentukan dengan rumus berikut: SK=∫0x1f(x)dx−y1$SK=\underset{0}{\overset{x_1}{\int }}f\left(x\right)dx-y_1$.

SK========≈∫0x1f(x)dx−y1∫0449−6x‾‾‾‾‾‾‾√dx−5−16[23(49−6x)49−6x‾‾‾‾‾‾‾√]40−5−19[(49−24)49−24‾‾‾‾‾‾‾√−((49−0)49−0‾‾‾‾‾‾√)]−5−19(25×5−49×7)−5−19(125−343)−52189−5173919,22$\begin{array}{lll}SK& =& \underset{0}{\overset{x_1}{\int }}f\left(x\right)dx-y_1\end{array}$

$\begin{array}{lll}& =& \underset{0}{\overset{4}{\int }}\sqrt{49-6x}dx-5\\ & =& -\frac{1}{6}{\left[\frac{2}{3}\left(49-6x\right)\sqrt{49-6x}\right]}_0^4-5\\ & =& -\frac{1}{9}\left[\left(49-24\right)\sqrt{49-24}-\left(\left(49-0\right)\sqrt{49-0}\right)\right]-5\end{array}$

$\begin{array}{lll}& =& -\frac{1}{9}\left(25\times 5-49\times 7\right)-5\\ & =& -\frac{1}{9}\left(125-343\right)-5\\ & =& \frac{218}{9}-5\\ & =& \frac{173}{9}\\ & \approx & 19,22\end{array}$

Dengan demikian, perkiraan nilai surplus konsumen adalah Rp19.220,00.

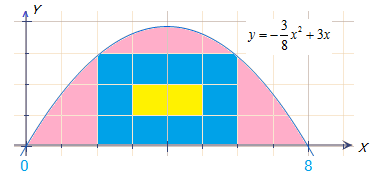
Contoh 3: Luas Daerah

Bagian atas pintu sebuah rumah berbentuk parabola, dengan persamaan y=−38x2+3x$y=-\frac{3}{8}{x}^2+3x$. Jika lebar pintu tersebut adalah 8 dm dan bagian atas pintu tersebut hendak diganti dengan kaca berwarna seharga Rp600.000,00 per meter persegi, maka berapakah biaya yang harus dikeluarkan oleh pemilik rumah?

Penyelesaian:

Permasalahan dalam soal dapat diilustrasikan sebagai berikut:

Berdasarkan ilustrasi di atas, daerah yang terbentuk dibatasi oleh parabola dan sumbuX$X$, serta berada pada interval [0,8]$[0,8]$.

Dengan demikian, luas daerah tersebut dapat ditentukan sebagai berikut:

L=====∫08(−38x2+3x)dx[−18x3+32x2]80−18(83)+32(82)−64+9632$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}L& =& \underset{0}{\overset{8}{\int }}\left(-\frac{3}{8}{x}^2+3x\right)dx\\ & =& {\left[-\frac{1}{8}{x}^3+\frac{3}{2}{x}^2\right]}_0^8\\ & =& -\frac{1}{8}\left(8^3\right)+\frac{3}{2}\left(8^2\right)\\ & =& -64+96\\ & =& 32\end{array}$

Nah, karena luas daerah adalah 32 dm2 = 0,32 m2, maka biaya yang perlu dikeluarkan oleh pemilik untuk mengganti bagian atas pintu dengan kaca berwarna adalah 0,32×Rp600.000,00=Rp192.000,00$0,32\times Rp600.000,00=Rp192.000,00$.

Kalian tentu sudah paham dengan penjelasan dalam ketiga contoh di atas bukan?

Share this post