Menghitung Luas daerah yang Dibatasi Kurva
Menghitung Luas daerah yang Dibatasi Kurva - Apakah kalian masih ingat dengan konsep jumlah Riemann yang telah kalian pelajari pada topik sebelumnya?
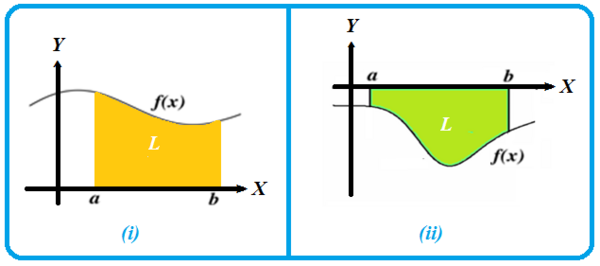
Oleh karena daerah pada gambar (i) berada di atas sumbu , maka luas daerah tersebut adalah .
Tahukah kalian bagaimana cara menghitung luas daerah dari gambar (ii) di atas?
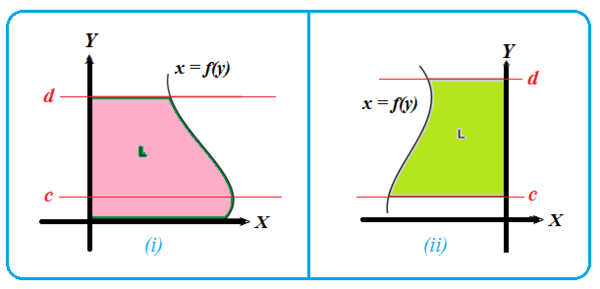
Oleh karena daerah pada gambar (i) berada di kanan sumbu , maka luas daerah tersebut adalah .
Tahukah kalian bagaimana cara menghitung luas daerah dari gambar (ii) di atas?
Perlu kalian ketahui, suatu daerah dapat juga dibatasi oleh dua kurva.
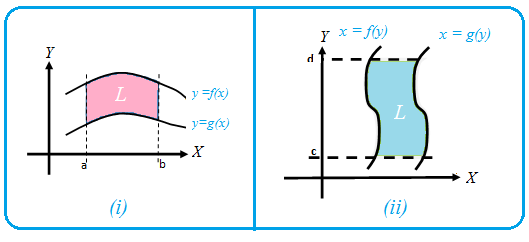
Jika sebuah daerah dibatasi oleh dua kurva seperti terlihat dalam gambar (i), maka luas daerah tersebut dapat ditentukan menggunakan rumus: .
Nah, jika suatu daerah dibatasi oleh dua kurva pada bagian sisi kanan dan kiri, seperti terlihat dalam gambar (ii), maka luas daerah tersebut dapat ditentukan menggunakan rumus: .
Apakah kalian sudah paham dengan materi di atas?
Penyelesaian:
Pada gambar (1), daerah berwarna biru berada di bawah sumbu , dibatasi oleh kurva , dan terletak pada interval .
Pada gambar (2), tampak ada dua daerah, yaitu daerah yang berada di bawah sumbu dan daerah yang berada di atas sumbu .
Pada gambar (3). daerah berwarna biru dibatasi oleh kurva dan garis , dimana letak kurva berada di atas garis.
 |
| Menghitung Luas daerah yang Dibatasi Kurva |
Yuk kita ingat kembali.

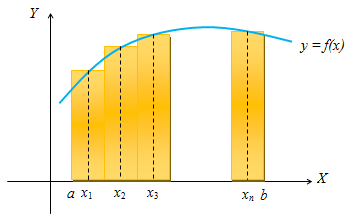
Berdasarkan konsep jumlah Riemann, jika fungsi kontinu dalam interval , maka luas daerah yang dibatasi oleh kurva , sumbu , garis , dan garis adalah .
Luas Daerah yang Dibatasi oleh Kurva y=f(x) dan sumbu X
Jika sumbu merupakan batas suatu daerah, maka daerah yang terbentuk dapat berada di atas sumbu atau di bawah sumbu .

Oleh karena daerah pada gambar (i) berada di atas sumbu , maka luas daerah tersebut adalah .
Tahukah kalian bagaimana cara menghitung luas daerah dari gambar (ii) di atas?
Jika kalian perhatikan, nilai fungsi pada daerah berwarna hijau pada gambar (ii) semuanya bernilai negatif. Nah, oleh karena luas suatu daerah selalu bernilai positif, maka bentuk integral haruslah bertanda negatif.
Dengan kata lain, luas daerah pada gambar (ii) adalah .
Luas Daerah yang Dibatasi oleh Kurva x=f(y) dan sumbu Y
Jika sumbu merupakan batas suatu daerah, maka daerah yang terbentuk dapat berada di kanan sumbu atau di kiri sumbu .

Oleh karena daerah pada gambar (i) berada di kanan sumbu , maka luas daerah tersebut adalah .
Tahukah kalian bagaimana cara menghitung luas daerah dari gambar (ii) di atas?
Jika kalian perhatikan, nilai absis pada daerah berwarna hijau pada gambar (ii) semuanya bernilai negatif. Nah, oleh karena luas suatu daerah selalu bernilai positif, maka bentuk integral haruslah bertanda negatif.
Dengan kata lain, luas daerah pada gambar (ii) adalah .
Perlu kalian ketahui, suatu daerah dapat juga dibatasi oleh dua kurva.
Lalu bagaimana cara menghitung luas daerah yang terbentuk?
Yuk temukan jawabannya dengan mencermati uraian berikut.
Luas Daerah yang Dibatasi oleh Dua Kurva

Jika sebuah daerah dibatasi oleh dua kurva seperti terlihat dalam gambar (i), maka luas daerah tersebut dapat ditentukan menggunakan rumus: .
Secara geografis, kalian diminta untuk mengurangkan persamaan kurva yang terletak di atas dengan persamaan kurva yang terletak di bawahnya.
Nah, jika suatu daerah dibatasi oleh dua kurva pada bagian sisi kanan dan kiri, seperti terlihat dalam gambar (ii), maka luas daerah tersebut dapat ditentukan menggunakan rumus: .
Nah, dalam kasus ini, kalian diminta untuk mengurangkan persamaan kurva yang terletak di sebelah kanan dengan persamaan kurva yang terletak di sebelah kiri.
Apakah kalian sudah paham dengan materi di atas?
Yuk kita cermati beberapa contoh berikut agar kalian semakin paham.
Contoh
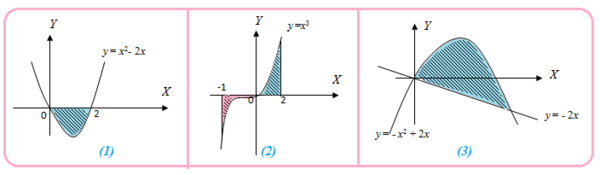
Tentukan luas daerah daerah dari gambar berikut.

Penyelesaian:
Pada gambar (1), daerah berwarna biru berada di bawah sumbu , dibatasi oleh kurva , dan terletak pada interval .
Dengan demikian, luas daerah berwarna biru tersebut adalah
satuan luas.
Pada gambar (2), tampak ada dua daerah, yaitu daerah yang berada di bawah sumbu dan daerah yang berada di atas sumbu .
Dengan demikian, luas kedua daerah tersebut dapat ditentukan dengan cara sebagai berikut:
Berdasarkan uraian di atas, luas daerah pada gambar (2) adalah satuan luas.
Pada gambar (3). daerah berwarna biru dibatasi oleh kurva dan garis , dimana letak kurva berada di atas garis.
Nah, untuk menentukan luas daerah berwarna biru, kita perlu menentukan terlebih dahulu absis titik potong antara kurva dan garis.
Berdasarkan uraian di atas, maka luas daerah berwarna biru dapat ditentukan dengan cara sebagai berikut: