Konsep Jumlah Riemann
Konsep Jumlah Riemann - Pada waktu kalian SMP, kalian telah belajar bagaimana menghitung luas daerah bidang datar, seperti luas persegi, persegipanjang, belah ketupat, layang-layang, dan jajar genjang.
Nah, tahukah kalian bagaimana cara menghitung luas daerah bidang datar jika bidangnya tidak beraturan?
Yuk kita pelajari lebih lanjut konsep tersebut.
Misalkan diketahui fungsi kontinu dalam interval . Nah, kita akan mencoba menghitung luas daerah yang dibatasi oleh kurva , sumbu , garis, dan garis .
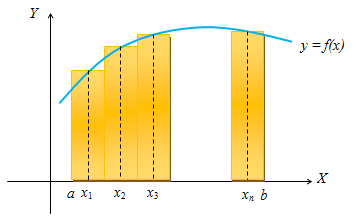
Pada sketsa di atas, tampak bahwa ada persegipanjang dengan lebar sama, misalkan .
Perlu kalian ketahui, bentuk inilah yang disebut sebagai jumlah Riemann.
Selanjutnya, untuk menentukan luas daerah , kita perlu mengambil nilai yang cukup besar.
Bentuk selanjutnya disebut dengan integral tentu atau integral Riemann.
Apakah kalian sekarang sudah paham dengan definisi dari jumlah Riemann dan integral Riemann?
Penyelesaian:
Berdasarkan informasi dalam soal, dapat kita buat sketsa sebagai berikut:
Penyelesaian:
Permasalahan dalam soal dapat diilustrasikan sebagai berikut:

Perlu kalian ketahui, jumlah Rieman di atas akan mendekati luas daerah yang sebenarnya jika nilai .
 |
| Konsep Jumlah Riemann |
Nah, tahukah kalian bagaimana cara menghitung luas daerah bidang datar jika bidangnya tidak beraturan?
Ya, untuk menghitung luas daerah bidang datar tak beraturan, kalian perlu menggunakan konsep jumlah Riemann.
Yuk kita pelajari lebih lanjut konsep tersebut.
Konsep Jumlah Riemann
Untuk memudahkan kalian dalam memahami konsep jumlah Riemann, mari kita perhatikan ilustrasi berikut.
Misalkan diketahui fungsi kontinu dalam interval . Nah, kita akan mencoba menghitung luas daerah yang dibatasi oleh kurva , sumbu , garis, dan garis .

Pada sketsa di atas, tampak bahwa ada persegipanjang dengan lebar sama, misalkan .
Sebagai pendekatan untuk menentukan luas daerah , kita tentukan terlebih dahulu jumlah luas dari buah persegipanjang dalam sketsa.
Persamaan di atas juga dapat dinyatakan dalam notasi sigma: .
Selanjutnya, karena ujung-ujung interval adalah dan , maka notasi sigma di atas dapat ditulis menjadi .
Perlu kalian ketahui, bentuk inilah yang disebut sebagai jumlah Riemann.
Selanjutnya, untuk menentukan luas daerah , kita perlu mengambil nilai yang cukup besar.
Nah, karena , maka menjadi semakin kecil .
Dengan demikian, luas daerah dapat ditentukan dengan rumus pendekatan berikut: .
Bentuk selanjutnya disebut dengan integral tentu atau integral Riemann.
Apakah kalian sekarang sudah paham dengan definisi dari jumlah Riemann dan integral Riemann?
Yuk kita cermati beberapa contoh berikut agar kalian semakin paham.
Contoh 1
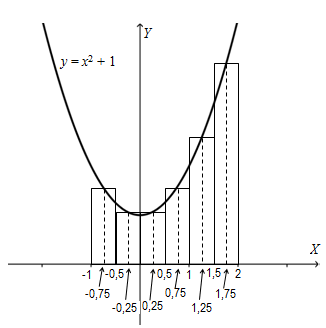
Hitunglah jumlah Riemann untuk fungsi pada interval , dimana interval tersebut terbagi menjadi enam bagian yang sama panjang dan titik merupakan titik tengah dari bagian ke-.
Penyelesaian:
Berdasarkan informasi dalam soal, dapat kita buat sketsa sebagai berikut:

Oleh karena interval dibagi menjadi enam bagian yang sama panjang, maka panjang setiap bagian adalah satuan.
Selanjutnya karena merupakan titik tengah dari bagian ke-, maka
- →
- →
- →
- →
- →
- →
Dengan demikian, jumlah Riemann dari fungsi dalam soal adalah sebagai berikut:
Contoh 2
Dengan menggunakan jumlah Riemann, hitunglah luas daerah yang dibatasi oleh garis dan sumbu , serta terletak pada interval .
Penyelesaian:
Permasalahan dalam soal dapat diilustrasikan sebagai berikut:

Jika interval kita bagi menjadi interval yang sama panjang, maka panjang masing-masing interval adalah .
Selanjutnya jika merupakan titik tengah dari bagian ke-, maka
☟
Berdasarkan uraian di atas, dapat disimpulkan bahwa .
Akibatnya,
Dengan demikian, jumlah Riemann dari fungsi adalah sebagai berikut:
Perlu kalian ketahui, jumlah Rieman di atas akan mendekati luas daerah yang sebenarnya jika nilai .