Penerapan Diagonal Ruang, Diagonal Bidang, dan Bidang Diagonal dalam Kehidupan Sehari-Hari

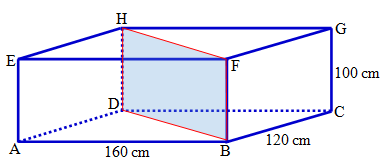
Penerapan Diagonal Ruang, Diagonal Bidang, dan Bidang Diagonal dalam Kehidupan Sehari-Hari - Tono hendak membuat kandang berukuran 160 cm × 120 cm × 100 cm untuk ayam peliharaannya. Kandang tersebut selanjutnya akan ia bagi menjadi dua bagian sedemikian hingga terbentuk dua prisma segitiga dengan volume dan luas sama. Selanjutnya sebagai pembatas ruang, Tono menggunakan kayu triplek.

Penerapan Diagonal Ruang, Diagonal Bidang, dan Bidang Diagonal dalam Kehidupan Sehari-Hari

Dapatkah kalian menentukan luas kayu triplek yang dijadikan pembatas ruangan?

Ya, kalian tentu dapat menentukan luas kayu triplek tersebut. Nah, caranya adalah dengan menggunakan konsep diagonal ruang, diagonal bidang, dan bidang diagonal.

Sebelum kita menyelesaikan permasalahan dalam ilustrasi di atas, yuk kita cermati dua contoh berikut.

Contoh 1: Penerapan Diagonal Bidang

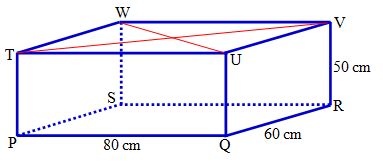
Dedi mempunyai akuarium berbentuk balok dengan panjang 80 cm, lebar 60 cm, dan tinggi 50 cm. Pada akuarium tersebut akan ditambahkan hiasan yang digantungkan pada seutas kawat yang dipasang di atas akuarium secara melintang dari ujung-ujungnya. Berapakah panjang kawat yang diperlukan?

Penyelesaian:

Permasalahan dalam contoh soal di atas dapat diilustrasikan sebagai berikut:

Berdasarkan ilustrasi di atas, panjang kawat yang dibutuhkan merupakan penjumlahan dari panjang diagonal bidang WU$WU$ dan TV$TV$.

Selanjutnya, dengan menggunakan teorema Pythagoras, panjang diagonal WU$WU$ dapat ditentukan dengan cara berikut:

WU====WV2+VU2‾‾‾‾‾‾‾‾‾‾‾‾√802+602‾‾‾‾‾‾‾‾‾√10.000‾‾‾‾‾‾√100$\begin{array}{lll}WU& =& \sqrt{W{V}^2+V{U}^2}\\ & =& \sqrt{{80}^2+{60}^2}\\ & =& \sqrt{10.000}\\ & =& 100\end{array}$

Nah, karena panjang diagonal TV$TV$ sama dengan panjang diagonal WU$WU$, maka panjang kawat yang diperlukan adalah 2×100=200$2\times 100=200$ cm.

Contoh 2: Penerapan Diagonal Ruang

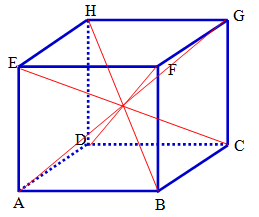
Adi berencana membuat kolam pemeliharaan lele yang berbentuk kubus dengan panjang sisi 2 m. Sebelum dilakukan pengecoran, Adi mempersiapkan kerangka yang terbuat dari besi. Agar kerangka yang dibuat tegak lurus, maka ia berencana mengikat bagian pojok kerangka yang saling berhadapan dengan menggunakan kawat yang kuat. Berapakah panjang kawat minimal yang diperlukan?

Penyelesaian:

Kerangka kolam lele dapat diilustrasikan sebagai berikut:

Pada ilustrasi di atas, tampak bahwa keempat kawat yang dibutuhkan merupakan diagonal ruang kubus ABCD.EFGH$ABCD.EFGH$, yaitu AG$AG$, BH$BH$, CE$CE$, dan DF$DF$, dimana panjangnya adalah 22‾√$2\sqrt{2}$ m.

Jadi, panjang kawat minimal yang dibutuhkan adalah 4×22‾√=82‾√$4\times 2\sqrt{2}=8\sqrt{2}$ m.

Apakah kalian sudah jelas dengan penjelasan di atas?

Yuk kita selesaikan permasalahan kandang ayam pada awal topik.

Contoh 3: Penerapan Bidang Diagonal

Berikut ini adalah ilustrasi dari kandang ayam yang hendak dibuat oleh Tono.

Pada ilustrasi di atas, tampak bahwa untuk menentukan luas triplek, kita perlu mengetahui panjang diagonal bidang BD$BD$ terlebih dahulu.

Oleh karena ∆BCD$∆BCD$ siku-siku di titik C$C$, maka panjang diagonal bidang BD$BD$ dapat ditentukan sebagai berikut:

BD====BC2+CD2‾‾‾‾‾‾‾‾‾‾‾√1202+1602‾‾‾‾‾‾‾‾‾‾‾‾√40.000‾‾‾‾‾‾√200$\begin{array}{lll}BD& =& \sqrt{B{C}^2+C{D}^2}\\ & =& \sqrt{{120}^2+{160}^2}\\ & =& \sqrt{40.000}\\ & =& 200\end{array}$

Dengan demikian, luas kayu triplek adalah BD×BF=200×100=20.000$BD\times BF=200\times 100=20.000$ cm2.

Share this post