Contoh Soal Pangkat Nol dan Negatif
Contoh Soal Pangkat Nol dan Negatif - Pada topik sebelumnya telah dibahas bahwa definisi dari an adalah perkalian berulang bilangan a sebanyak n kali.
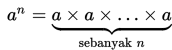
Yuk kita perhatikan beberapa contoh berikut.
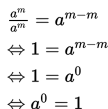
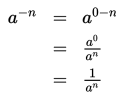
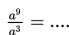
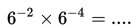
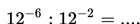
Jika a > 0, a ≠ 1, dan n merupakan bilangan bulat positif, maka
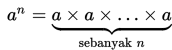
Nah, kali ini kita akan menambah pengetahuan kita tentang pembagian bilangan berpangkat.
Salah satu sifat pembagian bilangan berpangkat adalah .
Contoh 1: Tentukan nilai dari .
Penyelesaian:
Jika kita gunakan sifat pembagian bilangan berpangkat, maka .
Jika kita gunakan definisi bilangan berpangkat, maka .
Hasil yang diperoleh sama bukan?
Saat nilai dari bilangan berpangkat kecil, kedua cara di atas memang nampak sama-sama mudah dan cepat. Namun tidak demikian ketika nilai bilangan berpangkatnya besar.
Mengapa demikian?
Mari kita simak contoh berikut.
Mari kita simak contoh berikut.
Contoh 2: Tentukan nilai dari .
Penyelesaian:
Jika kita gunakan sifat pembagian bilangan berpangkat, maka .
Jika kita gunakan definisi bilangan berpangkat, maka .
Meskipun hasilnya sama, namun membagi bilangan berpangkat tanpa memanfaatkan sifat pembagian bilangan berpangkat akan cukup merepotkan ketika nilai bilangan berpangkatnya cukup besar.
Nah, sekarang kalian tahu sudah tahu kan, mana cara yang lebih mudah dan praktis untuk digunakan?
Selain sifat di atas, masih ada satu sifat lagi yang dapat mempermudah kalian dalam menentukan hasil pembagian bilangan berpangkat, yaitu: .
Yuk kita perhatikan beberapa contoh berikut.
Contoh 3: Tentukan nilai dari .
Penyelesaian:
Jika kita gunakan sifat pembagian bilangan berpangkat, maka .
Jika kita gunakan definisi bilangan berpangkat, maka .
Cukup mudah dimengerti bukan?
Mari kita perhatikan contoh selanjutnya.
Mari kita perhatikan contoh selanjutnya.
Contoh 4: Tentukan nilai dari .
Penyelesaian:
Akan merepotkan jika kita harus menghitung nilai dari 253 dan 1253 terlebih dahulu, kemudian menentukan hasil bagi keduanya, terlebih saat kita diharapkan untuk memperoleh hasil yang benar dalam waktu yang relatif singkat.
Nah, permasalahan di atas akan menjadi lebih mudah diselesaikan jika kita gunakan sifat pembagian bilangan berpangkat.
Jika kita gunakan sifat pembagian berpangkat, .
PANGKAT NOL
Pernahkah kalian melihat bentuk 20 , 30, 40 atau sejenisnya?
Menurut kalian, jika suatu bilangan dipangkatkan nol, berapakah hasilnya?
Menurut kalian, jika suatu bilangan dipangkatkan nol, berapakah hasilnya?
Jika kalian menjawab nol, maka jawaban kalian tersebut salah.
Ingin tahu mengapa?
Yuk kita simak penjelasan berikut.
Yuk kita simak penjelasan berikut.
Berdasarkan sifat pembagian bilangan berpangkat,
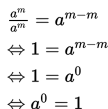
Sifat di atas berlaku untuk setiap bilangaan riil a dimana a ≠ 0.
Jadi, setiap bilangan bilangan riil yang bukan nol apabila dipangkatkan nol, maka hasilnya adalah satu.
Contoh:
- 20 = 1
- 50 = 1
- 1390 = 1
PANGKAT NEGATIF
Selain pangkat nol, suatu bilangan dapat pula dipangkatkan dengan bilangan negatif. Nah, untuk menentukan hasil dari pangkat negatif dari suatu bilangan, kita perlu menggunakan sifat pembagian bilangan berpangkat dan sifat pangkat nol dari bilangan berpangkat.
Perhatikan uraian berikut ini.
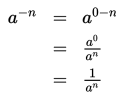
Sifat di atas berlaku untuk setiap bilangaan riil a dimana a ≠ 0.
S1
Pilihan Tunggal
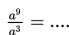
S2
Pilihan Tunggal
Jika k anggota himpunan bilangan riil dan k ≠ 0, maka k -2 = ….
S3
Pilihan Tunggal
Jika a ≠ 0 dan a merupakan bilangan riil, maka nilai n yang memenuhi an = 1 adalah ….
S4
Pilihan Tunggal
Nilai dari adalah ….
S5
Pilihan Tunggal
Nilai n yang memenuhi 9n = 1 adalah ….
S6
Pilihan Tunggal
Nilai dari 5-2 adalah ….
S7
Pilihan Tunggal
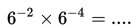
S8
Pilihan Tunggal
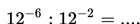
S9
Pilihan Tunggal
Nilai dari adalah ….
S10
Pilihan Tunggal
Nilai dari adalah ….
