Contoh Soal Syarat Kesebangunan Bangun Datar

Contoh Soal Syarat Kesebangunan Bangun Datar - Dua buah bangun dikatakan sebangun jika kedua bangun tersebut memiliki bentuk yang sama dengan ukuran yang bisa sama ataupun berbeda. Cara penulisan bangun-bangun yang sebangun yaitu dengan menggunakan simbol “~”, misalnya bangun PQRS sebangun dengan bangun KLMN, maka ditulis PQRS ~ KLMN. Sekarang, coba perhatikan sekelilingmu. Dapatkah kamu menyebutkan benda-benda yang sebangun? Ya, foto dengan pigura merupakan salah satu contohnya.

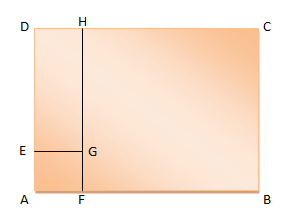
Perhatikan gambar persegi panjang berikut:

Apakah persegipanjang ABCD sebangun dengan persegipanjang KLMN?

       Persegipanjang ABCD dan KLMN sebangun karena mereka mempunyai bentuk yang sama, meskipun dengan ukuran yang berbeda. Berdasarkan pengamatan dari kedua bangun tersebut, diketahui bahwa:

• sudut-sudut yang bersesuaian sama besar, yaitu setiap sudut besarnya 90°
• sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai

Perbandingan sisi-sisi kedua persegipanjang tersebut dapat dituliskan sebagai berikut.

$\frac{AB}{KL}=\frac{4}{20}=\frac{1}{5}$

$\frac{BC}{LM}=\frac{3}{15}=\frac{1}{5}$

$\frac{DC}{NM}=\frac{4}{20}=\frac{1}{5}$

$\frac{DA}{NK}=\frac{3}{15}=\frac{1}{5}$

Dengan demikian, diperoleh hubungan antara sisi-sisi kedua bangun tersebut, yaitu:

$\frac{AB}{KL}=\frac{BC}{LM}=\frac{DC}{NM}=\frac{DA}{NK}$

Dari uraian di atas dapat diketahui bahwa dua bangun dikatakan sebangun, jika memenuhi syarat berikut:

Syarat Kesebangunan

• sudut-sudut yang bersesuaian sama besar
• sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai

       Oleh karena dua bangun dikatakan sebangun apabila sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai, maka kita dapat menghitung panjang salah satu sisi yang belum diketahui dengan menggunakan konsep perbandingan seperti pada contoh berikut ini.

Contoh

Contoh 1:

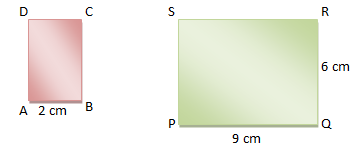
Apakah masing-masing pasangan bangun di bawah ini sebangun?

Penyelesaian:

Dua bangun dikatakan sebangun jika:

• sudut – sudut yang bersesuaian sama besar
• sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai

a. Oleh karena kedua bangun tersebut mempunyai bentuk yang sama, yaitu persegipanjang, maka sudut yang bersesuaian sama besar, yaitu 90°, dan sisi-sisi yang bersesuaian adalah:

$\frac{AB}{EF}=\frac{2}{4}=\frac{1}{2}$

$\frac{BC}{FG}=\frac{4}{8}=\frac{1}{2}$

Terlihat bahwa sisi-sisi yang bersesuaian sebanding.

Jadi, dapat disimpulkan bahwa ABCD dan EFGH adalah dua bangun yang sebangun.

b. Oleh karena kedua bangun tersebut mempunyai bentuk yang sama, yaitu trapesium, maka sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian adalah:

$\frac{PQ}{TU}=\frac{2}{1}$

$\frac{RQ}{VU}=\frac{5}{3}$

Oleh karena sisi-sisi yang bersesuaian tidak sebanding, maka bangun PQRS dan TUVW adalah dua bangun yang tidak sebangun.

Contoh 2:

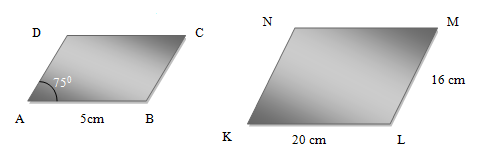
Perhatikan gambar berikut:

Trapesium ABCD dan PQRS sebangun, tentukanlah:

a. Panjang BC

b. Panjang RS

Penyelesaian:

Perbandingan sisi-sisi yang bersesuaian adalah:

$\frac{AB}{PQ}=\frac{6}{9}=\frac{2}{3}$

a. $\frac{BC}{QR}=\frac{AB}{PQ}$

$\iff \frac{BC}{12}=\frac{2}{3}$

$\iff BC=\frac{2}{3}\times 12=8\mathrm{c}\mathrm{m}$

Jadi, panjang BC adalah 8 cm.

b. $\frac{CD}{RS}=\frac{AB}{PQ}$

$\iff \frac{10}{RS}=\frac{2}{3}$

$\iff RS=\frac{3}{2}\times 10=15\mathrm{c}\mathrm{m}$

Jadi, panjang RS adalah 15 cm.

S1

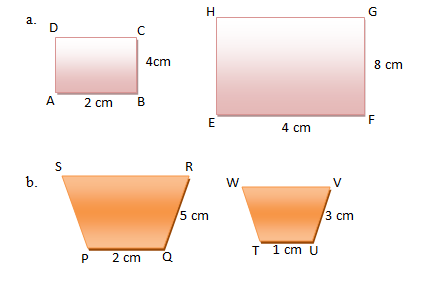
Bangun-bangun berikut pasti sebangun, kecuali .…

S2

Dua bangun persegipanjang di bawah ini adalah sebangun.

Pernyataan berikut ini yang benar adalah ....

S3

Diketahui beberapa lahan dengan bentuk dan ukuran berikut:

(i) Persegipanjang dengan ukuran 36 m × 27 m

(ii) Persegipanjang dengan ukuran 6 m x 4,5 m

(iii) Persegipanjang dengan ukuran 48 m × 24 m

(iv) Persegipanjang dengan ukuran 2,4 m × 1,8 m

Bangun di atas yang sebangun dengan selembar karton berbentuk persegipanjang dengan ukuran panjang 16 cm dan lebar 12 cm adalah ….

S4

Perhatikan gambar berikut.

Jika persegipanjang ABCD dan PQRS sebangun, maka panjang BC adalah … cm

S5

Perhatikan gambar di bawah ini.

Bangun ABCD dan PQRS sebangun. Diketahui AB = 8 cm, CD = 6 cm, AD = 12 cm, PQ = 4 cm, dan QR = 6 cm. Panjang SR adalah ….

S6

Perhatikan gambar berikut.

Jika jajargenjang ABCD dan KLMN sebangun, maka ∠KNM dan panjang BC berturut-turut adalah ....

S7

Sebuah persegipanjang A memiliki lebar 48 cm dan panjang 64 cm. Persegipanjang tersebut sebangun dengan persegipanjang B yang mempunyai panjang 18 cm. Lebar persegipanjang B adalah ....

S8

Sebuah persegipanjang memiliki ukuran seperti gambar di bawah ini.

Persegipanjang tersebut akan ditambahkan bingkai pada sisi kanan, kiri, dan atas selebar 6 cm, dan pada sisi bawah selebar x cm. Jika diketahui persegipanjang sebelum dan sesudah dibingkai (persegipanjang dalam) adalah sebangun, maka luas bingkai bagian bawah adalah ….

S9

Perhatikan gambar dua bangun yang sebangun di bawah ini.

Jika panjang AB = 18 cm, BC = 12, dan FG = 8 cm, maka luas persegipanjang EFGH = … cm².

S10

Perhatikan gambar berikut.

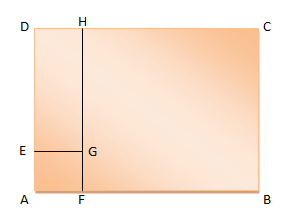
Diketahui AB = 16 cm, BC = 12 cm, dan AE = 3 cm. Persegipanjang ABCD dan AFGE merupakan dua bangun yang sebangun. Luas daerah EGHD adalah … cm².

Share this post