Contoh Soal Pola Bilangan

Contoh Soal Pola Bilangan - Seperti namanya, pola bilangan genap merupakan pola bilangan yang tersusun dari bilangan genap yang dimulai dari angka 2.

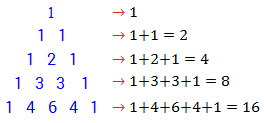
2, 4, 6, 8, 10, ....

Nah, bilangan ke-$n$ dari susunan bilangan yang menggunakan pola bilangan genap adalah $2n$.

Pola bilangan ganjil merupakan pola bilangan yang tersusun dari bilangan ganjil yang dimulai dari angka 1.

1, 3, 5, 7, 9, ....

Nah, bilangan ke-$n$ dari susunan bilangan yang menggunakan pola bilangan ganjil adalah $2n-1$.

Pernakah kalian melihat susunan persegi?

Persegi pada urutan kedua dan ketiga dibentuk dengan cara menumpuk beberapa persegi kecil dari urutan pertama.

Jika kalian amati, persegi pada urutan kedua terdiri atas 4 persegi kecil, sedangkan persegi pada urutan ketiga terdiri atas 9 persegi kecil.

Coba tebak, berapa jumlah persegi kecil pada urutan keempat?

Oleh karena

• banyak persegi kecil pada urutan pertama adalah 1 = 12
• banyak persegi kecil pada urutan kedua adalah 4 = 22
• banyak persegi kecil pada urutan ketiga adalah 9 = 32

maka dapat kita simpulkan bahwa banyak persegi kecil pada urutan ke-$n$ adalah $n^2$.

Nah, sekarang kalian sudah dapat menjawab pertanyaan di atas bukan?

Berdasarkan rumus di atas, dapat kita simpulkan bahwa susunan bilangan yang menggunakan pola bilangan persegi adalah 1, 4, 9, 16, 25, ....

Pola Bilangan Persegipanjang

Pada gambar di atas, persegipanjang pada urutan kedua dan ketiga dibentuk dengan cara menumpuk beberapa persegi kecil.

Jika kalian perhatikan,

• banyak persegi kecil pada urutan pertama adalah 2 = 1 $\times$ 2
• banyak persegi kecil pada urutan kedua adalah 6 = 2 $\times$ 3
• banyak persegi kecil pada urutan ketiga adalah 12 = 3 $\times$ 4

maka dapat kita simpulkan bahwa banyak persegi kecil pada urutan ke-$n$ adalah $n\times (n+1)$.

Susunan bilangan yang menggunakan pola bilangan persegipanjang adalah 2, 6, 12, 20, ....

Apakah kalian masih ingat dengan bentuk segitiga Pascal?

Seperti yang telah kalian ketahui, segitiga Pascal pertama kali diperkenalkan oleh ilmuwan Prancis bernama Blaise Pascal pada tahun 1653.

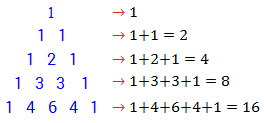
Nah, jika semua angka pada setiap baris kita jumlahkan, maka akan kita peroleh susunan bilangan berikut: 1, 2, 4, 8, 16, ....

Nah, karena

• $1=2^0$
• $2=2^1$
• $4=2^2$
• $8=2^3$
• $16=2^4$

maka bilangan ke-$n$ dari susunan bilangan tersebut adalah $2^{n-1}$.

Bilangan Fibonacci ditemukan oleh Leonardo Fibonacci, seorang ilmuwan dari Italia.

1, 1, 2, 3, 5, 8, 13, ...

Nah, bilangan Fibonacci dimulai dari dua buah bilangan, kemudian bilangan selanjutnya ditentukan dengan cara menjumlahkan dua bilangan sebelumnya.

Bilangan selanjutnya dari suatu susunan bilangan aritmetika ditentukan dengan menjumlahkan atau mengurangkan bilangan sebelumnya dengan suatu bilangan tertentu.

2, 6, 10, 14, ...

• Bilangan selanjutnya diperoleh dengan menjumlahkan bilangan sebelumnya dengan bilangan 4.

18, 15, 12, 9, ...

• Bilangan selanjutnya diperoleh dengan mengurangkan bilangan sebelumnya dengan bilangan 3.

Bilangan selanjutnya dari suatu susunan bilangan geometri ditentukan dengan mengalikan bilangan sebelumnya dengan suatu bilangan tertentu.

2, 6, 18, 54, ...

• Bilangan selanjutnya diperoleh dengan mengalikan bilangan sebelumnya dengan angka 3.

48, 24, 12, 6, ...

• Bilangan selanjutnya diperoleh dengan mengalikan bilangan sebelumnya dengan bilangan $\frac{1}{2}$.

S1

Diketahui susunan bilangan sebagai berikut: 1, 4, 9, 16, 25, ..... Susunan bilangan tersebut mengikuti pola bilangan ....

S2

Susunan bilangan berikut ini yang menggunakan pola bilangan Fibonacci adalah ....

S3

15, 11, 7, ..., ..., ...

Tiga bilangan yang sesuai untuk melengkapi susunan bilangan di atas adalah ....

S4

Banyak lingkaran pada urutan ke-9 adalah ....

S5

Tiga bilangan yang sesuai untuk melanjutkan susunan bilangan 0,04 ; 0,2 ; 1; ... adalah ....

S6

Susunan bilangan berikut ini yang menggunakan pola bilangan persegipanjang adalah ....

S7

Jumlah semua angka pada baris ke-$n$ dari segitiga Pascal adalah ....

S8

Diantara susunan bilangan berikut, yang tidak menggunakan pola bilangan geometri adalah ....

S9

Tiga bilangan yang sesuai untuk melanjutkan susunan bilangan 11, 13, 17, 23, ... adalah ....

S10

Tiga bilangan selanjutnya dari susunan bilangan 5, 6, 9, 14, ... adalah ....

Share this post