Nilai Nilai Optimum dari Program Linear

Nilai Nilai Optimum dari Program Linear - Pada topik sebelumnya kalian telah belajar tentang penyelesaian sistem pertidaksamaan linear dua variabel. Dalam pembahasan model matematika sistem pertidaksamaan linear dua variabel kalian telah mempelajari cara menyusun model matematika yang berkaitan dengan masalah nyata program linear.

Nilai Nilai Optimum dari Program Linear

Dari model matematika tersebut akan dicari nilai dan yang memenuhi kendala-kendala dan menyebabkan fungsi objektif maksimum atau minimum sesuai dengan pertanyaannya.

Metode yang dapat dipakai dalam menentukan nilai optimum adalah:
1) metode uji titik pojok
2) metode garis selidik
3) metode simpleks

Dalam pembahasan kali ini kalian akan diajak untuk menggunakan metode uji titik pojok dalam menentukan nilai optimum.

Titik pojok adalah titik-titik yang terletak pada sudut dari daerah penyelesaian sistem pertidaksamaan linear dua variabel. Langkah-langkah dalam menentukan nilai optimum dengan metode uji titik pojok adalah:
1) Tetapkan fungsi kendala dari model matematika program linear.
2) Gambarlah daerah penyelesaian.
3) Tetapkan titik-titik pojoknya.
4) Tentukan nilai fungsi objektif pada setiap titik pojok.
5) Bandingkan nilai-nilai tersebut, nilai terbesar adalah nilai maksimum fungsi objektif dan nilai terkecil adalah nilai minimum fungsi objektif.

Contoh 1 :

Tentukan nilai maksimum dari f(x,y) = 2x + 5y yang memenuhi kendala : 
7x + 3y ≤ 21, x ≥ 0, dan y ≥ 0

Pembahasan :

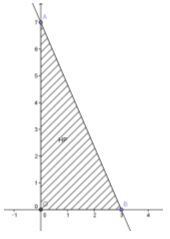
Gambar grafik himpunan penyelesaian dari fungsi kendala adalah sebagai berikut :

Berdasarkan gambar di atas, titik pojok daerah himpunan penyelesaian adalah :
(0,0) , (0,7), dan (3,0)

Dengan demikian, 
1. f(0,0) = 2.0 + 5.0 = 0
2. f(0,7) = 2.0 + 5.7 = 35
3. f(3,0) = 2.3 + 5.0 = 6

Jadi, nilai maksimum dari fungsi obyektif f(x,y) = 2x + 5y dengan kendala di atas adalah 35.

Contoh 2 :

Tentukan nilai maksimum dari f(x,y) = 6x - 4y yang memenuhi kendala : 
x - y ≤ 0, x + y ≥ 3, x + y ≤ 5 dan x ≥ 4

Pembahasan :

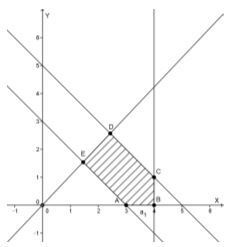
Gambar grafik himpunan penyelesaian dari fungsi kendala di atas adalah sebagai berikut :

Berdasarkan gambar di atas, titik pojok daerah himpunan penyelesaian adalah :
(3,0) , (4,0) , (4,1) , (5/2 , 5/2) , dan (3/2 , 3/2)

Dengan demikian,
1. f(3,0) = 6.3 - 4.0 = 18
2. f(4,0) = 6.4 - 4.0 = 24
3. f(4,1) = 6.4 - 4.1 = 20
4. f(5/2 , 5/2) = 6.(5/2) - 4.(5/2) = 5
5. f(3/2 , 3/2) = 6.(3/2) - 4.(3/2) = 3

Jadi, nilai maksimum dari fungsi obyektif f(x,y) = 6x - 4y dengan kendala di atas adalah 24.

Contoh 3 :

Untuk menghasilkan barang A diperlukan bahan baku 20 kg dan waktu kerja mesin 2 jam. Untuk barang B diperlukan bahan baku 30 kg dan waktu kerja mesin 1 jam. Bahan baku yang tersedia 240 kg, sedangkan waktu kerja mesin 16 jam. Jika barang A dijual dengan harga 
Rp 400.000,00 dan barang B dijual dengan harga Rp 3.000,00. Tentukan pendapatan maksimum yang diperoleh dari penjualan dua barang tersebut!

Pembahasan :

Model matematika dari masalah di atas adalah sebagai berikut :

Memaksimumkan : f(x,y) = 400.000x + 300.000y
dengan fungsi kendala :
1. 20x + 30y ≤ 240 <=> 2x + 3y ≤ 24 
2. 2x + y ≤ 16
3. x ≥ 0
4. y ≥ 0

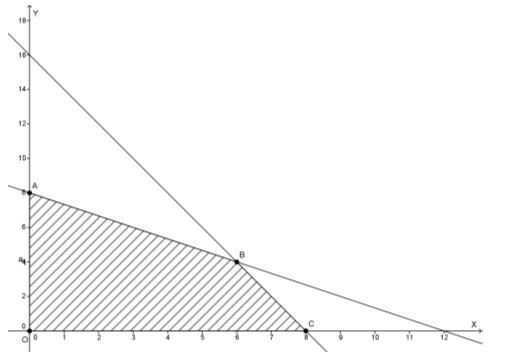
Dengan demikian, gambar grafik himpunan penyelesaian dari fungsi kendala di atas adalah :

Berdasarkan gambar di atas, titik pojok daerah himpunan penyelesaian adalah :
(0,0) , (0,8) , (6,4) , dan (8,0)

Dengan demikian,
1. f(0,0) = 400.000 (0) + 300.000 (0) = 0
2. f(0,8) = 400.000 (0) + 300.000 (8) = 2.400.000
3. f(6,4) = 400.000 (6) + 300.000 (4) = 3.600.000
4. f(8,0) = 400.000 (8) + 300.000 (0) = 3.200.000

Jadi, pendapatan maksimumnya adalah Rp3.600.000,00

Share this post