Contoh Soal Barisan Aritmetika

Contoh Soal Barisan Aritmetika - barisan bilangan diperoleh dari susunan bilangan yang teratur dan mengikuti pola tertentu.

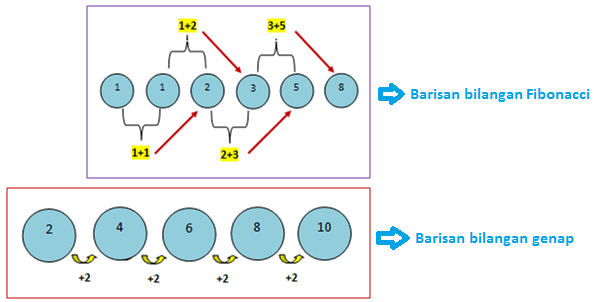
Berikut ini adalah contoh barisan bilangan:

• barisan bilangan Fibonacci : 1, 1, 2, 3, 5, 8, …
• barisan bilangan genap : 2, 4, 6, 8, 10, …

Kedua contoh di atas sama-sama merupakan barisan bilangan, namun kedua barisan tersebut memiliki karakter yang berbeda.

Dapatkah kalian menebak apa perbedaan karakter antara kedua barisan bilangan di atas?
Yuk kita amati ilustrasi berikut ini.

Dari ilustrasi di atas, tampak bahwa selisih antara dua suku yang berurutan pada barisan Fibonacci tidaklah bernilai tetap, sedangkan selisih antara dua suku yang berurutan pada barisan bilangan genap bernilai tetap, yaitu 2.

Nah, oleh karena karakter yang demikianlah, maka barisan bilangan genap termasuk ke dalam barisan aritmetika.

Jadi, apa yang dimaksud dengan barisan aritmetika?

Secara umum, barisan aritmetika didefinisikan sebagai barisan bilangan dimana selisih antara dua bilangan yang berurutan selalu bernilai tetap (konstan).

Barisan aritmetika memiliki pola sebagai berikut: 
a , (a + b) , (a + 2b) , ... , (a + (n - 1)b)

Bilangan pertama, kedua, ketiga, dan ke-n dari barisan di atas berturut-turut dinamakan suku pertama, suku ke-2, suku ke-3, dan suku ke-n. Adapun selisih antara dua suku yang berurutan dinotasikan dengan b dan dikenal dengan istilah beda antar suku atau beda.

Jika Un dan Un - 1 berturut-turut menyatakan suku ke-n dan suku ke-n - 1, maka b = Un - Un - 1.

Beda antar suku dari Um dan Un juga dapat ditentukan dengan rumus berikut $b=\frac{U_m-U_n}{m-n}$. Perlu kalian ketahui, rumus ini biasanya digunakan untuk mencari beda antar suku jika kedua suku yang diketahui tidak berurutan.

RUMUS SUKU KE-n DAN SUKU TENGAH

Jika kita hendak mencari nilai suku ke-n, dimana nilai n relatif besar, maka perhitungan secara manual dengan melanjutkan pola barisan tentu akan membutuhkan banyak waktu. Nah, oleh karena itu kita perlu menentukan rumus suku ke-n dari suatu barisan aritmetika.

Berdasarkan pola dari barisan aritmetika, dapat kita simpulkan bahwa rumus suku ke-n adalah Un = a + (n - 1)b.

Apakah suku tengah dari suatu barisan aritmetika juga dapat ditentukan?
Ya, tentu saja dapat.

Jika Ut menyatakan suku tengah dari suatu barisan aritmetika, maka $U_t=\frac{\left(a+U_n\right)}{2}$.

S1

Berikut ini yang merupakan cara untuk menentukan beda antar suku pada suatu barisan aritmetika adalah ….

S2

Jika rumus suku ke–n dari suatu barisan aritmetika adalah $U_n=3+\left(n-1\right)\times 5$, maka suku pertama dari barisan tersebut adalah ….

S3

Jika rumus suku ke-n suatu barisan aritmetika adalah $U_n=5-\left(n-1\right)\times 7$, maka beda antar suku dari barisan tersebut adalah ….

S4

Beda antar suku dari suatu barisan aritmetika dengan 
U4 = 6 dan U10 = 42 adalah ….

S5

3, 5, 7, … ,15

Suku tengah dari barisan aritmetika di atas adalah ….

S6

Suku ke-5 dan suku ke-9 dari suatu barisan aritmetika berturut-turut adalah 8 dan 20. Suku pertama barisan tersebut adalah ….

S7

Rumus suku ke-n dari barisan aritmetika 9, 7, 5, 3, … adalah ….

S8

Diketahui rumus suku ke-n suatu barisan aritmetika adalah Un = 7n - 3. Jika suku ke-n dari barisan tersebut adalah 60, maka nilai n adalah ….

S9

Diketahui barisan aritmetika 2, 6, 10, 14, … , 74. 
Banyak suku pada barisan tersebut adalah ….

S10

Diketahui suatu barisan aritmetika 21, 18, 15, 12, …. 
Suku ke-15 dari barisan tersebut adalah ….

Share this post