Contoh Soal Barisan Geometri
Contoh Soal Barisan Geometri - Seperti yang telah kalian ketahui, barisan aritmetika merupakan barisan bilangan dimana selisih antara dua suku yang berurutan selalu tetap.

Contoh 1:
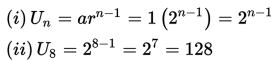
Contoh 2:
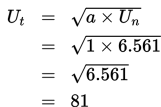
Tahukah kalian bahwa selain barisan aritmetika, ada pula barisan geometri?
Apa itu barisan geometri dan apa perbedaannya dengan barisan aritmetika?
Apa itu barisan geometri dan apa perbedaannya dengan barisan aritmetika?
Sebelum menjawab pertanyaan di atas, yuk kita amati dua contoh barisan bilangan berikut:
- 1, 2, 3, 4, 5, …
- 1, 2, 4, 8, 16, …

Jika kita perhatikan pola dari kedua barisan di atas, tampak bahwa
- beda antar suku pada barisan bilangan di sebelah kiri nilainya tetap, yaitu 1
- beda antar suku pada barisan bilangan di sebelah kanan nilainya tidak tetap, akan tetapi rasio antara dua suku yang berurutan nilainya tetap, yaitu 2
Nah, pada contoh di atas, barisan bilangan di sebelah kiri disebut barisan aritmetika, sedangkan barisan bilangan di sebelah kanan disebut barisan geometri.
Dengan demikian, dapat disimpulkan bahwa barisan U1, U2, U3, ... , Un - 1, Un disebut barisan geometri jika untuk setiap bilangan asli n berlaku .
Lebih lanjut,
- suku pertama dinotasikan U1 atau a
- suku ke-n dinotasikan dengan Un
- rasio dinotasikan dengan r
RUMUS SUKU KE-n DAN SUKU TENGAH
Berdasarkan pola dari barisan geometri, suku ke-n suatu barisan geometri dapat ditentukan dengan menggunakan rumus: Un = arn - 1.
Apakah suku tengah juga dapat ditentukan?
Ya, tentu saja.
Ya, tentu saja.
Jika suatu barisan geometri mempunyai n suku, maka suku tengah dari suatu barisan tersebut adalah , dimana aadalah suku pertama dan Un adalah suku terakhir dari barisan tersebut.
CONTOH
Nah, supaya kalian lebih paham mengenai barisan geometri, yuk kita perhatikan bersama contoh-contoh berikut ini.
Contoh 1:
Diberikan deret geometri: 1, 2, 4, 8, 16, ….
Tentukan suku ke-8 dari barisan di atas.
Tentukan suku ke-8 dari barisan di atas.
Penyelesaian:
Suku pertama dan rasio dari barisan di atas berturut-turut adalah
- U1 = a = 1
Dengan demikian,
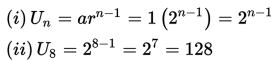
Jadi, suku ke-8 dari barisan 1, 2, 4, 8, 16, … adalah 128.
Contoh 2:
Diberikan deret geometri: 1, 3, 9, …. , 6.561.
Tentukan suku tengah dari barisan di atas.
Tentukan suku tengah dari barisan di atas.
Penyelesaian:
Suku pertama dan suku terakhir dari barisan di atas berturut-turut adalah
- U1 = a = 1
- Un = 6.561
Dengan demikian,
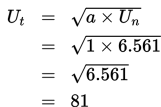
Jadi, suku tengah dari barisan di atas adalah 81.
S1
Perbandingan antara dua suku yang berurutan pada barisan geometri disebut ….
S2
Berikut ini yang merupakan barisan geometri adalah ….
S3
3, a , 27, -81, 243, …
Agar barisan di atas menjadi barisan geometri, maka nilai a adalah ….
S4
Rasio pada barisan geometri: 48, 24, 12, 6, 3, … adalah ….
S5
-2, 8, -32, 128, -512, …
Rasio dari barisan geometri di atas adalah ….
S6
3, 6, 12, 24, 48, …
Suku ke-10 dari barisan geometri di atas adalah ….
S7
Diketahui suatu barisan geometri 7, 14, 28, 56, … , 7.168. Banyak suku bilangan pada barisan tersebut adalah ….
S8
Suku tengah dari barisan geometri 2, 4, 8, 16, … , 512 adalah ….
S9
Diketahui suku ke-3 dan suku ke-6 pada suatu barisan geometri berturut-turut adalah 45dan 1.215. Jika rasio bernilai positif, maka suku ke-2 dari barisan tersebut adalah ….
S10
Diketahui barisan geometri 8, 16, 32, 64, ….
Rumus suku ke-n dari barisan tersebut adalah ….
Rumus suku ke-n dari barisan tersebut adalah ….
