Contoh Soal Deret Aritmetika

Contoh Soal Deret Aritmetika - Sebelum mempelajari lebih lanjut tentang deret aritmetika, ada baiknya kita mengingat kembali mengenai barisan aritmetika. Apakah kamu masih ingat tentang barisan aritmetika? Pada topik sebelumnya telah disampaikan bahwa secara umum barisan aritmetika dapat didefinisikan sebagai barisan bilangan dengan selisih antara dua suku yang berurutan selalu tetap. Selisih antara dua suku yang berurutan pada barisan aritmetika dikenal dengan istilah “beda antarsuku” atau “beda”. Barisan aritmetika memiliki pola sebagai berikut.

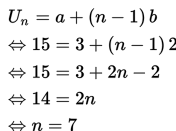
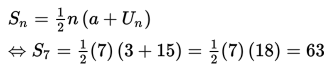
              $U_1$, $U_2$, $U_3$, ... $U_n$= a, a + b, a + 2b, a + 3b, ... a + (n - 1) b

Dengan, 
a = $U_1$ = suku pertama
b = beda antar suku
a + b = $U_2$ = suku kedua
a + 2b = $U_3$ = suku ketiga
a + 3b = $U_4$ = suku keempat
a + (n - 1)b = $U_n$ = suku ke-n

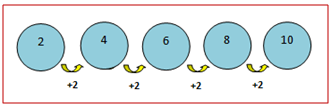
Perhatikan gambar di bawah ini.

Dari ilustrasi di atas diperoleh informasi bahwa suku pertama barisan tersebut adalah adalah a = 2 dan selisih antarsukunya adalah b = 2.

       Lalu, apa kaitan antara barisan aritmetika dengan deret aritmetika? Jika $U_1$, $U_2$, $U_3$, ... $U_n$ adalah suku-suku barisan aritmetika, maka $U_1$ + $U_2$ + $U_3$ + ... $U_n$ disebut dengan deret aritmetika. Jadi, suku-suku dari suatu deret aritmetika berasal dari barisan aritmetika. Dengan kata lain, deret aritmetika merupakan jumlah suku-suku suatu barisan aritmetika.

       Bagaimana cara menentukan jumlah n suku pertama suatu deret aritmetika? Apakah sukunya harus dijumlahkan satu persatu? Meskipun bisa dijumlahkan, cara tersebut pasti akan sangat merepotkan. Terutama jika n suku pertamanya cukup banyak, misal 100 atau 200 suku pertama. Selain itu, cara tersebut juga membutuhkan ketelitian yang tinggi supaya kita tidak salah menghitung, namun jangan khawatir karena kamu dapat menentukan jumlah n suku pertama deret aritmetika dengan menggunakan rumus:

                     $S_n$ = $\frac{1}{2}$ n (a + $U_n$) atau $S_n$ = $\frac{1}{2}$ n (2a + (n - 1) b)

Untuk suku ke-n suatu deret aritmetika dapat ditentukan dengan rumus,
                     $U_n$ = $S_n$ - $S_{n-1}$

Kamu juga dapat menggunakan rumus suku ke-n pada barisan aritmetika yaitu,
                     $U_n$ = a + (n - 1) b

Supaya kamu semakin paham, ayo perhatikan contoh-contoh berikut ini.

Contoh 1

Hitunglah jumlah dari deret artimetika 3 + 5 + 7 + ... + 15.

Penyelesaian:
Diketahui deret aritmetika 3 + 5 + 7 + ... + 15.

Dari deret tersebut diperoleh informasi bahwa, a = 3, b = 2 dan $U_n$ = 15.

Mula-mula tentukan nilai n-nya, agar kita dapat menggunakan rumus $S_n$ = $\frac{1}{2}$ n (a + $U_n$).

Cara untuk menentukan nilai n adalah sebagai berikut.

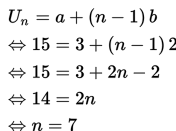
Ternyata, 15 adalah suku ke 7 ($U_7$) atau nilai n = 7,

Selanjutnya, tentukan hasil penjumlahan ketujuh suku ($S_7$) dari 1 + 3 + 7 + ... + 15 dengan mengganti a = 3, $U_n$ = 15 dan n = 7 ke $S_n$.

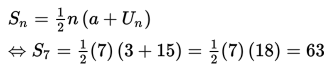
Jadi, jumlah dari 3 + 5 + 7 + ... + 15 adalah 63.

S1

Berikut ini yang merupakan deret aritmetika adalah ….

S2

Pernyataan yang benar tentang deret aritmetika 18 + 14 + 10 + 6 + … adalah …

S3

Jumlah n suku pertama deret aritmetika -9 - 7 - 5 - 3 - … ditentukan oleh rumus ....

S4

Jumlah sepuluh suku pertama dari deret aritmetika 3 + 7 + 11 + 15 + … adalah ....

S5

Jumlah delapan suku pertama dari deret aritmetika -2 - 4 - 6 - 8 - … adalah ….

S6

Jumlah dari 1 + 5 + 9 + 13 + … + 37 adalah ….

S7

Jumlah dari 2 + 5 + 8 + 11 + … + 35 adalah ….

S8

Jumlah n suku pertama suatu deret aritmetika ditentukan oleh rumus Sn = 3n2 + n . Suku pertama dari deret tersebut adalah ….

S9

Jumlah n suku pertama suatu deret aritmetika ditentukan oleh rumus Sn = 5n2 - 7n . Suku ke-5 dari deret tersebut adalah ….

S10

Jumlah n suku pertama suatu deret aritmetika ditentukan oleh rumus Sn = 2n2 - 6n . Suku ke-10 dari deret tersebut adalah ….

Share this post