Menyelesaikan SPLDV dengan Menggunakan Determinan

Menyelesaikan SPLDV dengan Menggunakan Determinan - Pada topik sebelumnya, kalian telah belajar tentang cara menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV) dengan menggunakan invers matriks. Kalian tentu sudah paham bukan? Pada topik ini, kalian masih akan belajar tentang cara menyelesaikan SPLDV, tetapi dengan menggunakan determinan.

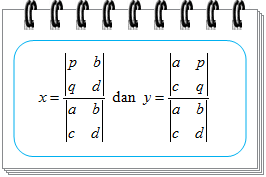
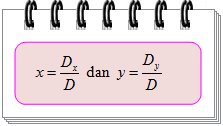
Menyelesaikan SPLDV dengan Menggunakan Determinan

Determinan merupakan suatu bilangan yang berkaitan dengan elemen-elemen diagonal utama dan elemen-elemen diagonal samping sebuah matriks. Determinan hanya berlaku pada matriks persegi, misalnya pada matriks ordo 2 x 2 seperti yang telah kalian pelajari sebelumnya. Pemahaman kalian tentang determinan tersebut akan sangat membantu kalian dalam mempelajari topik ini, untuk itu mari kita ingat kembali.

Setelah mengingat kembali tentang determinan, sekarang mari perhatikan ilustrasi berikut ini.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Pak Rahmat membeli 3 buah apel dan 2 buah jeruk seharga Rp8.000,00. Di tempat yang sama, Bu Rahmat membeli 1 buah apel dan 2 buah jeruk seharga Rp4.000,00. Berapakah harga 1 buah apel dan 1 buah jeruk?

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

        Kalian tentu telah mampu menyelesaikan permasalahan tersebut dengan menggunakan invers matriks. Lantas, bagaimana jika kita ingin menyelesaikannya dengan menggunakan determinan? Untuk mengetahuinya, mari pelajari dahulu uraian beikut ini.

🍎 KONSEP

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Misalkan terdapat sistem persamaan linear dua variabel berikut.

ax+by=pcx+dy=q$\begin{array}{l}ax+by=p\\ cx+dy=q\end{array}$

Dengan metode eliminasi, diperoleh:

ax+by=pcx+dy=q∣∣∣×c×a∣∣∣acx+bcy=pcacx+ady=qa⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯$\begin{array}{l}ax+by=p\\ cx+dy=q\end{array}|\begin{array}{l}\times c\\ \times a\end{array}|\begin{array}{l}acx+bcy=pc\\ \underset{\_}{acx+ady=qa}\end{array}\begin{array}{l}\\ \underset{\_}{}\end{array}$

                                  bcy−ady(bc−ad)yyy======pc−qapc−qapc−qabc−ad−(−pc+qa)−(−bc+ad)qa−pcad−bc∣∣∣∣acpq∣∣∣∣∣∣∣∣acbd∣∣∣∣$\begin{array}{rll}bcy-ady& =& pc-qa\\ \left(bc-ad\right)y& =& pc-qa\\ y& =& \frac{pc-qa}{bc-ad}\\ & =\end{array}$

$\begin{array}{r}\frac{-\left(-pc+qa\right)}{-\left(-bc+ad\right)}\\ & =& \frac{qa-pc}{ad-bc}\\ y& =& \frac{\left|\begin{array}{ll}a& p\\ c& q\end{array}\right|}{\left|\begin{array}{ll}a& b\\ c& d\end{array}\right|}\end{array}$

Dengan cara yang sama, didapatkan nilai x:

x=pd−qbad−bc=∣∣∣∣pqbd∣∣∣∣∣∣∣∣acbd∣∣∣∣$x=\frac{pd-qb}{ad-bc}=\frac{\left|\begin{array}{cc}p& b\\ q& d\end{array}\right|}{\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|}$

Dari penjelasan di atas, dapat disimpulkan bahwa nilai x dan y dapat dicari dengan cara berikut.

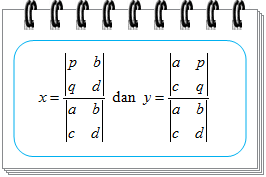
Metode di atas disebut dengan metode determinan atau aturan Cramer yang dirumuskan sebagai berikut.

Misalkan terdapat sistem persamaan linear berikut.

ax+by=pcx+dy=q$\begin{array}{l}ax+by=p\\ cx+dy=q\end{array}$

Jika disajikan dalam bentuk matriks, maka diperoleh:

(acbd)(xy)=(pq)$\left(\begin{array}{ll}a& b\\ c& d\end{array}\right)\left(\begin{array}{l}x\\ y\end{array}\right)=\left(\begin{array}{l}p\\ q\end{array}\right)$

Misalkan matriks A = (acbd)$\left(\begin{array}{ll}a& b\\ c& d\end{array}\right)$ dan matriks B = (pq)$\left(\begin{array}{l}p\\ q\end{array}\right)$ .

Nilai x$x$ dan y$y$ dapat ditentukan dengan aturan Cramer berikut.

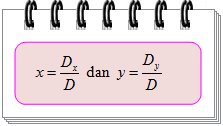
Keterangan:

❶ D=ad−bc$D=ad-bc$ adalah determinan matriks A.

❷ Dx=pd−qb$D_x=pd-qb$ adalah determinan matriks A yang kolom pertamanya diganti dengan elemen matriks B.

❸ Dy=aq−cp$D_y=aq-cp$ adalah determinan matriks A yang kolom keduanya diganti dengan elemen matriks B.

Setelah memahami konsep tersebut, mari kita selesaikan permasalah pada ilustrasi di atas dengan menggunakan metode determinan.

Misalkan:

x$x$ = harga apel

y$y$ = harga jeruk

Sistem persamaan linear dua variabel yang terbentuk dari ilustrasi tersebut adalah:

3x+2y=8000x+2y=4000$\begin{array}{l}3x+2y=8000\\ x+2y=4000\end{array}$

Kemudian, ubah sistem persamaan linear tersebut menjadi persamaan matriks berikut.

(3122)(xy)=(80004000)$\left(\begin{array}{ll}3& 2\\ 1& 2\end{array}\right)\left(\begin{array}{l}x\\ y\end{array}\right)=\left(\begin{array}{l}8000\\ 4000\end{array}\right)$

Selanjutnya, tentukan tentukan nilai D$D$, Dx$D_x$, dan Dy$D_y$.

D$D$ merupakan determinan dari matriks (3122)$\left(\begin{array}{cc}3& 2\\ 1& 2\end{array}\right)$ .

D=∣∣∣3122∣∣∣=(3.2)−(2.1)=6−2=4$\begin{array}{ll}D& =\left|\begin{array}{ll}3& 2\\ 1& 2\end{array}\right|\\ & =\left(3.2\right)-\left(2.1\right)\\ & =6-2\\ & =4\end{array}$

Dx$D_x$ merupakan determinan matriks (3122)$\left(\begin{array}{ll}3& 2\\ 1& 2\end{array}\right)$ yang kolom pertamanya diganti dengan (80004000)$\left(\begin{array}{l}8000\\ 4000\end{array}\right)$.

Dx=∣∣∣8000400022∣∣∣=(8000.2)−(2.4000)=16000−8000=8000$\begin{array}{ll}{D}_x& =\left|\begin{array}{ll}8000& 2\\ 4000& 2\end{array}\right|\\ & =\left(8000.2\right)-\left(2.4000\right)\\ & =16000-8000\\ & =8000\end{array}$

Dy$D_y$ merupakan determinan matriks (3122)$\left(\begin{array}{ll}3& 2\\ 1& 2\end{array}\right)$ yang kolom keduanya diganti dengan (80004000)$\left(\begin{array}{l}8000\\ 4000\end{array}\right)$.

Dy=∣∣∣3180004000∣∣∣=(3.4000)−(8000.1)=12000−8000=4000$\begin{array}{ll}{D}_y& =\left|\begin{array}{ll}3& 8000\\ 1& 4000\end{array}\right|\\ & =\left(3.4000\right)-\left(8000.1\right)\\ & =12000-8000\\ & =4000\end{array}$

Dengan menggunakan aturan Cramer, nilai x$x$ dan y$y$ dapat ditentukan sebagai berikut.

x=DxD=80004=2000$\begin{array}{ll}x& =\frac{D_x}{D}\\ & =\frac{8000}{4}\\ & =2000\end{array}$

y=DyD=40004=1000$\begin{array}{ll}y& =\frac{D_y}{D}\\ & =\frac{4000}{4}\\ & =1000\end{array}$

Jadi, harga 1 buah apel adalah Rp2.000,00 dan harga 1 buah jeruk adalah Rp1.000,00.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Mudah bukan? Agar kalian lebih paham lagi, perhatikan contoh berikut ini.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Tentukan himpunan penyelesaian dari sistem persamaan berikut dengan metode determinan.

3x−y=162x+5y=5$\begin{array}{l}3x-y=16\\ 2x+5y=5\end{array}$

Jawab:

Mula-mula, nyatakan SPLDV tersebut dalam bentuk matriks berikut.

(32−15)(xy)=(165)$\left(\begin{array}{ll}3& -1\\ 2& 5\end{array}\right)\left(\begin{array}{l}x\\ y\end{array}\right)=\left(\begin{array}{l}16\\ 5\end{array}\right)$

Kemudian, tentukan D$D$, Dx$D_x$, dan Dy$D_y$.

D=∣∣∣32−15∣∣∣=(3.5)−(−1.2)=15−(−2)=15+2=17$\begin{array}{ll}D& =\left|\begin{array}{ll}3& -1\\ 2& 5\end{array}\right|\\ & =\left(3.5\right)-\left(-1.2\right)\\ & =15-\left(-2\right)\\ & =15+2\\ & =17\end{array}$

Dx=∣∣∣165−15∣∣∣=(16.5)−(−1.5)=80−(−5)=80+5=85$\begin{array}{ll}{D}_x& =\left|\begin{array}{cc}16& -1\\ 5& 5\end{array}\right|\\ & =\left(16.5\right)-\left(-1.5\right)\\ & =80-\left(-5\right)\\ & =80+5\\ & =85\end{array}$

Dy=∣∣∣32165∣∣∣=(3.5)−(16.2)=15−(32)=−17$\begin{array}{ll}{D}_y& =\left|\begin{array}{ll}3& 16\\ 2& 5\end{array}\right|\\ & =\left(3.5\right)-\left(16.2\right)\\ & =15-\left(32\right)\\ & =-17\end{array}$

Dengan menggunakan aturan Cramer, nilai x$x$ dan y$y$ dapat ditentukan sebagai berikut.

x=DxD=8517=5$x=\frac{D_x}{D}=\frac{85}{17}=5$

y=DyD=−1717=−1$y=\frac{D_y}{D}=\frac{-17}{17}=-1$

Jadi, himpunan penyelesaian sistem persamaan linear tersebut adalah {5,-1}.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Nah, kalian telah selesai belajar tentang cara menyelesaikan SPLDV dengan menggunakan determinan. Sekarang, saatnya kalian mengasah kemampuan dengan mengerjakan latihan soal-soal berikut ini. Selamat berlatih.

Share this post