Contoh Soal Peluang Komplemen Suatu Kejadian

Contoh Soal Peluang Komplemen Suatu Kejadian - Peluang Suatu Kejadian

Jika banyak titik sampel pada kejadian K adalah n (K) dan banyak anggota ruang sampel kejadian K adalah n (S), maka peluang kejadian K dapat dinyatakan dengan:

P(K)=n(K)n(S)$P(K)=\frac{n(K)}{n(S)}$

Kisaran nilai peluang adalah 0 ≤ P (K) ≤ 1. Ini berarti, kejadian yang mustahil memiliki nilai P (K) = 0 dan kejadian yang mutlak terjadi memiliki nilai P (K) = 1.

Mari simak ilustrasi berikut.

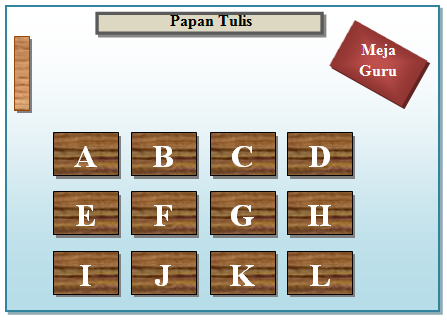
Sebuah kelas memiliki susunan tempat duduk seperti pada gambar di bawah ini. Tempat duduk setiap siswa ditentukan secara acak.

Misalkan K adalah kejadian seorang siswa duduk pada baris terdepan. Ruang sampel K adalah seluruh tempat duduk siswa yaitu {A, B, C, D, E, F, G, H, I, J K, L}, sehingga n (S) = 12. Titik sampel K adalah tempat duduk baris terdepan yaitu {A, B, C, D}, sehingga n (K) = 4. Kejadian seorang siswa duduk bukan pada baris terdepan disebut komplemen kejadian K dan dilambangkan dengan Kc . Titik sampel Kc yaitu {E, F, G, H, I, J, K, L} dengan n (Kc ) = 8.

       Dari gambar di atas diperoleh bahwa banyak tempat duduk pada baris terdepan dan bukan pada baris terdepan sama dengan banyak tempat duduk siswa yang ada di kelas tersebut yaitu 4 + 8 = 12 tempat duduk. Jika dikaitkan dengan banyak kejadian K, Kc , dan anggota ruang sampel, maka diperoleh:

n(K)+n(Kc)=n(S)$n(K)+n(K^c)=n(S)$

Untuk memperoleh peluangnya, maka n (K) dan n (Kc ) harus dibagi dengan n (S).
n(K)n(S)+n(Kc)n(S)=n(S)n(S)$\frac{n(K)}{n(S)}+\frac{n(K^c)}{n(S)}=\frac{n(S)}{n(S)}$
⇔ P(K)+P(Kc)=1$P(K)+P(K^c)=1$

Berdasarkan persamaan peluang di atas, jumlah peluang kejadian yang saling berkomplemen adalah 1.

Berdasarkan hasil uraian di atas, maka diperoleh kesimpulan sebagai berikut.

Peluang Komplemen Suatu Kejadian

Jika Kc adalah komplemen dari K, maka berlaku:

P (Kc ) = 1 - P (K)

dengan P (K) adalah peluang kejadian K dan P (Kc ) adalah peluang komplemen kejadian K.

Catatan: 
Komplemen suatu kejadian K disebut juga dengan lawan kejadian K atau kejadian bukan K.

SOAL 1

Pada percobaan melempar sebuah dadu bersisi 6, komplemen dari kejadian muncul mata dadu 4 atau 6 adalah ....

SOAL 2

Diketahui peluang seseorang datang terlambat adalah 0,3. Peluang ia datang tepat waktu adalah ....

SOAL 3

Jika banyak anggota ruang sampel E dinyatakan dengan n (S) = 20 dan banyak titik sampel E dinyatakan n (E) =12, maka nilai P (Ec ) adalah ....

SOAL 4

Menurut sebuah survei, dari selusin lampu pijar ditemukan 10 lampu tidak mengalami cacat. Maka peluang ditemukannya lampu yang cacat adalah ....

SOAL 5

Dari 1, 2, 3, 4, 5 akan disusun bilangan 3 angka berbeda. Peluang terbentuk bilangan yang tidak habis dibagi 5 adalah ....

SOAL 6

Kejadian A dan Ac saling berkomplemen dan memiliki peluang masing-masing 2n–14n$\frac{2n–1}{4n}$ dan 4n–34n$\frac{4n–3}{4n}$. Nilai P (Ac ) adalah ....

SOAL 7

Adel dan Bayu adalah dua siswa yang mengikuti tes. Jika peluang Adel dan Bayu untuk lulus berturut-turut adalah 0,4 dan 0,75, maka peluang Adel lulus, tetapi Bayu tidak lulus adalah ....

SOAL 8

Peluang seseorang gagal memenangkan undian adalah 911$\frac{9}{11}$. Jika total seluruh kupon undian adalah 132 kupon, maka banyak kupon yang dimiliki orang tersebut adalah ... kupon.

SOAL 9

Terdapat 10 pintu gerbang pada sebuah gelanggang. Peluang seseorang masuk dan keluar gelanggang tidak pada gerbang yang sama adalah ....

SOAL 10

Dalam sebuah kantong terdapat 5 bola kuning, 6 bola merah dan 3 bola hijau. Jika akan diambil 2 bola sekaligus dari kantong, peluang terambil bola merah baik salah satu atau keduanya adalah ....

Share this post