Contoh Soal Menyelesaikan Masalah Nyata Terkait Ellips
Contoh Soal Menyelesaikan Masalah Nyata Terkait Ellips - Dalam topik ini kalian akan belajar tentang bagaimana cara mengolah data dan menganalisis model matematika menggunakan operasi aljabar untuk menyelesaikan masalah nyata yang berkaitan dengan ellips.
Definisi Ellips
Unsur-Unsur Ellips
Contoh Nyata Terkait Ellips
Persamaan Ellips
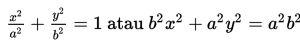

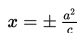
untuk ellips yang fokusnya di sumbu X
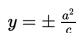
untuk ellips yang fokusnya di sumbu Y

2. Ellips dengan pusat (p,q)

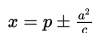
untuk ellips yang fokusnya di sumbu X
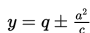
untuk ellips yang fokusnya di sumbu Y
Dalam bentuk baku, persamaan umum ellips dengan pusat (p,q) dapat ditulis sebagai berikut :
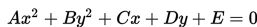
dengan ketentuan :
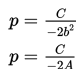
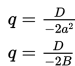
Contoh 1
Berapa panjang kabel yang menghubungkan lampu 1 dan 3 serta lampu 1 dan 2 (dalam ratusan meter)?
Solusi :
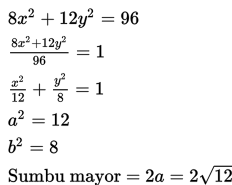
Jadi, panjang kabel yang menghubungkan antara lampu 2 dan 4 adalah :
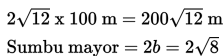
Jadi, panjang kabel yang menghubungkan antara lampu 1 dan 3 adalah :

Contoh 2
Solusi :
Persamaan umum ellips :
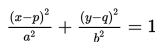
Dengan demikian, persamaan ellips tersebut adalah :
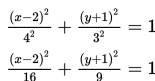
Dengan kata lain, persamaan orbit planet tersebut adalah :
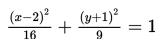
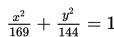
Mari kita mengenali ellips melalui definisi, unsur, dan contoh benda nyata berbentuk ellips, serta persamaan ellips berikut.
Definisi Ellips
Ellips adalah tempat kedudukan titik – titik pada bidang datar yang jumlah jaraknya terhadap dua titik tertentu selalu sama. Kedua titik tersebut selanjutnya disebut fokus.
Unsur-Unsur Ellips
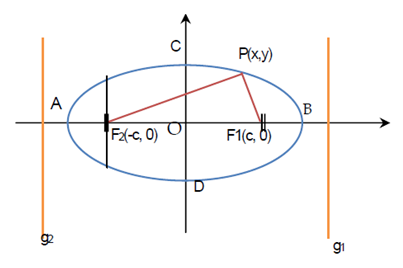
Definisi ellips di atas selanjutnya dapat diperlihatkan melalui gambar dan unsur-unsur ellips berikut :

Pada ellips di atas, sumbu horisontal adalah sumbu X dan sumbu vertikal adalah sumbu Y.
• F1 (c, 0) dan F2 (-c, 0) adalah fokus ellips
• Garis yang memuat fokus, (garis AB) disebut sumbu panjang (sumbu mayor)
• Garis melalui titik tengah kedua fokus dan tegak lurus terhadap sumbu panjang (garis CD) disebut sumbu pendek (sumbu minor)
• Titik potong kedua sumbu : O(0,0) disebut pusat ellips
• Titik potong ellips dengan kedua sumbu disebut puncak ellips ( A, B, C, D )
• g1 dan g2 = garis direktriks
Contoh Nyata Terkait Ellips
Dalam kehidupan sehari-hari, ada banyak contoh benda berbentuk ellips yang dapat kita temui.
Apa saja bentuk ellips tersebut?
Apa saja bentuk ellips tersebut?
1. Orbit revolusi planet
Planet-planet dalam tata surya mengelilingi matahari melalui lintasan (orbit) berbentuk ellips.
2. Ellipse Park
Ellipse Park terletak antara Gedung Putih dan Monumen Washington, di Washington DC. Taman tersebut dikelilingi oleh sebuah jalan berbentuk ellips.
3. Litotripsi
Litotripsi merupakan suatu prosedur medis yang dilakukan untuk menghancurkan batu di saluran kemih dengan menggunakan gelombang kejut ultrasonik sehingga pecahannya dapat dengan mudah lolos dari tubuh. Alat yang digunakan untuk prosedur ini lithotripter, berbentuk setengah elips 3 dimensi mengaplikasikan sifat-sifat dari titik fokus elips, digunakan untuk mengumpulkan gelombang ultrasonik pada satu titik fokus untuk dikirimkan ke batu ginjal yang terletak di titik fokus lainnya.
Persamaan Ellips
Ellips dengan pusat (0,0)
Persamaan ellips dengan pusat (0,0) adalah :
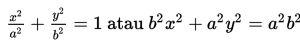

Pada ellips di atas, sumbu horisontal adalah sumbu X dan sumbu vertikal adalah sumbu Y.
• Koordinat Fokus F1 (c, 0 ) dan F2 ( -c, 0 ) dengan c2 = a2 – b2
• Koordinat puncak A(-a, 0), B(a, 0), C(0, b), dan D(0, -b)
• Sumbu panjang (mayor) = 2a dan sumbu pendek (minor) = 2b
• Perbandingan jarak dari titik pada ellips ke titik focus dengan jarak titik ke garis direktris disebut eksentrisitas (e), e = c/a dengan 0 < e < 1
• Persamaan garis direktrik ellips adalah :
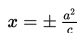
untuk ellips yang fokusnya di sumbu X
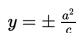
untuk ellips yang fokusnya di sumbu Y
Bentuk umum persamaan ellips di atas jika diilustrasikan maka akan menjadi ellips yang fokusnya di sumbu X. Adapun ellips yang fokusnya di sumbu Y, persamaannya menjadi :

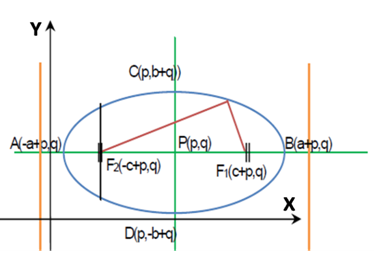
2. Ellips dengan pusat (p,q)
Persamaan ellips dengan pusat (p,q) adalah :


Pada ellips di atas, sumbu horisontal adalah sumbu X dan sumbu vertikal adalah sumbu Y.
• Koordinat Fokus F1 (c+p,q) dan F2(-c+p,q) dengan c2 = a2 – b2
• Koordinat puncak A(-a+p,q); B(-a+p,q); C(p,b+q) dan D(p,-b+q).
• Sumbu panjang (mayor) = 2a dan sumbu pendek (minor) = 2b.
• Persamaan garis direktrik ellips adalah :
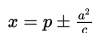
untuk ellips yang fokusnya di sumbu X
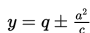
untuk ellips yang fokusnya di sumbu Y
Dalam bentuk baku, persamaan umum ellips dengan pusat (p,q) dapat ditulis sebagai berikut :
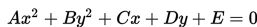
dengan ketentuan :
• A = b2
• B = a2
• C = -2pb2
• D = -2qa2
• B = a2
• C = -2pb2
• D = -2qa2
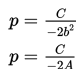
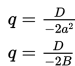
Dengan demikian, pusat ellips dari bentuk baku di atas adalah (C/-2A , D/-2B) dan E = p2 b2 + q2 a2 – a2 b2
Selanjutnya, untuk mengetahui bagaimana unsur-unsur ellips dan persamaannya dapat digunakan, mari kita simak contoh berikut :
Contoh 1
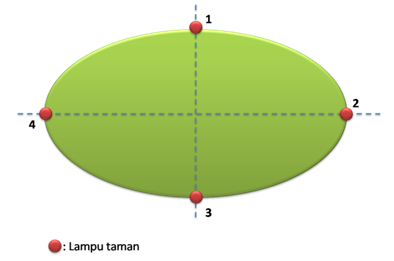
Sebuah taman berbentuk ellips, dengan persamaan tepinya adalah 8x2 + 12y2 = 96. Di tepi taman tersebut akan dipasang 4 lampu taman, dengan posisi seperti gambar berikut :

Berapa panjang kabel yang menghubungkan lampu 1 dan 3 serta lampu 1 dan 2 (dalam ratusan meter)?
Solusi :
Kabel yang menghubungkan lampu 1 dan 3 mewakili sumbu minor ellips, sedangkan lampu yang menghubungkan lampu 2 dan 4 mewakili sumbu mayor ellips. Karena itu, untuk menghitung panjang kabel yang dimaksud, cukup dengan menetukan panjang sumbu mayor dan sumbu minor ellips.
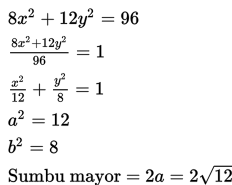
Jadi, panjang kabel yang menghubungkan antara lampu 2 dan 4 adalah :
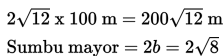
Jadi, panjang kabel yang menghubungkan antara lampu 1 dan 3 adalah :

Contoh 2
Orbit sebuah planet digambarkan pada bidang koordinat. Matahari sebagai pusat revolusi palnet terletak pada koordinat ( 2,-1 ), panjang sumbu-sumbunya masing-masing 8dan 6 satuan panjang. Tentukan persamaan orbit planet tersebut.
Solusi :
- Titik pusat ellips (2,-1), maka p = 2, q = -1
- Panjang sumbu mayor = 2a = 8, a =4
- Panjang sumbu minor = 2b = 6, b =3
Persamaan umum ellips :
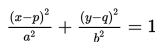
Dengan demikian, persamaan ellips tersebut adalah :
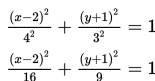
Dengan kata lain, persamaan orbit planet tersebut adalah :
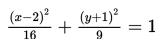
S1
Sketsa sebuah taman berbentuk ellips dibuat pada bidang koordinat dengan persamaan:
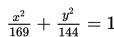
Pada titik fokus taman tersebut, akan dipasang air mancur. Koordinat kedua air mancur tersebut adalah…
S2
Sebuah bak mainan berbentuk elips dengan persamaan tepi bak 20x2 + 36y2 = 720. Jika di kedua puncaknya dipasang patung mainan, jarak kedua patung mainan tersebut adalah …
S3
Sebuah model planet berevolusi pada orbit yang persamaannya 49x2 + 25y2 = 1225. Koordinat salah satu titik terjauh revolusi planet tersebut adalah adalah …
S4
Orbit sebuah planet digambarkan pada sebuah bidang koordinat. Matahari terletak di O (0, 0).Puncak (10, 0) dan (-10, 0) serta salah satu fokusnya (-6, 0). Persamaan orbit tersebut adalah …
S5
Sebuah kolam renang berbentuk ellips. Pusat kolam dianggap sebagai titiik koordinat (0,0). Panjang sumbu mayor dan minornya masing-masing 16 dan 12 satuan panjang. Persamaan tepi kolam tersebut adalah …
S6
Pada titik fokus sebuah taman berbentuk ellips, akan dipasang lampu taman. Persamaantepi taman 9x2 + 25y2 + 18x – 100y = 116 maka koordinat lampu taman adalah…
S7
Meja tamu sebuah rumah berbentuk persamaannya 4x2 + 9y2 – 24x – 36y + 36 = 0. Meja tersebut akan dipasangi taplak dengan hiasan pita di sepanjang sumbu utamanya. Panjang pita yang dibutuhkan adalah …
S8
Orbit sebuah miniatur planet mempunyai persamaan 3x2 + 5y2 – 24x + 30y + 23 = 0. Planet mencapai jarak terjauh dari matahari pada koordinat …
S9
Persamaan orbit planet pada miniatur tata surya yang mataharinya terletak pada koordinat (-1,1) dengan panjang sumbu 8 dan 6 satuan , serta sumbu mayornya sejajar sumbu x adalah ….
S10
Pada sketsa rancangan sebuah taman, lampu taman diletakkan pada ujung sumbu mayor dan minor dengan koordinat (-3,-1) dan (1,2); sumbu mayor sejajar sumbu x, dan berpusat di (1,-1), maka persamaannya adalah ….
