Contoh Soal Menyelesaikan Masalah Nyata Terkait Hiperbola

Contoh Soal Menyelesaikan Masalah Nyata Terkait Hiperbola - Pada topik sebelumnya, kalian telah mempelajari tentang persamaan hiperbola dan persamaan garis singgung hiperbola. Pada topik kali ini, kalian akan mempelajari penerapannya dalam menyelesaikan masalah nyata. Sebelum mempelajarinya, mari kita ingat kembali persamaan-persamaan yang berkaitan dengan hiperbola.

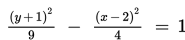
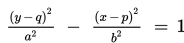
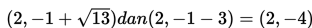
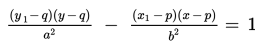
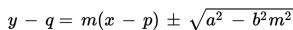
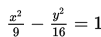
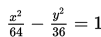
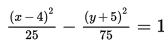
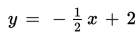
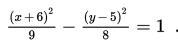
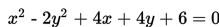
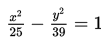
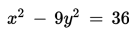
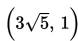
1. Hiperbola Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola. Contoh persamaan hiperbola adalah

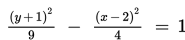
Persamaan hiperbola ini memiliki sumbu utama yang sejajar dengan sumbu y. Rumus bakunya adalah

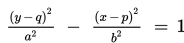
Jadi, a2 = 9 dan b2 = 4 . Akibatnya, c2 = a2 + b2 = 9 + 4 = 13.
Titik pusat hiperbola adalah (2, -1).
Titik puncaknya adalah (2, -1 + 3) = (2, 2) dan (2, -1 – 3) = (2, -4).
Titik fokusnya adalah

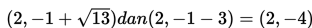
Jika ada garis yang menyinggung hiperbola pada titik R(x1, y1) yang terletak pada hiperbola itu, maka persamaan umum garis singgungnya adalah

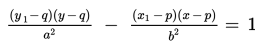
Jika garis yang menyinggung hiperbola itu diketahui gradiennya m, maka persamaan umum garis singgungnya adalah

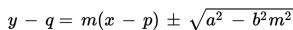
Apakah kalian sudah ingat kembali?

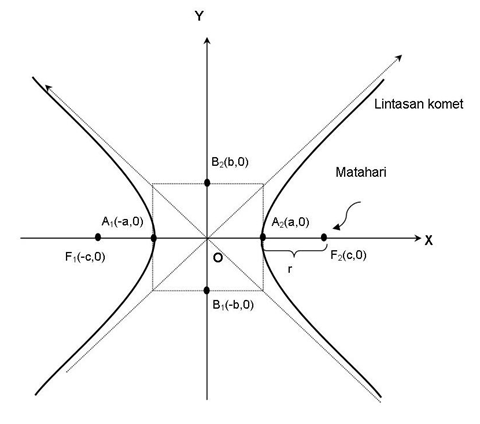
1. Penerapan Hiperbola Persamaan hiperbola dan persamaan garis singgungnya dapat diterapkan dalam menyelesaikan masalah nyata seperti pada contoh berikut. Contoh: Ketika mengajar tentang materi jagat raya, Pak Bima Sakti mengajak siswa-siswanya untuk memeragakan model-model benda langit di laboratorium IPA. Dalam peragaan ini, ia menjelaskan bahwa ada suatu komet yang mengitari matahari dengan lintasan berbentuk hiperbola. Matahari adalah salah satu titik fokusnya. Ia membuat model lintasan itu dengan persamaan 2116x2 – 400y2 = 846400. Menurutmu seberapa dekatkah komet itu dengan matahari? Penyelesaian: Untuk memudahkan menyelesaikan masalah ini, kita dapat menggunakan gambar berikut.

Dalam permasalahan ini, pada dasarnya kita diminta untuk menentukan jarak antara titik fokus dengan titik puncak hiperbola, yaitu r.
Mari kita selesaikan.

Jadi, a = 20 dan b = 46, sehingga c2 = 400 + 2116 => c = 50 
Jarak model komet ke model matahari adalah r = 50 – 20 = 30.

S1

Menurut pengamatan NASA ¬--lembaga pemerintahan Amerika Serikat yang bertanggung jawab terhadap program luar angkasa—terdapat sinar terang yang mengitari dua buah bintang. Sinar ini bergerak dengan lintasan berbentuk hiperbola

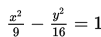
Mereka juga mengamati keberadaan bintang lain pada koordinat (3, 4) di luar berkas sinar itu. Kemudian melalui sistem di monitornya, mereka menarik garis untuk menghubungkan ketiga bintang sehingga membentuk sebuah segitiga. Luas daerah segitiga yang terbentuk adalah ….

S2

Lintasan sebuah meteor mengitari bumi, bentuknya menyerupai hiperbola yang dapat dimodelkan dengan persamaan

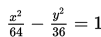
Bumi merupakan salah satu titik fokusnya. Jika semua satuan jarak dalam jutaan mil, maka jarak terdekat meteor tersebut ke bumi adalah ….

S3

Dua buah magnet yang didekatkan saling tolak menolak dengan garis gaya magnet membentuk hiperbola. Lintasan garis gaya itu memenuhi persamaan 16y2 – 4x2 = 64. Nilai eksentisitasnya adalah ….

S4

Seberkas cahaya ditangkap oleh mata. Cahaya ini bergerak dengan lintasan berbentuk hiperbola. Di dalam mata, cahaya yang masuk difokuskan oleh lensa mata dan dijatuhkan ke suatu titik pada retina. Jika lintasan cahaya itu dapat dimodelkan dengan 
persamaan

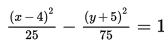
maka jarak antara fokus dan titik pada retina adalah ….

S5

Sebuah komet mengitari dua buah planet dalam lintasan berbentuk hiperbola. Kedua planet itu merupakan titik fokusnya. Menurut pengamatan NASA, kedua titik planet itu berada pada koordinat (7, 1) dan (-3, 1). NASA juga mengamati adanya sebuah sinar yang makin lama makin mendekati lintasan komet itu. Lintasan sinar itu dapat dinyatakan dengan persamaan

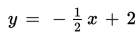
Persamaan lintasan komet adalah ….

S6

Dua orang petani berada pada jarak 8.000 m satu sama lain. Dari tempat mereka berada, mereka melihat orang-orangan sawah disambar oleh petir. Petani pertama yang jaraknya lebih jauh dari orang-orangan sawah, mendengar suara petir 9 detik setelah petani kedua. Jika kecepatan suara 340 m/detik, maka persamaan dari lokasi orang-orangan sawah disambar petir adalah ….

S7

Dua ekor burung terbang dengan lintasan berbentuk hiperbola yang dapat dimodelkan dengan persamaan

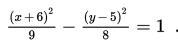
Melihat burung-burung ini, seorang pemburu menembaknya hingga mengenai seekor burung di titik (3, 13). Persamaan lintasan pelurunya adalah …

S8

Sebuah benda langit bergerak dengan lintasan berbentuk hiperbola dengan persamaan

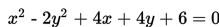
Tiga unit pesawat luar angkasa berusaha mengejarnya. Ketiga pesawat ini terbang sejajar. Lintasan salah satu pesawat berbentuk garis lurus dengan persamaan 2y – x + 3 = 0. Dua buah pesawat lainnya berhasil menyinggung benda langit itu. Lintasan kedua pesawat luar angkasa itu memiliki persamaan …..

S9

Pada hari tertentu, matahari berotasi dalam gerak melingkar. Sinar yang keluar dari titik pada jejak matahari di sundial (jam matahari) berbentuk kerucut. Perpotongan kerucut dengan bidang horizontal dari tanah membentuk bagian berbentuk hiperbola. Jika bentuk tersebut dapat dimodelkan dengan persamaan

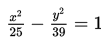
, titik fokusnya adalah ….

S10

Sebuah pesawat tempur bergerak dengan lintasan berbentuk hiperbola yang dapat dimodelkan dengan persamaan

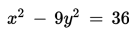
Tiba-tiba seekor burung terbang lurus dan menyinggung pesawat itu pada koordinat

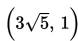
Persamaan lintasan terbangnya burung adalah …..

Share this post