Lingkaran Satuan dan Fungsi - Fungsi Trigonometri 1

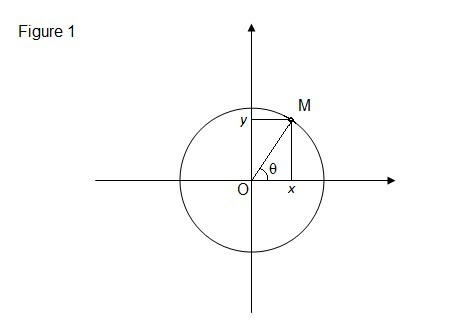
Lingkaran Satuan dan Fungsi - Fungsi Trigonometri 1 - Mari kita definisikan fungsi trigonometri dalam satuan lingkaran (unit circle), seperti terlihat pada gambar di bawah ini. Selanjutnya, dengan memisalkan θ sebagai sudut antara sumbu X dan jari-jari vektor M, maka nilai sinus dan cosinus dapat dihitung dengan cara sebagai berikut :

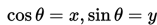
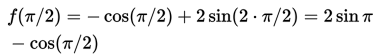
Lingkaran Satuan dan Fungsi - Fungsi Trigonometri 1

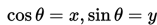
dimana x dan y adalah koordinat titik M.

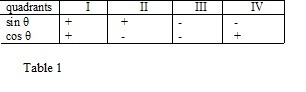
Mari kita definisikan tanda dari nilai sinus dan cosinus pada setiap kuadran.

Persamaan cosθ=x$\cos \theta =x$ mengimplikasikan bahwa tanda cosinus sama dengan tanda absis dari titik M. Sedangkan persamaansinθ=y$\sin \theta =y$ mengimplikasikan bahwa tanda sinus sama dengan tanda ordinat dari titik M. Berdasarkan alasan inilah, dapat dibentuk tabel sebagai berikut :

Contoh 1.

Bagaimanakah tanda dari bentuk berikut ini? 

cos2π3⋅sin5π4$$\cos \frac{2\pi }{3}\cdot \sin \frac{5\pi }{4}$$

?

Jawaban :

Ada 5 sudut istimewa yang menandai setiap kuadran, yaitu : 

0,π/2,π,3π/2,2π.$\mathrm{0,}\pi /\mathrm{2,}\pi ,3\pi /2\mathrm{,2}\pi .$

Jika kita dapat menemukan nilai cosinus dan sinus dari sudut-sudut istimewa, maka hal itu akan sangat menguntungkan. Selanjutnya, dengan bantuan figure 1, maka diperoleh :

1. θ =0 mengimplikasikan bahwa M mempunyai koordinat x=1, y=0. Oleh karena itu, 

sinθ=0,cosθ=1$\sin \theta =\mathrm{0,}\cos \theta =1$

2. θ=pi/2 mengimplikasikan bahwa M mempunyai koordinat x=0, y=1. Oleh karena itu, sin θ=1, cos θ=0.

3. θ=pi mengimplikasikan bahwa M mempunyai koordinat x=-1, y=0. Oleh karena itu, sin θ=0, cos θ=-1.

4. θ=3pi/2 mengimplikasikan bahwa M mempunyai koordinat x=0, y=-1. Oleh karena itu, sin θ=-1, cos θ=0.

5. θ=pi. Hal yang sama juga terjadi pada item#1.

Contoh 2.

Carillah nilai dari funggsi trigonometri : f(θ)=-cos θ+2sin (2θ) jika   θ=pi/2 .

Penyelesaian :

Dengan mensubtitusikan  θ=pi/ kedalam f(θ), diperoleh : 

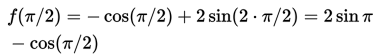
 Selanjutnya, dengan menggunakan nilai cosinus dan sinus untuk sudut pi dan pi/2, diperoleh :  f(pi/2)=0.

Share this post