Contoh Soal Pengenalan Teorema Pythagoras
Contoh Soal Pengenalan Teorema Pythagoras - Pernahkah kalian dan teman-teman bermain voli di halaman rumah? Saat bermain voli, adakalanya bola kalian tersangkut di atap rumah. Jika itu terjadi, apa yang akan kalian lakukan?
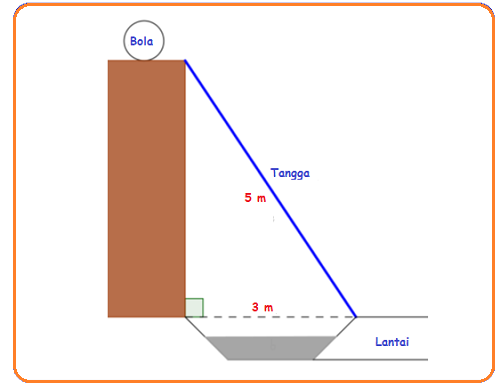


Misalkan bola voli kalian tersangkut di atap rumah yang bawahnya terdapat selokan air selebar 3 m. Kalian memutuskan untuk mengambilnya menggunakan tangga. Ternyata, tangga sepanjang 5 m sudah cukup untuk memanjat atap tersebut. Pertanyaanya, bisakah kalian menentukan tinggi rumah itu tanpa mengukurnya? Tahukan kalian hubungan antara panjang tangga, lebar selokan, dan tinggi rumah tersebut? Untuk mengetahui jawabannya, mari simak uraian berikut.
Dalam ilmu Matematika, kita bisa mengetahui tinggi suatu benda dengan menggunakan teorema yang berlaku pada segitiga siku-siku. Teorema tersebut dinamakan dengan teorema Pythagoras.
Tahukah Kamu?
Teorema Pythagoras sebenarnya telah dikenal dan digunakan berabad-abad sebelum kelahiran Pythagoras. Pythagoras adalah seorang filsuf asal Yunani yang hidup sekitar abad ke-6 Sebelum Masehi (SM). Di Cina, teorema Pythagoras disebut dengan Gougo Teorema. Teorema ini juga telah dibukukan oleh Baudhayana Sulba Sutra asal India lengkap dengan bukti geometrisnya. Namun, baru pada masa Pythagoras lah teorema ini dapat dibuktikan secara matematis sehingga dinamakan dengan teorema Pythagoras.
Pemikiran Pythagoras tidak lepas dari kaumnya yang dikenal dengan kaum Pythagorean. Akan tetapi, ketika muridnya yang bernama Hippasus menemukan bilangan irrasional dari sisi miring segitiga siku-siku sama kaki, Phytagoras bersama kaumnya memutuskan untuk membunuh Hippasus karena tidak dapat menyangkal bukti yang diajukannya.
Beberapa konsep yang mendukung penemuan teorema Pythagoras adalah:
a. Luas persegi
Suatu persegi dengan panjang sisi a mempunyai luas L = a x a = a2 .
b. Luas segitiga
Suatu segitiga dengan alas a dan tinggi t mempunyai luas .
c. Kuadrat jumlah suku aljabar
Pada suku aljabar (a + b), berlaku (a + b)2 = a2 + 2ab + b2 .
Nah, untuk memahami tentang teorema Pythagoras, perhatikan ilustrasi gambar di bawah ini.

Kita dapat menentukan luas persegi di atas dengan dua cara, yaitu:
a. Menghitung luas persegi besar dengan ukuran sisi (a + b).
Luas persegi dengan ukuran sisi (a + b) adalah L = (a + b)2 = a2 + 2ab + b2 .
b. Menghitung luas 4 segitiga siku-siku dan luas 1 persegi kecil dengan ukuran sisi c pada bagian tengah bangun.
Luas 4 segitiga adalah .
Luas 1 persegi kecil adalah .
Luas total adalah .
Kedua cara di atas, tentu akan menghasilkan nilai yang sama, sehingga dapat kita tuliskan:
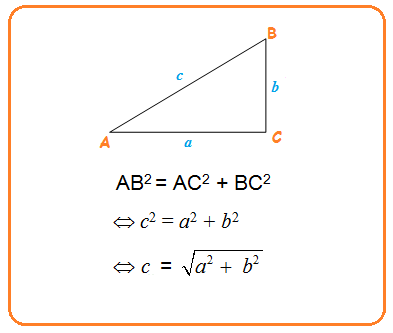
Perhatikan bahwa a adalah panjang alas, b adalah tinggi, dan c adalah sisi miring pada segitiga siku-siku. a dan b merupakan dua sisi yang saling tegak lurus yang disebut sisi siku-siku, sedangkan c merupakan sisi di hadapan sudut siku-siku yang disebut dengan hipotenusa atau sisi miring. Dari hasil kesamaan di atas, diperoleh bahwa:
Untuk setiap segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi siku-sikunya.

Nah, sifat inilah yang dinamakan dengan teorema Pythagoras.
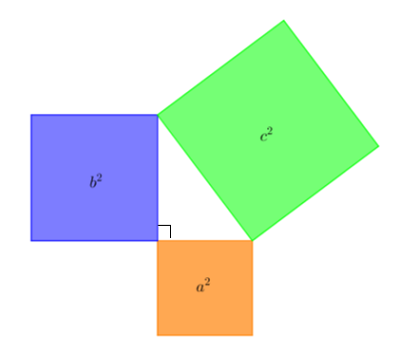
Kebenaran teorema Pythagoras juga dapat diketahui dengan menempatkan persegi di setiap sisi segitiga siku-siku seperti berikut.

Misalkan kita memiliki persegi A, B, dan C yang masing-masing berukuran a, b, dan c. Luas masing-masing persegi adalah La = a2 , Lb = b2 , dan Lc = c2 . Jika a = 3 cm, b = 4 cm, dan c = 5 cm, kita akan mendapatkan bahwa:
Luas persegi pada sisi miring = jumlah luas persegi pada kedua sisi siku-sikunya
Lc = La + Lb
⇔c2 = a2 + b2
⇔52 = 32 + 42
⇔25 = 9 + 16
Contoh 1
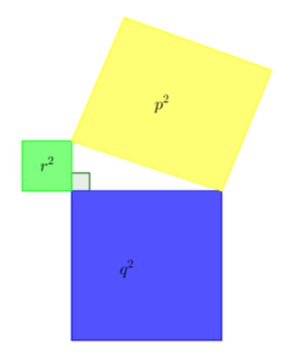
Perhatikah ilustrasi gambar di bawah ini.

Hubungan antara luas ketiga persegi adalah ....
Jawab:
Berdasarkan teorema Pythagoras, luas persegi pada sisi miring sama dengan jumlah luas persegi pada kedua sisi siku-sikunya. Oleh karena p merupakan sisi miring serta r dan q merupakan sisi siku-sikunya, maka berlaku:
Jadi, hubungan antara ketiga persegi tersebut adalah .
Contoh 2
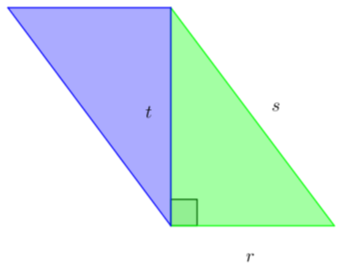
Diketahui sebuah jajargenjang dengan alas r dan tinggi t.

Hubungan panjang sisi yang benar adalah ....
Jawab:
Perhatikan segitiga berwarna hijau. Oleh karena segitiga tersebut adalah segitiga siku-siku, maka kuadrat sisi miringnya sama dengan jumlah kuadrat kedua sisi siku-sikunya.
Diketahui sisi miring dari segitiga tersebut adalah s dan kedua sisi siku-sikunya adalah r dan t, sehingga diperoleh:
Jadi, hubungan panjang sisi yang benar adalah .
Contoh 3
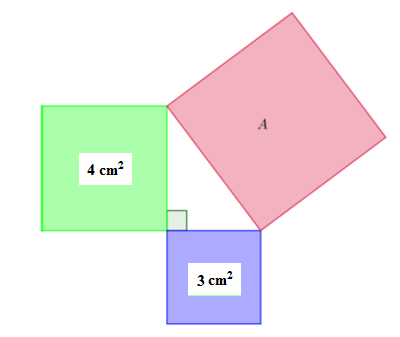
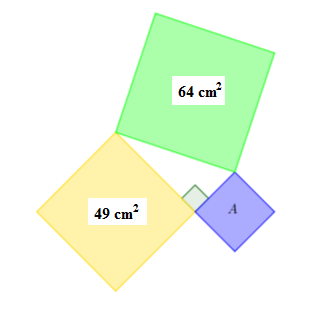
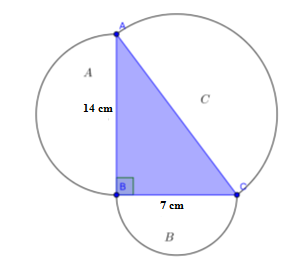
Perhatikah ilustrasi bangun persegi di bawah ini.

Luas persegi A adalah ... cm2 .
Jawab:
Berdasarkan teorema Pythagoras, luas persegi pada sisi miring sama dengan jumlah luas persegi pada sisi siku-sikunya.
Oleh karena A merupakan persegi pada sisi miring, maka:
Luas persegi A = 4 + 3 = 7
Jadi, luas persegi A adalah 7 cm2 .
S1
Pilihan Tunggal
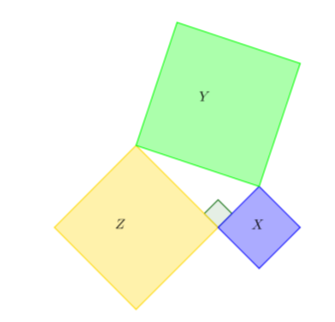
Persegi X memiliki panjang sisi x cm, persegi Y memiliki panjang sisi y cm, dan persegi Z memiliki panjang sisi z cm.

Hubungan luas persegi X, Y, dan Z adalah ....
S2
Pilihan Tunggal
Pada suatu ∆DEF berlaku (DE)2 + (DF)2 = (EF)2 . Hipotenusa dari dari ∆DEF adalah ....
S3
Pilihan Tunggal
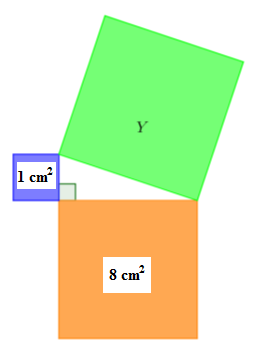
Perhatikan ilustrasi bangun persegi di bawah ini.

Luas persegi Y adalah... cm2 .
S4
Pilihan Tunggal
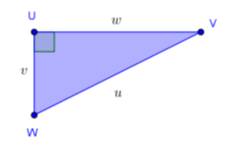
Panjang sisi UV pada segitiga siku-siku berikut ini adalah ....

S5
Pilihan Tunggal
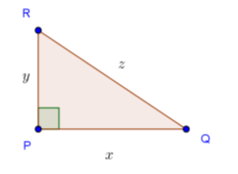
Pada ∆PQR yang siku-siku di P , berlaku PQ = x, PR = y, dan RQ = z.

Rumus Pythagoras yang mewakili bangun tersebut adalah....
S6
Pilihan Tunggal
Perhatikan ilustrasi bangun persegi di bawah ini.

Luas persegi A adalah... cm2 .
S7
Pilihan Tunggal
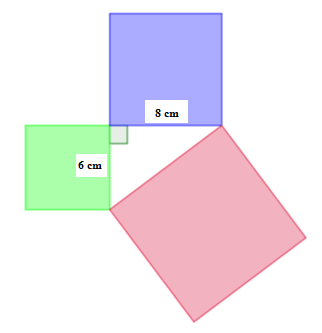
Perhatikah ilustrasi gambar persegi di bawah ini.

Jika persegi biru memiliki panjang sisi 8 cm dan persegi hijau memiliki panjang sisi 6 cm, maka luas persegi merah adalah....cm2 .
S8
Pilihan Tunggal
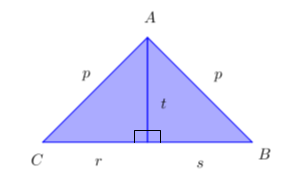
Pada segitiga sama kaki ABC, diketahui garis t adalah garis tinggi.

Pernyataan yang sesuai dengan gambar di atas adalah ....
S9
Pilihan Tunggal
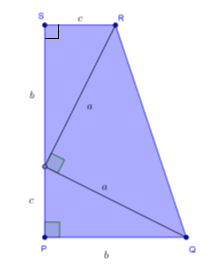
Perhatikan trapesium siku-siku PQRS berikut ini.

Hubungan yang benar antara sisi-sisi bangun tersebut adalah ....
S10
Pilihan Tunggal
Perhatikah ilustrasi gambar persegi di bawah ini.

Luas bangun C adalah ... cm2 .
