Contoh Soal Menentukan Fungsi Kuadrat Jika Diketahui Titik Potong Sumbu x atau y, dan Titik Puncak

Contoh Soal Menentukan Fungsi Kuadrat Jika Diketahui Titik Potong Sumbu x atau y, dan Titik Puncak - Pada topik kali ini kalian akan belajar bagaimana cara menentukan fungsi kuadrat jika diketahui titik potong sumbu 

$X$ atau sumbu $Y$ dan titik puncak.

Apakah kalian masih ingat dengan apa yang dimaksud dengan titik puncak?

Seperti yang telah kalian ketahui, titik puncak adalah titik optimum. Jika parabola membuka ke atas, maka titik puncak parabola merupakan titik minimum, namun jika parabola membuka ke bawah, maka titik puncak parabola adalah titik maksimum.

Untuk memudahkan kalian dalam mempelajari topik ini, yuk kita cermati beberapa contoh soal berikut.

Contoh 1

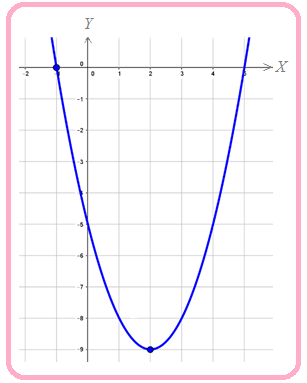
Tentukan fungsi kuadrat dari grafik fungsi berikut.

Penyelesaian:

Misalkan fungsi kuadrat yang dimaksud adalah $f(x)=a{x}^2+bx+c$.

Oleh karena titik puncak grafik fungsi kuadrat adalah $(2,-9)$, maka sumbu simetrinya adalah $x=2$.

Oleh karena koordinat titik potong grafik fungsi dengan sumbu $X$ adalah $(-1,0)$, maka koordinat titik potong dengan sumbu $X$yang lain adalah $(2(2)-(-1),0)=(5,0)$.

Dengan demikian, $f(x)=a(x+1)(x-5)$.

Oleh karena koordinat titik puncak adalah $(2,-9)$, maka

$\begin{array}{l}f\left(2\right)=-9\\ \iff a\left(2+1\right)\left(2-5\right)=-9\\ \iff -9a=-9\\ \iff a=1\end{array}$

Jadi, fungsi kuadrat yang terbentuk adalah

$\begin{array}{lll}f\left(x\right)& =& a\left(x+1\right)\left(x-5\right)\\ & =& 1\left(x+1\right)\left(x-5\right)\\ & =& x^2-4x-5\end{array}$

Contoh 2

Tentukan fungsi kuadrat yang grafiknya memotong sumbu $Y$ di titik $(0,5)$ dan titik puncaknya adalah $(-2,-3)$.

Penyelesaian:

Misalkan fungsi kuadrat yang dimaksud adalah $f(x)=a{x}^2+bx+c$.

Oleh karena koordinat titik potong grafik fungsi dengan sumbu $Y$ adalah $(0,5)$, maka $f(0)=5\iff c=5$.

Akibatnya, $f(x)=a{x}^2+bx+5$.

Oleh karena titik puncak grafik fungsi kuadrat adalah $(-2,-3)$, maka

$\begin{array}{l}f\left(-2\right)=-3\\ \iff a{\left(-2\right)}^2+b\left(-2\right)+5=-3\iff 4a-2b+5=-3\\ \iff 4a-2b=-8\\ \iff 2a-b=-4\end{array}$

Oleh karena sumbu simetrinya adalah $x=-2$, maka

$\begin{array}{l}x=-2\\ \iff -\frac{b}{2a}=-2\\ \iff b=4a\\ \iff 4a-b=0\end{array}$

Selanjutnya, jika kita gunakan metode subtitusi dan eliminasi, kita peroleh bahwa $a=2$ dan $b=8$.

Jadi, fungsi kuadrat yang terbentuk adalah $f(x)=2x^2+8x+5$.

S1

Hubungan antara nilai $a$ dan $b$ pada fungsi kuadrat $f(x)=a{x}^2+bx+c$ yang memiliki titik puncak $(2,-4)$ adalah ....

S2

Fungsi kuadrat $f(x)=a{x}^2+bx+c$ yang memotong sumbu $Y$ di titik $(0,-8)$ dan titik puncaknya adalah $(3,1)$ akan melalui titik ....

S3

Titik puncak suatu fungsi kuadrat adalah $(-4,-10)$, sedangkan titik potongnya dengan sumbu $X$ adalah $(-5,0)$. Titik potong dengan sumbu $X$ yang lain adalah ....

S4

Fungsi kuadrat $f(x)=a{x}^2+bx+c$ yang memotong sumbu $X$ di titik $(-2,0)$ dan memiliki titik puncak $(3,25)$ adalah ....

S5

Jika grafik fungsi kuadrat $f(x)=a{x}^2+bx+c$ memotong sumbu $X$ di titik $(-2,0)$ dan memiliki titik puncak $(-3,-5)$, maka nilai $a$, $b$, dan $c$ berturut-turut adalah ....

S6

Jika grafik fungsi kuadrat $f(x)=a{x}^2+bx+c$ memotong sumbu $X$ di titik $(-2,0)$ dan memiliki titik puncak $(2,16)$, maka nilai $a+b+c$ adalah ....

S7

Fungsi kuadrat $f(x)=a{x}^2+bx+c$ yang memotong sumbu $Y$ di titik $(0,-2)$ dan memiliki titik puncak $(3,7)$ adalah ....

S8

Grafik fungsi kuadrat $f(x)=a{x}^2+bx+c$ memotong sumbu $Y$ di titik $(0,6)$ dan memiliki titik puncak $(1,4)$. Nilai $a$, $b$, dan $c$ berturut-turut adalah ....

S9

Grafik fungsi kuadrat $f(x)=a{x}^2+bx+c$ memotong sumbu $Y$ di titik $(0,8)$ dan memiliki titik puncak $(2,7)$. Nilai dari $4a+2b^2+c$ adalah ....

S10

Fungsi kuadrat yang memotong sumbu $X$ di titik $(6,0)$ dan memiliki titik puncak $(2,8)$ adalah ....

Share this post