Contoh Soal Grafik Fungsi Kuadrat dengan Fungsi Linear yang saling Berpotongan

Contoh Soal Grafik Fungsi Kuadrat dengan Fungsi Linear yang saling Berpotongan - Yuk kita cari tahu apa saja syarat agar fungsi kuadrat dan fungsi linear agar dapat saling berpotongan dan bagaimana cara menentukan koordinat titik potongnya.

Sebagai ilustrasi mengenai kedudukan fungsi kuadrat terhadap fungsi linear, kita akan menggunakan fungsi kuadrat $y=x^2-6x+8$.

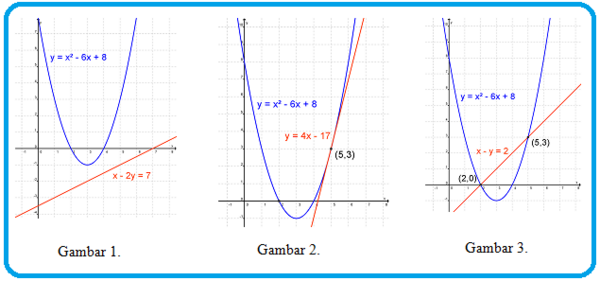
Apa yang dapat kalian simpulkan dari ketiga grafik di atas?

Ya, jika kita perhatikan, ada tiga hal yang dapat kita simpulkan, yaitu:

• grafik fungsi kuadrat $y=x^2-6x+8$ tidak memotong grafik fungsi linear $x-2y=7$
• grafik fungsi kuadrat $y=x^2-6x+8$ bersinggungan dengan grafik fungsi linear $y=4x-17$
• grafik fungsi kuadrat $y=x^2-6x+8$ memotong grafik fungsi linear $x-y=2$ di dua titik yang berbeda

Nah, tahukah kalian mengapa bisa demikian?

Yuk kita analisa gambar 1, 2, dan 3 secara terpisah.

Tidak Berpotongan

Jika kita potongkan grafik fungsi kuadrat $y=x^2-6x+8$ dengan grafik fungsi linear $x-2y=7\iff y=\frac{x-7}{2}$, maka kita peroleh hasil sebagai berikut:

$\begin{array}{lll}{x}^2-6x+8& =& \frac{x-7}{2}\\ \iff 2x^2-12x+16& =& x-7\\ \iff 2x^2-12x+16-x+7& =& 0\\ \iff 2x^2-13x+23& =& 0\end{array}$

Dari persamaan kuadrat di atas, kita ketahui bahwa $a=2$, $b=-13$, dan $c=23$.

Dengan demikian, nilai diskriminan dari $2x^2-13x+23$ adalah sebagai berikut:

$\begin{array}{lll}D& =& b^2-4ac\\ & =& {(-13)}^2-4\left(2\right)\left(23\right)\\ & =& 169-184\\ & =& -15\end{array}$

Nah, karena $D=-15<0$, maka dapat kita simpulkan bahwa grafik fungsi kuadrat dan grafik fungsi linear tidak akan saling berpotongan jika nilai diskriminannya negatif.

Bersinggungan

Jika kita potongkan grafik fungsi kuadrat $y=x^2-6x+8$ dengan grafik fungsi linear $y=4x-17$, maka kita peroleh hasil sebagai berikut:

$\begin{array}{lll}{x}^2-6x+8& =& 4x-17\\ \iff x^2-6x+8-4x+17& =& 0\\ \iff x^2-10x+25& =& 0\end{array}$

Dari persamaan kuadrat di atas, kita ketahui bahwa $a=1$, $b=-10$, dan $c=25$.

Dengan demikian, nilai diskriminan dari $x^2-10x+25$ adalah sebagai berikut:

$\begin{array}{lll}D& =& b^2-4ac\\ & =& {(-10)}^2-4\left(1\right)\left(25\right)\\ & =& 100-100\\ & =& 0\end{array}$

Nah, karena $D=0$, maka dapat kita simpulkan bahwa grafik fungsi kuadrat dan grafik fungsi linear akan saling bersinggungan (berpotongan di satu titik) jika nilai diskriminannya adalah nol.

Berpotongan di Dua Titik

Jika kita potongkan grafik fungsi kuadrat $y=x^2-6x+8$ dengan grafik fungsi linear $x-y=2\iff y=x-2$, maka kita peroleh hasil sebagai berikut:

$\begin{array}{lll}{x}^2-6x+8& =& x-2\\ \iff x^2-6x+8-x+2& =& 0\\ \iff x^2-7x+10& =& 0\end{array}$

Dari persamaan kuadrat di atas, kita ketahui bahwa $a=1$, $b=-7$, dan $c=10$.

Dengan demikian, nilai diskriminan dari $x^2-7x+10$ adalah sebagai berikut:

$\begin{array}{lll}D& =& b^2-4ac\\ & =& {(-7)}^2-4\left(1\right)\left(10\right)\\ & =& 49-40\\ & =& 9\end{array}$

Nah, karena $D=9>0$, maka dapat kita simpulkan bahwa grafik fungsi kuadrat dan grafik fungsi linear akan berpotongan di dua titik jika nilai diskriminannya positif.

Sekarang kalian sudah tahu syarat grafik fungsi kuadrat dan grafik fungsi linear untuk saling berpotongan bukan?

Yuk kita cari tahu bagaimana cara menentukan koordinat titik potong antara grafik fungsi kuadrat dan grafik fungsi linear melalui contoh berikut.

Contoh

Tentukan koordinat titik potong antara grafik fungsi kuadrat $y=-x^2+4x-2$ dan grafik fungsi linear $2x+y=7$.

Penyelesaian:

Langkah pertama adalah menentukan kedudukan grafik fungsi kuadrat terhadap grafik fungsi linear.

Jika kita potongkan grafik fungsi kuadrat $y=-x^2+4x-2$ dengan grafik fungsi linear $2x+y=7\iff y=7-2x$, maka kita peroleh hasil sebagai berikut:

$\begin{array}{lll}-x^2+4x-2& =& 7-2x\\ \iff -x^2+4x-2-7+2x& =& 0\\ \iff -x^2+6x-9& =& 0\end{array}$

Dari persamaan kuadrat di atas, kita ketahui bahwa $a=-1$, $b=6$, dan $c=-9$.

Dengan demikian, nilai diskriminan dari $-x^2+6x-9$ adalah sebagai berikut:

$\begin{array}{lll}D& =& b^2-4ac\\ & =& 6^2-4\left(-1\right)\left(-9\right)\\ & =& 36-36\\ & =& 0\end{array}$

Oleh karena $D=0$, maka grafik fungsi kuadrat $y=-x^2+4x-2$ dan grafik fungsi linear $2x+y=7$ berpotongan di satu titik.

Langkah kedua adalah menentukan koordinat titik potong.

Oleh karena pada langkah pertama sudah ada jaminan bahwa kedua grafik berpotongan, maka untuk menentukan koordinat titik potong, kita perlu menentukan terlebih dahulu nilai $x$ yang memenuhi persamaan $-x^2+6x-9=0$.

$\begin{array}{l}-x^2-6x+9=0\\ \iff x^2+6x-9=0\\ \iff {\left(x-3\right)}^2=0\\ \iff x-3=0\\ \iff x=3\end{array}$

Selanjutnya, jika kita subtitusikan $x=3$ ke persamaan fungsi linear $y=7-2x$, maka $y=7-2(3)=7-6=1$.

Dengan demikian, koordinat titik potong antara grafik fungsi kuadrat $y=-x^2+4x-2$ dan grafik fungsi linear $2x+y=7$adalah $(3,1)$.

S1

Diketahui parabola $y=x^2-6x+8$ dan garis $4x+y=7$. Pernyataan berikut ini yang benar adalah ….

S2

Diketahui parabola $y=-x^2+5x-4$ dan garis $2y–x=5$. Pernyataan berikut ini yang benar adalah ….

S3

Diketahui parabola $y=2x^2-4x+5$ dan garis $2x-y=-1$. Pernyataan berikut ini yang benar adalah ….

S4

Koordinat titik potong antara parabola $y=x^2-5x+4$ dan garis $y=x-1$ adalah ….

S5

Koordinat titik potong antara parabola $y=x^2-4x+3$ dan garis $4x-y=13$ adalah ….

S6

Koordinat titik potong antara parabola $y=-2x^2+4x+6$ dan garis $y=14-4x$ adalah ….

S7

Garis $2x-y=-6$ dan parabola $y=x^2+ax$ berpotongan di dua titik yang berbeda. Pertidaksamaan yang memenuhi adalah ….

S8

Garis $g$ menyinggung parabola $y=2(x-3{)}^2-5$ di titik puncak parabola. Persamaan garis $g$ adalah ….

S9

Garis $y=x+a$ memotong parabola $y=-x^2+6x-5$ di dua titik yang berbeda. Nilai $a$ yang memenuhi adalah ….

S10

Jika garis $y=ax+b$ menyinggung parabola $y=2(x-1{)}^2+3$ di titik $(2,5)$, maka nilai dari $a+b$ adalah ….

Share this post