Contoh Soal Menentukan Fungsi Kuadrat Jika Diketahui Tiga Koordinat Berbeda
Contoh Soal Menentukan Fungsi Kuadrat Jika Diketahui Tiga Koordinat Berbeda - Pada beberapa topik sebelumnya kalian telah belajar tentang bagaimana menggambar grafik fungsi kuadrat. Nah, pada topik kali ini kalian akan belajar tentang bagaimana cara menentukan fungsi kuadrat berbentuk
Kalian tentu masih ingat dengan metode eliminasi dan subtitusi bukan?
Penyelesaian:
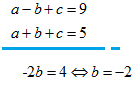
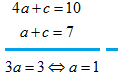
Penyelesaian:
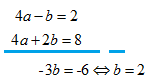
jika diketahui tiga titik yang dilalui oleh grafik fungsinya.
Konsep Dasar
Jika diketahui tiga titik yang dilalui oleh grafik fungsi kuadrat , maka untuk menentukan persamaan fungsi kuadratnya, ada dua langkah yang harus diikuti, yaitu:
- Subtitusikan ketiga titik ke persamaan .
- Tentukan nilai , , dan dengan menggunakan metode eliminasi dan subtitusi.
Kalian tentu masih ingat dengan metode eliminasi dan subtitusi bukan?
Nah, untuk memudahkan kalian dalam memahami topik ini, yuk kita perhatikan beberapa contoh soal berikut.
Contoh 1
Diketahui sebuah grafik fungsi kuadrat melalui titik , , dan . Tentukan fungsi kuadrat yang sesuai.
Penyelesaian:
Misalkan fungsi kuadrat yang dimaksud adalah .
Jika kita subtitusikan titik , , dan ke dalam persamaan di atas, maka akan kita peroleh hasil sebagai berikut:
Selanjutnya, jika kita eliminasi variabel dan dari persamaan (1) dan (2), maka akan kita peroleh hasil sebagai berikut:
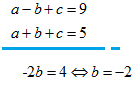
Nah, jika kita subtitusikan hasil di atas ke persamaan (1) dan (3), maka akan kita peroleh sistem persaman linear dua variabel: .
Jika kita eliminasi variabel , maka akan kita peroleh hasil sebagai berikut:
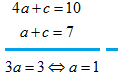
Oleh karena , maka .
Dengan demikian, fungsi kuadrat yang terbentuk adalah .
Contoh 2
Tentukan fungsi kuadrat yang grafiknya melalui titik , , dan .
Penyelesaian:
Misalkan fungsi kuadrat yang dimaksud adalah .
Jika kita subtitusikan ketiga titik yang diketahui dalam soal ke dalam persamaan di atas, maka akan kita peroleh hasil sebagai berikut:
Selanjutnya, jika kita eliminasi variabel dari persamaan (2) dan (3), maka akan kita peroleh hasil sebagai berikut:
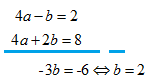
Nah, jika kita subtitusikan hasil di atas ke persamaan (2), maka akan kita peroleh hasil sebagai berikut:
Dengan demikian, fungsi kuadrat yang terbentuk adalah .
S1
Jika grafik fungsi kuadrat melalui titik , maka nilai yang memenuhi adalah ....
S2
Jika grafik fungsi kuadrat melalui titik dan , maka nilai dan berturut-turut adalah ....
S3
Jika grafik fungsi kuadrat melalui titik , maka nilai yang memenuhi adalah ....
S4
Jika grafik fungsi kuadrat melalui titik dan , maka nilai dari adalah ....
S5
Jika grafik fungsi kuadrat melalui titik , , dan , maka nilai , , dan berturut-turut adalah ....
S6
Jika grafik fungsi kuadrat melalui titik , , dan , maka nilai , , dan berturut-turut adalah ....
S7
Fungsi kuadrat yang grafiknya melalui titik , , dan adalah ....
S8
Fungsi kuadrat yang grafiknya melalui titik , , dan adalah ....
S9
Fungsi kuadrat yang grafiknya melalui titik , , dan adalah ....
S10
Fungsi kuadrat yang grafiknya melalui titik , , dan adalah ....
