Contoh Soal Translasi

Contoh Soal Translasi - Translasi merupakan salah satu pokok bahasan dari materi transformasi geometri. Sebelum kita mengenal lebih jauh apa itu translasi, mari kita pahami terlebih dahulu apa itu transformasi geometri.

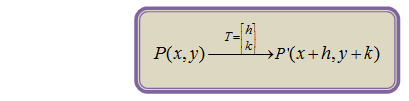
Dalam banyak film-film yang bertema super hero, amati bahwa sebagian besar super hero tersebut dapat berubah dari bentuk manusia biasa menjadi mahluk yang tidak biasa, seperti pada film: Hulk, Transformers, Spiderman, Ultraman, X-man, dan sebagainya. Perubahan bentuk inilah yang disebut dengan "Transformasi".

                                                

        Di dalam geometri juga terdapat proses perubahan bentuk dari bangun-bangun geometri itu sendiri, sehingga disebut dengan "Transformasi Geometri". Perubahan bentuk bangun geometri (transformasi geometri) ini disebabkan oleh adanya perubahan posisi atau formasi dari titik-titik yang membentuk bangun geometri tersebut. Perubahan fomasi tersebut antara lain disebabkan oleh Translasi (perpindahan), Refleksi (pencerminan), Rotasi (perputaran), dan Dilatasi (perubahan ukuran). Semua perubahan tersebut terjadi pada bidang koordinat.

Nah, untuk saat ini mari kita bahas bentuk transformasi geometri yang paling sederhana yaitu Translasi.

☘ Translasi Secara Umum ☘

Secara harfiah translasi dapat diartikan sebagai pergeseran, yaitu perpindahan suatu titik ke titik lainnya dengan menempuh lintasan yang berupa garis lurus.

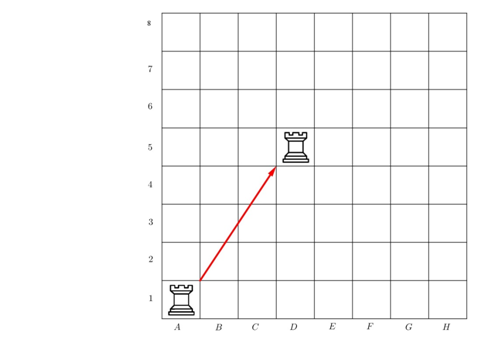
        Perpindahan biji pada permainan catur dapat membantu kamu memahami maksud dari pergeseran ini. Perhatikan gambar perpindahan benteng pada papan catur berikut ini.

        Oleh karena benteng tidak dapat bergerak secara diagonal, maka langkah yang dapat dilakukan untuk menggeser benteng dari posisi A1 ke posisi D5 adalah dengan mula-mula menggeser benteng 3 kotak ke kanan kemudian dilanjutkan dengan 4 kotak ke atas. Langkah dari benteng tersebut dapat dipandang sebagai Translasi dari posisi A1 ke posisi D5. Perpindahan ini dapat dinyatakan dalam bentuk matriks yang disebut "Matriks Translasi/ Matriks Perpindahan". Matriks perpindahan yang bersesuaian dengan pergeseran ini adalah,

                                                                               [34]$\left[\begin{array}{c}3\\ 4\end{array}\right]$

        Namun, bagaimana menyatakan translasi dengan arah sebaliknya? Dengan kata lain, matriks perpindahan seperti apa yang sesuai untuk menyatakan pergeseran benteng dari posisi D5 ke posisi A1? Untuk arah sebaliknya, pemain dapat menggeser benteng 3 kotak ke kiri kemudian dilanjutkan dengan 4 kotak ke bawah. Matriks perpindahan yang bersesuaian dengan pergeseran ini adalah,

                                                                               [−3−4]$\left[\begin{array}{c}-3\\ -4\end{array}\right]$

        Nah, tentunya kamu telah melihat pola urutan yang digunakan dalam pergeseran tersebut bukan? Pergeseran dalam arah horizontal (mendatar) dinyatakan sebagai komponen pertama matriks dan arah vertikal (tegak) dinyatakan sebagai komponen kedua matriks. Arah pergeseran ke kanan dan atas bertanda positif (+) sedangkan pergeseran ke kiri dan bawah bertanda negatif (-).

☘ Translasi Secara Matematis ☘

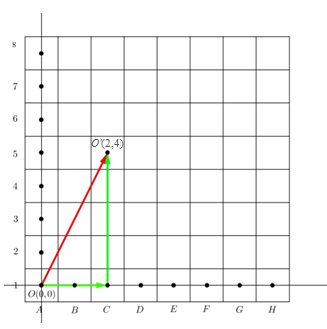
Berdasarkan situasi pegeseran benteng pada ilustrasi papan catur sebelumnya, kita dapat menyusun suatu cara sistematis untuk menyatakan translasi suatu titik secara umum. Misalkan tiap kotak pada papan catur kita nyatakan ulang sebagai titik-titik pada koordinat kartesius yang mana kotak A1 diwakili oleh titik (0,0), B1 diwakili oleh (1,0), C1 diwakili oleh (2,0) dan seterusnya. Perhatikan gambar berikut.

                                        

        Berdasarkan posisi-posisi pada bidang koordinat tersebut, kita dapat mentranslasi titik O(0,0) dengan matriks [24]$\left[\begin{array}{c}2\\ 4\end{array}\right]$ ke titik O’(2,4) yang menunjukkan pergeseran benteng dari A1 ke C5 pada papan catur. Translasi ini dapat dituliskan sebagai berikut:

                                        O(0,0)⟶[24]O′(0+2,0+4)$O(0,0)\stackrel{\left[\begin{array}{c}2\\ 4\end{array}\right]}{⟶}{O}^{\prime }(0+2,0+4)$

Hal yang sama berlaku untuk sebarang titik P(x,y) yang ditranslasi dengan sebarang matriks T=[hk]$T=\left[\begin{array}{c}h\\ k\end{array}\right]$ untuk menghasilkan titik P'(x+h, y+k). Secara matematis hal ini dapat dinyatakan sebagai,

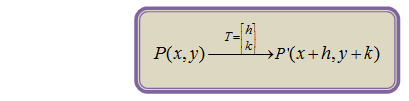
Titik P' disebut bayangan dari titik P.

Translasi dapat dilakukan secara berulang kali pada suatu titik. Translasi seperti ini disebut dengan komposisi translasi. Komposisi translasi dilakukan dengan menjumlahkan matriks translasinya terlebih dahulu. Kalian akan mempelajari lebih lanjut tantang komposisi translasi ini pada topik selanjutnya. Jangan sampai terlewat ya.

Dari penjelasan tersebut diatas dapat kita simpulkan beberapa sifat utama dari translasi, yaitu sebagai berikut.

• Translasi menggeser suatu titik dalam arah horizontal (sumbu-x) dan vertikal (sumbu-y).
• Pergeseran secara horizantal (sejajar sumbu-x) dituliskan dibaris pertama pada matriks translasi, sedangkan pergesaran secara vertikal (sejajar sumbu-y) dituliskan dibaris kedua pada matriks translasi.
• Pergeseran ke kanan dan ke atas bertanda positif (+) , sedangkan pergeseran ke kiri dan ke bawah bertanda negatif (-).
• Titik P(x,y) yang ditranslasi dengan sebarang matriks translasi T=[hk]$T=\left[\begin{array}{c}h\\ k\end{array}\right]$menghasilkan titik bayangan P’(x+h, y+k).
• Translasi tidak mengubah bentuk dan ukuran dari objek (figur) geometri yang ditranslasikan.

SOAL 1

Titik P(x,y) ditranslasikan oleh suatu matriks translasi ke titik P’(a,b). Matriks translasi yang dimaksud adalah….

SOAL 2

Segitiga ABC dengan koordinat titik sudut A(-1,0), B(3,0) dan C(0,4) memiliki luas 8 satuan. Apabila segitiga ini ditranslasi dengan matriks translasi T=[22]$T=\left[\begin{array}{c}2\\ 2\end{array}\right]$ maka luas dari segitiga hasil translasi adalah….

SOAL 3

Gambar yang menunjukan proses translasi pada segitiga ABC dengan benar adalah….

SOAL 4

Bayangan titik A(-3,7) setelah ditranslasi oleh matriks translasi T=[5−2]$T=\left[\begin{array}{c}5\\ -2\end{array}\right]$ adalah ...

SOAL 5

Matriks translasi T=[6−4]$T=\left[\begin{array}{c}6\\ -4\end{array}\right]$ menggeser titik Q ke titik Q’(10,2). Koordinat dari titik Q adalah….

SOAL 6

Suatu translasi memindahkan titik P(7,4) ke titik P’(2,8). Matriks translasi yang dimaksud adalah….

SOAL 7

Titik P(-2,5) ditranslasikan ke titik P’(-1,-2) dan kemudian dilanjutkan dengan sebuah translasi lain sehingga diperoleh bayangannya di titik P’’(2,2). Matrik translasi yang benar untuk menyatakan pergeseran titik P ke titik P’’ adalah….

SOAL 8

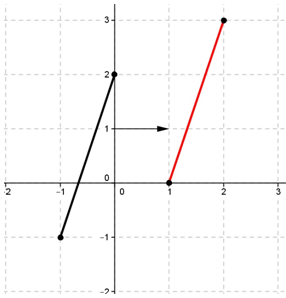
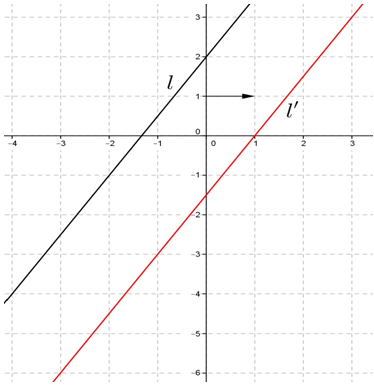
Perhatikan gambar translasi dari segmen garis berikut ini.

Matriks translasi yang tepat untuk menyatakan pergeseran segmen garis tersebut adalah….

SOAL 9

Bayangan dari titik P(3,6) yang ditranslasi secara berturut-turut oleh matriks T1=[2−1]$T_1=\left[\begin{array}{c}2\\ -1\end{array}\right]$ dan T2=[34]$T_2=\left[\begin{array}{c}3\\ 4\end{array}\right]$ adalah ....

SOAL 10

Perhatikan gambar translasi dari garis berikut ini.

Matriks translasi yang tidak menyatakan pergeseran garis l$l$ ke garis l′$l^{\prime }$ adalah….

Share this post