Contoh Soal Rumus Trigonometri Sudut Ganda

Contoh Soal Rumus Trigonometri Sudut Ganda - Kamu tentunya sudah tidak asing lagi dengan permainan komedi putar, bukan? Permainan ini menawarkan sensasi pemandangan kota dari ketinggian saat kamu berada di posisi tertentu pada lingkaran komedi putar. Namun, pernahkan terpikir olehmu berapa besar pertambahan tinggi yang dilewati dari suatu posisi ke posisi berikutnya? Berbeda dengan gerak lurus, pertambahan tinggi pada gerak melingkar dipengaruhi oleh besar sudut putar. Ini berarti, perpindahaan sebanyak dua kali suatu busur pada komedi putar, tidak serta merta membuatmu menempuh dua kali ketinggian semula.

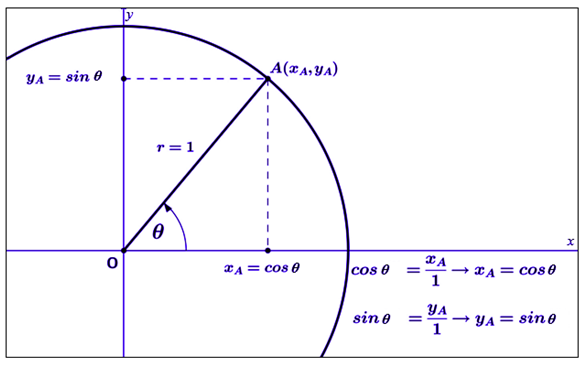
       Untuk menghitung ketinggian pada gerak melingkar, rumus-rumus trigonometri akan sangat berguna. Salah satunya adalah rumus trigonometri sudut ganda yang akan dibahas pada topik ini. Mari kita ingat kembali tentang identitas trigonometri cos2 x + sin2 x = 1 (identitas Pythagoras) terlebih dahulu. Identitas ini diperoleh dari hasil analisis lingkaran satuan dengan bantuan teorema Phytagoras. Perhatikan penjelasan berikut.

       Berdasarkan gambar di atas, identitas trigonometri cos2 x + sin2 x = 1 dapat dibuktikan dengan menerapkan teorema Pythagoras pada segitiga siku-siku AOXA. Tahukah kamu bahwa identitas ini juga dapat dibuktikan dengan memanfaatkan cos 0⁰ = 1? Mari simak penjabarannya berikut ini.

cos0∘=1⇔cos(x−x)=1⇔cosx.cosx+sinx.sinx=1⇔cos2x+sin2x=1$\begin{array}{l}\cos 0^{\circ }=1\\ \iff \cos (x-x)=1\\ \iff \cos x.\cos x+\sin x.\sin x=1\\ \iff {\cos }^{2}x+{\sin }^{2}x=1\end{array}$

       Pada topik sebelumnya, kamu telah mempelajari rumus trigonometri jumlah dan selisih dua sudut. Nah, melalui topik ini, kamu akan menemukan konsep rumus sudut ganda dengan memanfaatkan rumus trigonometri jumlah dua sudut dari sudut-sudut yang berukuran sama. Selain itu, kamu juga akan memanfaatkan prinsip yang digunakan untuk menunjukkan kebenaran identitas trigonometri cos2 x + sin2 x = 1 di atas.

Rumus Sinus Sudut Ganda

Mula-mula, gunakan rumus sinus jumlah dua sudut untuk menemukan rumus sinus sudut ganda.

sin(α+β)=sinαcosβ+cosαsinβ$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$

Misalkan α=β=x$\alpha =\beta =x$, sehingga diperoleh:

sin(α+β)=sinαcosβ+cosαsinβ⇔sin(x+x)=sinxcosx+cosxsinx⇔sin(x+x)=sinxcosx+sinxcosx⇔sin(x+x)=2sinxcosx$\begin{array}{l}\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\ \iff \sin (x+x)=\sin x\cos x+\cos x\sin x\\ \iff \sin (x+x)=\sin x\cos x+\sin x\cos x\\ \iff \sin (x+x)=2\sin x\cos x\end{array}$

Oleh karena sin (x + x) = sin 2x, maka rumus sinus sudut ganda dapat dinyatakan sebagai:

sin2x=2sinxcosx$\sin 2x=2\sin x\cos x$

Rumus Kosinus Sudut Ganda

Untuk menentukan rumus kosinus sudut ganda, gunakan cara yang sama dengan penentuan rumus sinus sudut ganda. Mula-mula, gunakan rumus kosinus jumlah dua sudut yaitu:

cos(α+β)=cosαcosβ−sinαsinβ$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

Misalkan α=β=x$\alpha =\beta =x$, sehingga diperoleh:

cos(α+β)=cosαcosβ−sinαsinβ⇔cos(x+x)=cosxcosx−sinxsinx⇔cos(x+x)=cos2x−sin2x$\begin{array}{l}\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\ \iff \cos (x+x)=\cos x\cos x-\sin x\sin x\\ \iff \cos (x+x)={\cos }^{2}x-{\sin }^{2}x\end{array}$

Oleh karena cos (x + x) = cos 2x, maka rumus kosinus sudut ganda dapat dinyatakan sebagai:

cos2x=cos2x−sin2x$\cos 2x={\cos }^{2}x-{\sin }^{2}x$

       Perhatikan bahwa terdapat kemiripan antara rumus kosinus sudut ganda dengan identitas trigonometri cos2 x + sin2 x = 1. Hal ini memungkinkan kita untuk memodifikasi rumus kosinus sudut ganda dengan langkah-langkah sebagai berikut.

• Mula-mula ubah identitas trigonometri cos2 x + sin2 x = 1 menjadi dua bentuk yaitu:

cos2 x + sin2 x =1 
⇔ cos2 x = 1 – sin2 x ... (1)
⇔ sin2 x = 1 – cos2 x ... (2)

• Selanjutnya, substitusi cos2 x = 1 – sin2 x ke rumus kosinus sudut ganda, sehingga:

cos2x=cos2x−sin2x⇔cos2x=(1−sin2x)−sin2x⇔cos2x=1−sin2x−sin2x⇔cos2x=1−2sin2x$\begin{array}{l}\cos 2x={\cos }^{2}x-{\sin }^{2}x\\ \iff \cos 2x=(1-{\sin }^{2}x)-{\sin }^{2}x\\ \iff \cos 2x=1-{\sin }^{2}x-{\sin }^{2}x\\ \iff \cos 2x=1-2{\sin }^{2}x\end{array}$

Dengan demikian, bentuk kedua dari rumus kosinus sudut ganda yaitu:

cos2x=1−2sin2x$\cos 2x=1-2{\sin }^{2}x$

• Substitusi sin2 x = 1 – cos2 x ke rumus kosinus sudut ganda, sehingga:

cos2x=cos2x−sin2x⇔cos2x=cos2x−(1−cos2x)⇔cos2x=cos2x−1+cos2x⇔cos2x=2cos2x−1$\begin{array}{l}\cos 2x={\cos }^{2}x-{\sin }^{2}x\\ \iff \cos 2x={\cos }^{2}x-(1-{\cos }^{2}x)\\ \iff \cos 2x={\cos }^{2}x-1+{\cos }^{2}x\\ \iff \cos 2x=2{\cos }^{2}x-1\end{array}$

Dengan demikian, bentuk ketiga dari rumus kosinus sudut ganda yaitu:

cos2x=2cos2x−1$\cos 2x=2{\cos }^{2}x-1$

Rumus Tangen Sudut Ganda

Untuk menentukan rumus tangen sudut ganda, gunakan langkah-langkah yang sama dengan penentuan rumus sudut ganda sebelumnya. Mula-mula, gunakan rumus tangen jumlah dua sudut yaitu:

tan(α+β)=tanα+tanβ1−tanαtanβ$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$

Misalkan α=β=x$\alpha =\beta =x$, sehingga diperoleh:

tan(α+β)=tanα+tanβ1−tanαtanβ$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$

⇔tan(x+x)=tanx+tanx1−tanxtanx$\iff \tan (x+x)=\frac{\tan x+\tan x}{1-\tan x\tan x}$

⇔tan(x+x)=2tanx1−tan2x$\iff \tan (x+x)=\frac{2\tan x}{1-{\tan }^{2}x}$

Oleh karena tan (x + x) = tan (2x), maka rumus tangen sudut ganda dapat dinyatakan sebagai:

tan2x=2tanx1−tan2x$\tan 2x=\frac{2\tan x}{1-{\tan }^{2}x}$

Modifikasi Lanjutan

Kita masih dapat memodifikasi lagi trigonometri sudut ganda dengan memanfaatkan prinsip bahwa setiap besar sudut dapat dibagi dua sama besar. Ini berarti, setiap besar sudut x dapat ditulis menjadi x=12x+12x$x=\frac{1}{2}x+\frac{1}{2}x$. Dengan menggunakan prinsip ini, diperoleh rumus trigonometri setengah sudut yaitu:

sin12x=1−cosx2−−−−−√$\sin \frac{1}{2}x=\sqrt{\frac{1-\cos x}{2}}$

cos12x=1+cosx2−−−−−√$\cos \frac{1}{2}x=\sqrt{\frac{1+\cos x}{2}}$

tan12x=1−cosx1+cosx−−−−−√dengancosx≠−1$\tan \frac{1}{2}x=\sqrt{\frac{1-\cos x}{1+\cos x}}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{n}\cos x\ne -1$

Pembuktian rumus trigonometri setengah sudut

• Untuk sin12x=1−cosx2−−−−−√$\sin \frac{1}{2}x=\sqrt{\frac{1-\cos x}{2}}$

Dengan memodifikasi rumus cos2x=1−2sin2x$\cos 2x=1-2{\sin }^{2}x$ menjadi cosx=1−2sin212x$\cos x=1-2{\sin }^2\frac{1}{2}x$, diperoleh:

cosx=1−2sin212x$\cos x=1-2{\sin }^2\frac{1}{2}x$

⇔2sin212x=1−cosx$\iff 2{\sin }^2\frac{1}{2}x=1-\cos x$

⇔sin212x=1−cosx2$\iff {\sin }^2\frac{1}{2}x=\frac{1-\cos x}{2}$

⇔sin12x=1−cosx2−−−−−√$\iff \sin \frac{1}{2}x=\sqrt{\frac{1-\cos x}{2}}$

• Untuk cos12x=1+cosx2−−−−−√$\cos \frac{1}{2}x=\sqrt{\frac{1+\cos x}{2}}$

Dengan memodifikasi rumus cos2x=2cos2x–1$\cos 2x=2{\cos }^{2}x–1$ menjadi cosx=2cos212x–1$\cos x=2{\cos }^2\frac{1}{2}x–1$, diperoleh:

cosx=2cos212x–1⇔2cos212x=1+cosx⇔cos212x=1+cosx2⇔cos12x=1+cosx2−−−−−√$\begin{array}{l}\cos x=2{\cos }^2\frac{1}{2}x–1\\ \iff 2{\cos }^2\frac{1}{2}x=1+\cos x\\ \iff {\cos }^2\frac{1}{2}x=\frac{1+\cos x}{2}\\ \iff \cos \frac{1}{2}x=\sqrt{\frac{1+\cos x}{2}}\end{array}$

• Untuk tan12x=1−cosx1+cosx−−−−−√,cosx≠−1

SOAL 1

Pernyataan berikut ini yang tepat tentang sin 2x adalah ….

SOAL 2

Pernyataan berikut yang tepat tentang kosinus sudut ganda adalah….

SOAL 3

Jika sin 27⁰ = 0,45, maka nilai dari sin 54⁰ adalah ….

SOAL 4

Jika sin 31⁰ = 0,52, maka nilai dari cos 62⁰ adalah ….

SOAL 5

Penjabaran rumus sudut ganda yang tepat dari cos 6x adalah….

SOAL 6

Diketahui sinx=35$\sin x=\frac{3}{5}$ dengan 0⁰ ≤ x ≤ 90⁰. Nilai dari sin 2x adalah ….

SOAL 7

Untuk nilai cosx=1213$\cos x=\frac{12}{13}$ dengan 0⁰ ≤ x ≤ 90⁰. Nilai cos 2x adalah ….

SOAL 8

Diketahui cosα=12dengan0≤α≤π2$\cos \alpha =\frac{1}{2}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{n}0\le \alpha \le \frac{\pi }{2}$, maka nilai dari sin12α$\sin \frac{1}{2}\alpha$ adalah….

SOAL 9

Jika cosα=13√$\cos \alpha =\frac{1}{\sqrt{3}}$ dengan α sudut lancip, maka nilai dari tan12α$\tan \frac{1}{2}\alpha$ adalah….

SOAL 10

Jika sinα=513$\sin \alpha =\frac{5}{13}$ dengan 90⁰ ≤ α ≤ 180⁰, maka nilai dari sin 2α adalah .…

Share this post