Contoh Soal Harga harapan dari suatu variabel random
Contoh Soal Harga harapan dari suatu variabel random - Kita telah mempelajari tentang variabel random (acak) dan penggunaannya. Meskipun demikian, bagaimana kita mencari mean dari variabel random yang merupakan bagian dari sebuah ruang sampel yang besar? Nilai harapan dari sebuah variabel random digunakan untuk menghitung mean dari variabel random.

Dalam pelajaran ini kita akan mempelajari cara untuk
- Menghitung nilai harapan dari variabel random; menjelaskannya sebagai mean dari distribusi peluang.
Nilai harapan dari variabel random adalah rata-rata tertimbang atau nilai tengah dari semua nilai yang mungkin dari variabel random. Simbol dari nilai harapan adalah E(x) dan rumus untuk variabel random diskret adalah
E(x) = x1P(1) + x2P(2) + ……… + xP(x)
Di mana variabel random X mengasumsikan nilai x1, x2…… x dengan peluang P(1), P(2)…. P(x)
E(x) = ∑ xP(x)
di mana x adalah jumlah dari nilai-nilainya, dihitung berdasarkan peluang yang bersangkutan.
Nilai harapan dalam jangka lama berarti bahwa jika nilai random dari sebuah eksperimen dikumpulkan terus-menerus, maka mean sampel atau rata-ratanya menjadi lebih dekat ke nilai harapan. Ada kemungkinan nilai harapan yang diperoleh itu mustahil atau tidak ada di kehidupan nyata. Nilainya bisa jadi 3.7 manusia atau 4.5 anak. Nilai harapan hanya bergantung pada data yang digunakan untuk menghitungnya.
Nilai harapan digunakan ketika menghimpun sekelompok besar angka, seperti pada saat sensus. Dalam sebuah sensus tidak dibutuhkan angka (data) tunggal, tetapi kita membutuhkan sebuah rata-rata atau mean.
Contohnya, ketika sebuah dadu dilemparkan, peluang munculnya angka 1, 2, 3, 4, 5, 6 adalah 1/6.

Contoh:
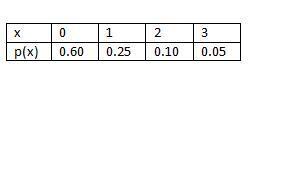
Seseorang mempunyai asuransi mobil dari sebuah perusahaan yang dipilih secara acak. Misalkan X adalah jumlah pelanggaran tertulis yang dilakukan oleh orang tersebut selama kurun waktu 3 tahun. Data X dapat ditulis dalam tabel seperti di bawah ini.

(a) Hitung E(X)
Penjelasan:
Soal yang diberikan adalah contoh dari variabel random diskret karena ada nilai yang terhingga dan berbeda (unik).
Berdasarkan rumus nilai harapan untuk variabel random diskret
E(x) = x1P(1) + x2P(2) + ……… + xP(x)
E(x) = 0 × 0.60 + 1 × 0.25 + 2 × 0.10 + 3 × 0.05
E(x) = 0 + 0.25 + 0.20 + 0.15
E(x) = 0.60
S1
Harga harapan dari suatu variabel random adalah _____________ dari semua kemungkinan hasilnya.
S2
Berapakah harga harapan dari sebuah dadu standar?
S3
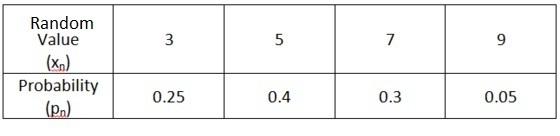
Tentukan harga harapan dari kejadian yang diberikan oleh data berikut:

S4
Probabilitas memperoleh angka pada sebuah dadu tak seimbang adalah {(1,0.3), (2,0.05), (3,0.1), (4,0.1), (5,0.2), (6,0.25)}. Berapakah harga harapan untuk dadu ini?
S5
Sebuah dadu tak seimbang sedemikian hingga probabilitas mendapatkan angka enam tiga kali lebih besar daripada angka-angka yang lain. Berapakah harga harapan ketika dadu dilempar?
S6
Biaya pembuatan karangan bunga adalah $1. Karangan bunga dijual seharga $5 jika bunga-bunganya segar. Harga karangan bunga turun ke $3 pada hari kedua sedangkan pada hari ketiga turun ke $1, dan setelah itu dibuang. Jika probabilitas karangan bunga terjual pada hari pertama adalah 0,4, pada hari kedua 0,25 dan pada hari ketiga 0,1, berapakah harapan keuntungan per harinya (dibulatkan ke satuan dollar terdekat) jika rata-rata 120 karangan bunga dijual dalam seminggu?
S7
Sebuah dadu non-standar dinomori {4,4,4,4,6,7}. Probabilitas munculnya masing-masing angka adalah {0,08, 0,12, 0,24, 0,18, 0,21, 0,17}. Berapakah harga harapan jika dadu ini dilempar?
S8
Sebuah toko roti terkenal akan kue-kuenya. Harga kue tersebut $10. Jika seorang pelanggan membeli dua kue, ia akan mendapat diskon 10%. JIka ia membeli tiga kue, maka ia mendapat diskon 20%. Jika ia membeli empat kue atau lebih ia mendapat diskon 25%. Rata-rata, 50% pelanggan membeli satu kue, 20% membeli dua kue, 15% membeli tiga kue dan 10% membeli empat kue dan sisanya memesan dalam jumlah besar yaitu lima kue. Rata-rata biaya pembuatan satu kue adalah $6,50. JIka toko roti itu menjual 100 kue per minggu, berapakah rata-rata keuntungan harian dari toko roti itu?
S9
Dalam sebuah permainan peluang, dua dadu dilempar secara bersamaan. Pemain harus menebak sebelum melempar dadu apakah hasil lemparannya kurang dari 7, sama dengan 7 atau lebih dari 7. Jika tebakannya salah, maka uangnya hilang seluruhnya, sedangkan jika tebakannya tepat, maka sang pemain mendapat hadiah yang sesuai. Pada sebuah pasar malam, uang yang dipertaruhkan adalah $10. Jika permainannya adil, maka berapakah hadiah yang sesuai untuk berhasil menebak salah satu dari (kurang dari 7, sama dengan 7, lebih dari 7)?
Sebuah permainan dikatakan adil jika harga harapan hadiahnya sama dengan uang yang beresiko hilang.
S10
Dua dadu non-standar dilempar bersamaan. Satu dadu dinomori {4,4,8,8,8,12}, dadu yang lain dinomori {3,5,5,8,8,11}. Dadu pertama tidak seimbang sedemikian hingga sisi bernomor 12 memiliki probabilitas muncul tiga kali lebih besar dari munculnya 4 dan dua sisi bernomor 8 memiliki probabilitas muncul dua kali munculnya 4. Sisi ketiga yang bernomor 8 memiliki probabilitas yang sama dengan sisi bernomor 4. Dadu kedua sangat tidak seimbang sedemikian hingga probabilitas dari sisi-sisi {3,5,5,8,8,11} berturut-turut adalah {0,1, 0,03, 0,2, 0,17, 0,32, 0,18}. Dua dadu ini dilempar bersamaan. berapakah harga harapan dari jumlahan angka yang muncul?
