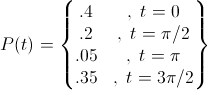Contoh Soal Grafik distribusi probabilitas
Contoh Soal Grafik distribusi probabilitas - Pada sesi kali ini kita akan belajar bagaimana membuat grafik dan belajar tentang grafik fungsi massa peluang (pmf) juga yang juga dikenal sebagai fungsi kepadatan probabilitas (pdf).
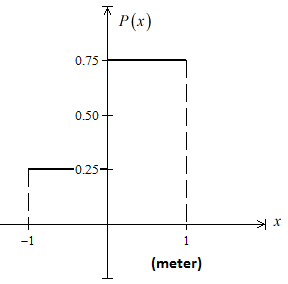
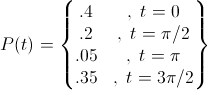
Pertama, terdapat pasangan aturan untuk fungsi massa peluang.
1. Semua peluang pasti diantara 0 dan 1.
2. Jumlah total semua peluang sama dengan 1.
Contoh 1: Apakah berikut ini merupakan grafik fungsi massa peluang?
Tidak, grafik tersebut bukan merupakan fungsi massa peluang karena tidak memenuhi kedua syarat yang ada. Pertama, peluang mendapatkan 3 adalah 4 bukan nilai antara 0 sampai 1. Kedua, jumlah semua peluangnya adalah 8 bukan 1.
Selanjutnya, diberikan himpunan kejadian atau bilangan, kita akan mencari cara untuk membentuk sebuah fungsi massa peluang.
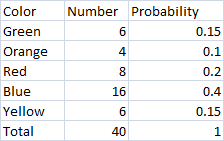
Contoh 2: Sebuah tas berisi 6 kelereng hijau, 4 kelereng oranye, 8 kelereng merah, 16 kelereng birum dan 6 kelereng kuning. Bentuklah sebuah distribusi fungsi massa peluang.
Pertama, kita akan menentukan peluang dari setiap hasil dengan membentuk tabel. Untuk menentukan peluang kita perlu mengambil banyaknya kajadian yang dicari dibagi jumlah semua kejadian. Sebagai contoh, untuk kelereng hijau, kita mempunyai 6 kelereng hijau dan jumlah semua kelereng adalah 6+4+8+16+6=40 kelereng. Sehingga peluang kelereng hijau adalah 6/40=.15
Kita dapat melihat bahwa ternyata ini merupakan fungsi massa peluang karena semua peluang terletak diantara 0 dan 1 dan jumlah semua peluang adalah 1.
Akhirnya, kita dapat menggunakan peluang di atas untuk mencari distribusi.
Membaca peluang dari bagan ini sangat mudah. Sebagai contoh, jika kita mencari pepluang dari kelereng merah atau biru maka kita hanya perlu menghitung 2+.4=.6.
S1
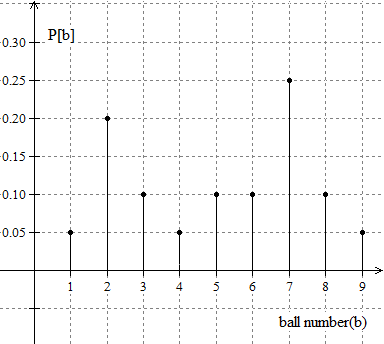
Anda diberi sebuah tas yang berisi bola-bola ping pong yang identik. Setiap bola bertuliskan angka dari himpunan berikut : { 1, 2, 3, 4, 5, 6, 7, 8, 9}. Banyaknya bola yang dinomori angka tertentu bervariasi sehingga fungsi massa probabilitas untuk pengambilan satu bola dari dalam tas tanpa melihat digambarkan di grafik di bawah ini. Berapakah probabilitas P[ b = prime], i.e. probabilitas bola yang diambil dari dalam tas bertuliskan bilangan prima?
S2
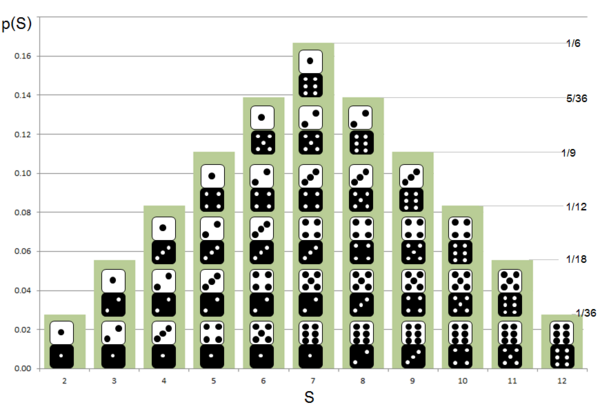
Di bawah ini adalah fungsi massa probabilitas untuk kejadian yang didefinisikan oleh jumlahan hasil lemparan 2 dadu. Berapakah probabilitas hasil jumlahannya, S, sama dengan kuadrat sempurna, i.e. P[S = kuadrat sempurna]?
S3
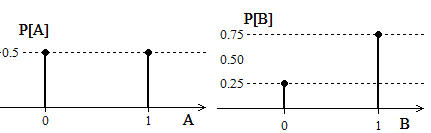
Diberikan dua fungsi massa probabilitas diskrit dari dua variabel random, A dan B, yang independen, seperti di bawah ini. Manakah dari grafik-grafik berikut yang merupakan distribusi probabilitas bersama dari A dan B, i.e P(A = a, B = b)?
S4
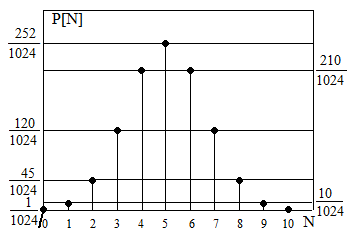
Sebuah uang logam yang terdiri atas dua sisi (ekor dan kepala) diundi sebanyak sepuluh kali. Diketahui bahwa variabel random N menyatakan banyak munculnya bagian kepala dari hasil pengundian.
Fungsi densitas probabilitas dari percobaan di atas adalah sebagai berikut.
Probabilitas kejadian munculnya bagian ekor sebanyak bilangan prima adalah ….
S5
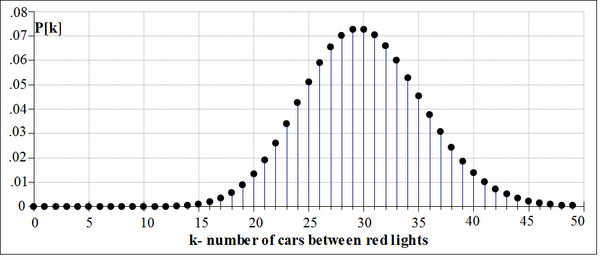
Di sebuah persimpangan lampu merah, probabilitas banyaknya mobil, namakan k, yang berhenti di lampu lalu lintas saat menyala warna merah selama jam sibuk didefinisikan oleh fungsi massa probabilitas, P(k), seprti di bawah ini. Grafik fungsi dilukis untuk k = 0 mobil sampai k = 50 mobil. Untuk nilai k berapakah P(k) > =0,05?
S6
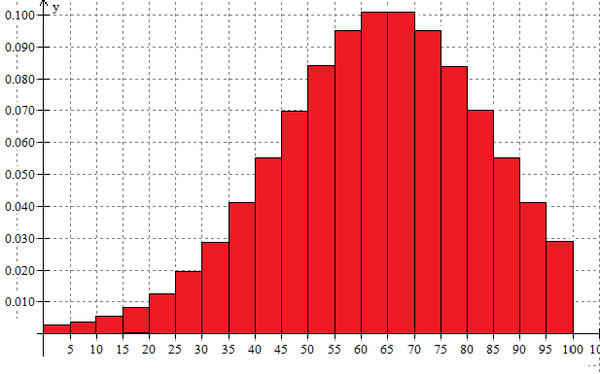
Di bawah ini adalah distribusi dari skor tes terstandarisasi yang direpresentasikan dalam histogram. Sisi vertikal persegi panjang merepresentasikan probabilitas siswa akan mendapat nilai diantara interval yang bersesuaian, i.e. P[ 60 < x < 65 ] ≈ 0.1. Skor berdistribusi normal dengan rata-rata 70 dan deviasi standar 20. Manakah diantara ini yang memberikan estimasi terbaik untuk probabilitas nilai seorang siswa di atas 80?
S7
Seseorang yang sedang mabuk berat sedang dalam perjalanan pulang dari sebuah pesta. Ia telah berupaya sekuat tenaga untuk dapat sampai di halaman depan rumahnya. Nah, saat ini ia harus melakukan langkah terakhir untuk menuju pintu rumahnya yang terletak pada sumbu X positif dari lokasi ia berada.
Pada sebarang langkah yang diberikan, jarak yang ditempuh sepanjang sumbu X oleh orang tersebut dideskripsikan dengan fungsi densitas probabilitas berikut.
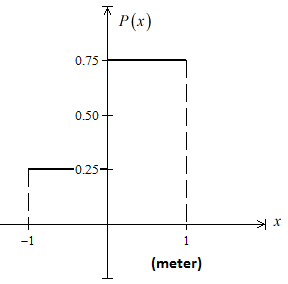
Probabilitas bahwa panjang dari masing-masing langkah yang diberikan terletak dalam interval [0 , 1] , [-1 , 0] ,
dan [0,5 , 1] berturut-turut adalah ….
dan [0,5 , 1] berturut-turut adalah ….
S8
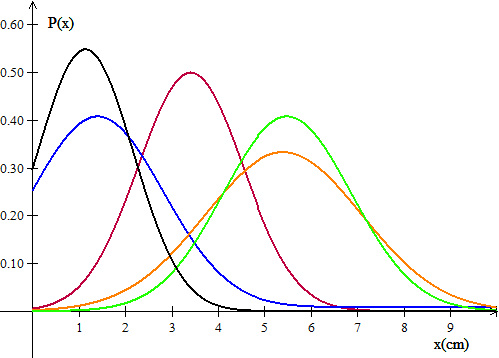
Anda sedang bermain dart melawan DartBot, sebuah robot yang didesain untuk bermain dart. Robot itu memiliki 5 pengaturan kesulitan yang dapat anda pilih untuk dilawan. Masing-masing pengaturan ini berkorespondensi dengan sebuah distribusi probabilitas yang mendefinisikan probabilitas robot itu akan melempar sebuah dart dari jarak tertentu tepat sasaran. Distribusi probabilitas dari masing-masing pengaturan ditunjukkan di bawah ini. Distribusi warna manakah yang merepresentasikan pengaturan yang tersulit dan yang termudah?
S9
Berikut ini adalah sejumlah grafik fungsi massa probabilitas dari beberapa distribusi binomial. Banyaknya rangakaian percobaan adalah 4. Manakah dari grafik berikut yang merepresentasikan eksperimen yang probabilitas suksesnya paling besar?
S10
Sebuah gelombang spasial sinus satu dimensi didefinisikan oleh persamaan berikut: V(x) = cos(kx + t) . Fase dari gelombang ini merupakan variabel random, t, yang mengambil 4 kemungkinan nilai diskrit dengan 4 probabilitas berbeda yang didefinisikan di bawa ini. Manakah fungsi massa probabilitas berikut yang berkorespondensi dengan fase random diskrit, t?