Konsep Barisan Tak Hingga
Konsep Barisan Tak Hingga - Pada topik ini kita akan belajar barisan dan deret, terbagi menjadi barisan bilangan, deret bilangan, barisan aritmetika, deret aritmetika, barisan geometri, deret geometri, dan deret geometri tak hingga. Mari satu per satu kita pelajari.












 |
| Konsep Barisan Tak Hingga |
Barisan bilangan
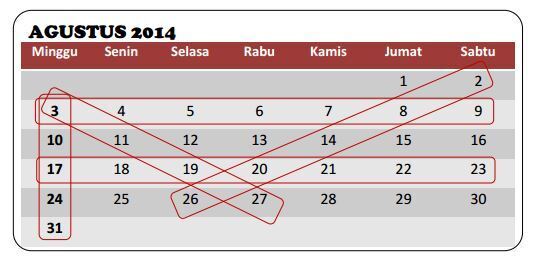
Mari kita perhatikan gambar kalender berikut:
Mari kita perhatikan gambar kalender berikut:

Dari kalender di atas kalian dapat mengambil sekumpulan bilangan dalam urutan baris, kolom, atau diagonal, misalnya
1) 3, 4, 5, 6, 7, 8, 9
2) 17, 18, 19, 20, 21, 22, 23
3) 3, 10, 17, 24, 31
4) 3, 11, 19, 27
5) 26, 20, 14, 8, 2
1) 3, 4, 5, 6, 7, 8, 9
2) 17, 18, 19, 20, 21, 22, 23
3) 3, 10, 17, 24, 31
4) 3, 11, 19, 27
5) 26, 20, 14, 8, 2
Kalian perhatikan, bahwa masing-masing kumpulan bilangan tersebut memiliki pola tertentu.
1) Suku berikutnya didapat dari suku sebelumnya ditambah 1
2) Suku berikutnya didapat dari suku sebelumnya ditambah 1
3) Suku berikutnya didapat dari suku sebelumnya ditambah 7
4) Suku berikutnya didapat dari suku sebelumnya ditambah 8
5) Suku berikutnya didapat dari suku sebelumnya dikurangi 6
Kumpulan bilangan tersebut disebut barisan bilangan.
1) Suku berikutnya didapat dari suku sebelumnya ditambah 1
2) Suku berikutnya didapat dari suku sebelumnya ditambah 1
3) Suku berikutnya didapat dari suku sebelumnya ditambah 7
4) Suku berikutnya didapat dari suku sebelumnya ditambah 8
5) Suku berikutnya didapat dari suku sebelumnya dikurangi 6
Kumpulan bilangan tersebut disebut barisan bilangan.
Jadi, dapat kita katakan bahwa barisan bilangan adalah susunan bilangan yang memiliki aturan tertentu dan dipisahkan oleh tanda koma.
Bilangan pertama disebut suku pertama (U1) , bilangan kedua disebut suku kedua (U2) , dan seterusnya bilangan ke-n
disebut suku ke-n (Un) .
Bilangan pertama disebut suku pertama (U1) , bilangan kedua disebut suku kedua (U2) , dan seterusnya bilangan ke-n
disebut suku ke-n (Un) .
Untuk lebih jelasnya, perhatikan contoh berikut ini!




Deret bilangan
Sebelumnya kalian telah belajar tentang barisan bilangan, yang secara umum ditulis:
U1, U2, U3,...,Un
U1, U2, U3,...,Un
Jika tanda koma kita ganti dengan tanda penjumlahan (+), kita peroleh deret bilangan, yang ditulis:
U1 + U2 + U3 +...+ Un
U1 + U2 + U3 +...+ Un
Pada deret bilangan, selain kita bicara suku ke- n kita juga bicara tentang jumlah deret tersebut.
Untuk lebih jelasnya, perhatikan contoh berikut!
Contoh:
Hitunglah jumlah deret 3 + 7 + 11 +...+ 79
Hitunglah jumlah deret 3 + 7 + 11 +...+ 79
Pembahasan:
Kita lihat lebih dulu pola deret tersebut.
U1 = 3 = 4(1) - 1
U2 = 7 = 4(2) - 1
U3 = 11 = 4(3) - 1
dan seterusnya sampai suku ke- n diperoleh pola Un = 4n - 1
Kita lihat lebih dulu pola deret tersebut.
U1 = 3 = 4(1) - 1
U2 = 7 = 4(2) - 1
U3 = 11 = 4(3) - 1
dan seterusnya sampai suku ke- n diperoleh pola Un = 4n - 1
Selanjutnya kita cara banyaknya suku dengan memandang 79 adalah suku ke- n
Un = 79 maka 4n - 1 = 79 => n = 20 , berarti banyak suku ada 20 .
Un = 79 maka 4n - 1 = 79 => n = 20 , berarti banyak suku ada 20 .
Untuk mencari jumlahnya kita ambil pasangan dua suku seperti berikut :
U1 + U20 = 3 + 79 = 82
U2 + U19 = 7 + 75 = 82
U3 + U18 = 11 + 71 = 82
U2 + U19 = 7 + 75 = 82
U3 + U18 = 11 + 71 = 82
dan seterusnya sampai 10 pasang maka jumlah deret = 82 x 10 = 820

Contoh:
Diberikan barisan aritmetika 1,4,7,... . Tentukan suku ke- 250
Diberikan barisan aritmetika 1,4,7,... . Tentukan suku ke- 250
Pembahasan:
Diketahui a = 1, b = 3
Un = a + (n - 1)b maka U250 = 1 + (250 - 1)(3) = 748
Jadi suku ke- 250 = 748
Diketahui a = 1, b = 3
Un = a + (n - 1)b maka U250 = 1 + (250 - 1)(3) = 748
Jadi suku ke- 250 = 748






