Contoh Soal Menggambar Grafik Fungsi Linear

Contoh Soal Menggambar Grafik Fungsi Linear - Mari simak ilustrasi berikut.

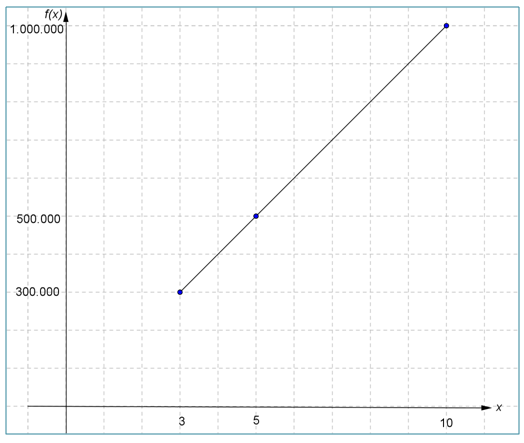
Banyaknya tabungan Tegar dapat dinyatakan dalam sebuah fungsi yaitu f(x) = 100.000x dengan f (x) adalah besar tabungan dan x adalah lama waktu menabung (dalam bulan). Jika kita ingin mengetahui besar tabungan Tegar pada bulan ke-3, ke-5, dan ke-10, maka kita dapat mensubstitusikan x = 3, x = 5, dan x = 10 ke rumus fungsi f (x) yaitu:

f (3) = 100.000 × 3 = 300.000
f (5) = 100.000 × 3 = 500.000
f (10) = 100.000 × 3 = 1.000.000

Ini berarti, besar tabungan Tegar pada bulan ke-3, ke -5, dan ke-10 yaitu Rp300.000,00, Rp500.000,00, dan Rp1.000.000,00. Nilai fungsi tabungan Tegar pada bulan ketiga, kelima, dan kesepuluh dapat dinyatakan dalam suatu sistem koordinat Cartesiussebagai berikut.

Perhatikan kembali ilustrasi di atas. Fungsi f (x) yang menyatakan banyaknya tabungan Tegar merupakan salah satu contoh fungsi linear. Agar kamu lebih paham tentang menggambar grafik fungsi linear, mari kita ingat kembali tentang menghitung nilai fungsi dan tabel fungsi.

Menghitung Nilai Fungsi

Jika diketahui rumus fungsi f (x), maka nilai fungsi dapat ditentukan dengan cara mensubstitusikan nilai x pada rumus fungsi tersebut.

✎Contoh 1

Diketahui f (x) = 5x + 7. Tentukan nilai fungsi tersebut untuk x = 2.

Penyelesaian:

f (2) = 5(2) + 7 = 10 + 7 = 17

Jadi, nilai fungsi f (x) = 5x + 7 untuk x = 2 adalah 12.

Tabel Fungsi

Tabel fungsi memuat anggota-anggota daerah asal (domain) dan bayangannya (range). Pada tabel fungsi dapat dilihat nilai variabel bebas yang berubah sesuai dengan fungsinya.

✎Contoh 2

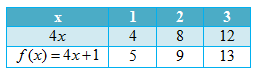
Fungsi f (x) = 4x + 1 dengan daerah asal {1, 2, 3}. Tentukan nilai fungsi tersebut dengan menggunakan tabel fungsi.

Penyelesaian:

Tabel fungsi f adalah:

Dari tabel di atas diperoleh:
untuk x = 1 → f (1) = 4(1) + 1 = 5
untuk x = 2 → f (2) = 4(2) + 1 = 9
untuk x = 3 → f (3) = 4(3) + 1 = 13

Jadi, nilai fungsi f (x) = 4x + 1 dengan daerah asal {1, 2, 3} adalah {5, 9, 13}.

Dari nilai fungsi f (x) = 4x + 1 diperoleh bahwa jika nilai x bertambah dari x = 1 ke x = 2, maka nilai f (x) juga bertambah sebanyak 4 yaitu dari 5 ke 9.

Menggambar Grafik Fungsi Linear

Fungsi linear adalah suatu fungsi yang variabelnya berpangkat satu dengan grafik berupa garis lurus. Bentuk umum fungsi linear yaitu:

f : x → ax + b atau f (x) = ax + b atau y = ax + b

dengan:

• variabel x disebut variabel bebas.
• variabel y atau f (x) disebut variabel terikat.

Suatu fungsi dari himpunan A ke himpunan B dapat dinyatakan dengan grafik fungsi. Grafik fungsi adalah penyajian fungsi ke dalam bentuk diagram Cartesius.

Cara Menggambar Grafik Fungsi Linear

Cara I
Langkah-langkah menggambar grafik fungsi linear dengan cara I adalah sebagai berikut.

✔ Tentukan pasangan-pasangan berurutan (x, y) dengan x adalah anggota domain dan y adalah bayangan dari x (range) dengan menggunakan tabel fungsi.

✔ Buatlah sumbu mendatar dan sumbu tegak yang saling berpotongan dengan:

• anggota domain berada pada sumbu mendatar atau sumbu x.
• anggota range berada pada sumbu tegak atau sumbu y.

✔ Tentukan letak pasangan berurutan (x, y) pada bidang koordinat yang ditandai dengan titik atau noktah.

✔ Hubungkan titik-titik tersebut dengan sebuah garis lurus.

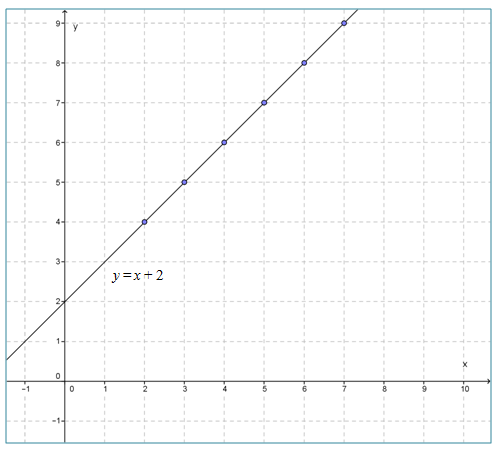
✎Contoh 3

Gambarkan grafik fungsi y = x + 2 dengan x adalah bilangan bulat positif antara 1 dan 8.

Penyelesaian:

Diketahui:
fungsi y = x + 2
x adalah bilangan bulat positif antara 1 dan 8

Ini berarti, x = {2, 3, 4, 5, 6, 7}.

Tabel fungsi y = x + 2 adalah:

Grafik fungsinya adalah sebagai berikut.

Cara II
Langkah-langkah menggambar grafik fungsi linear dengan cara II adalah sebagai berikut.

✔Tentukan titik potong terhadap sumbu x dengan syarat y = 0, sehingga diperoleh koordinat A (x1, 0).

✔Tentukan titik potong terhadap sumbu y dengan syarat x = 0, sehingga diperoleh koordinat B (0, y1).

✔Hubungkan titik A dan B sehingga membentuk suatu garis lurus.

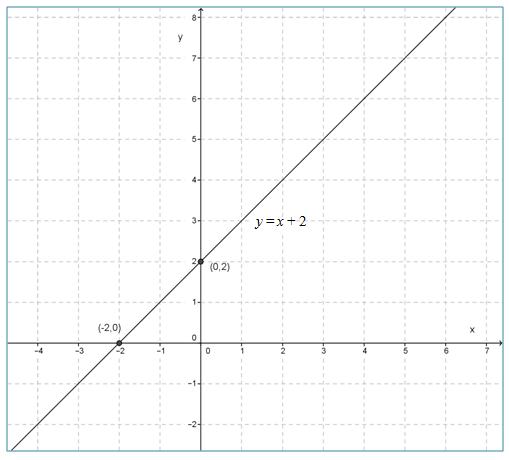
✎Contoh 4

Gambarkan grafik fungsi y = x + 2.

Penyelesaian:

Diketahui fungsi y = x + 2.

Titik potong sumbu x (y = 0)
y = x + 2 
⇔ 0 = x + 2
⇔ x = 0 – 2 
⇔ x = -2
∴ Titik potong sumbu x adalah (-2, 0).

Titik potong sumbu y (x = 0)
y = x + 2 
⇔ y = 0 + 2
⇔ y = 2
∴ Titik sumbu y adalah (0, 2).

Grafik fungsi y = x + 2 adalah sebagai berikut.

Catatan:

• untuk menggambar grafik fungsi linear dibutuhkan minimal 2 titik.
• untuk menggambar grafik fungsi linear, kamu bebas memilih cara I atau cara II karena apapun cara yang digunakan, hasilnya akan sama.

S1

Pilihan Tunggal

Grafik yang menunjukkan grafik fungsi linear adalah ....

S2

Pilihan Tunggal

Diketahui grafik fungsi sebagai berikut.

Berdasarkan grafik fungsi di atas, jika y = {1, 3, 5}, maka x = ....

S3

Pilihan Tunggal

Diketahui gambar berikut.

Berdasarkan grafik fungsi di atas, jika {x | 0 < x ≤ 3, x ϵ bilangan bulat}, maka salah satu nilai y = ....

S4

Pilihan Tunggal

Grafik fungsi y = x - 2 adalah ....

S5

Pilihan Tunggal

Diketahui y = 2x - 3. Grafik fungsi linearnya adalah ....

S6

Pilihan Tunggal

Diketahui y = 4x - 2. Grafik fungsi linearnya adalah ....

S7

Pilihan Tunggal

Grafik fungsi y = x - 5 adalah ....

S8

Pilihan Tunggal

Diketahui pernyataan-pernyataan berikut.

(1) Jika x = 0, maka y = -10
(2) Jika x = 0, maka y = 10
(3) Grafik fungsi:

(4) Grafik fungsi:

Pernyataan yang benar tentang fungsi y = 5x + 10 adalah ...

S9

Pilihan Tunggal

Diketahui pernyataan-pernyataan berikut.

(1) Jika y = 0, maka x = 2,5
(2) Jika y = 0, maka x = -2,5
(3) Grafik fungsi:

(4) Grafik fungsi:

Pernyataan yang benar tentang fungsi y = 2x - 5 adalah ....

S10

Pilihan Tunggal

Diketahui pernyataan-pernyataan berikut.

(1) Jika x = 0, maka y = -2
(2) Jika y = 0, maka x = 1
(3) Grafik fungsi:

(4) Grafik fungsi:

Jika fungsinya adalah y = 2x - 2, maka pernyataan yang benar adalah ....

Share this post