Contoh Soal Mengenal dan Melanjutkan Pola Bilangan

Contoh Soal Mengenal dan Melanjutkan Pola Bilangan - Suatu ketika, Dito pergi mendatangi rumah Bono untuk menanyakan sesuatu.

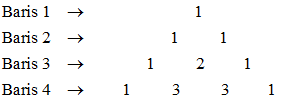
Rupanya ia masih merasa bingung dengan materi pola bilangan yang tadi siang dibahas 
di sekolah.

“Bon….sebenarnya yang dimaksud dengan pola itu apa sih?” tanya Dito pada Bono yang sedang asyik bermain gitar.
“Pola seringkali diartikan sebagai suatu struktur atau suatu susunan. Nah, berdasarkan arti tersebut, pola bilangan dapat diartikan sebagai suatu aturan dalam penyusunan bilangan atau struktur penyusunan bilangan.” jawab Bono.
“Lalu apa yang kita dapat dari susunan bilangan itu?” Dito semakin penasaran.
“Susunan bilangan yang teratur dan membentuk suatu pola tertentu nantinya akan membentuk suatu barisan bilangan.” jelas Bono.
“Contoh konkritnya bagaimana, Bon?” Dito masih tampak kebingungan.
“Coba amati gambar ini, Dit.” kata Bono sambil menunjukkan gambar berikut ini.

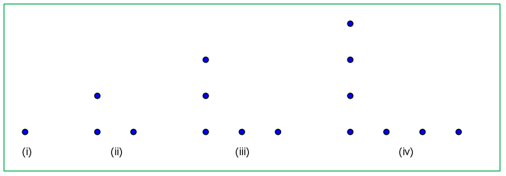
“Apakah menurutmu gambar di atas membentuk suatu pola?” tanya Bono pada Dito.
“Ya…tentu saja.” jawab Dito.
“Berapa banyak lingkaran pada tiap gambar tersebut?” tanya Bono sembari mengajak Dito mengamati gambar.
“1, 3, 5, dan 7… Wah, ternyata banyaknya lingkaran pada suku selanjutnya berasal dari banyaknya lingkaran pada suku sebelumnya ditambah dua lingkaran.” Dito tampak senang karena menemukan sesuatu.
“Nah, tanpa menggambar, dapatkah kamu menentukan banyaknya lingkaran pada tiga suku berikutnya?” Bono mulai memancing Dito untuk berpikir lebih keras.
“Tentu saja bisa. Banyaknya lingkaran pada tiga suku berikutnya adalah 9, 11, dan 13.” jawab Dito penuh semangat.
“Urutan bilangan 1, 3, 5, 7, 9, 11, 13, …. yang baru saja kita temukan itu disebut sebagai barisan bilangan.” urai Bono yang disambut anggukan oleh Dito.

POLA BILANGAN

Pola Bilangan Ganjil dan Pola Bilangan Genap

Jika kalian perhatikan, barisan bilangan 1, 3, 5, 7, 9, 11, 13, … yang dikemukakan oleh Bono dan Dito pada percakapan di atas ternyata tersusun atas bilangan ganjil. Nah, pola bilangan tersebut selanjutnya disebut dengan pola bilangan ganjil. Selanjutnya, pola pada barisan bilangan 2, 4, 6, 8, 10, … disebut dengan pola bilangan genap karena bilangan penyusunnya adalah bilangan genap.

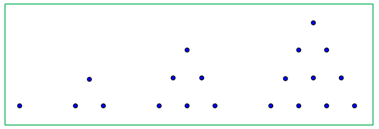
Pola Bilangan Segitiga

Pola bilangan segitiga ditentukan berdasarkan banyaknya lingkaran yang menyusun 
segitiga-segitiga pada gambar berikut.

Dengan demikian, barisan bilangan segitiga adalah 1, 3, 6, 10 , ….

Pola Bilangan Segitiga Pascal

Pola bilangan segitiga Pascal adalah sebagai berikut:

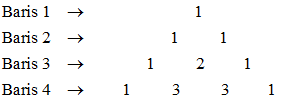
Pola Bilangan Fibonacci

Bilangan pertama dan kedua dari barisan bilangan Fibonacci adalah satu. Adapun bilangan ketiga dan selanjutnya diperoleh dengan cara menjumlahkan dua bilangan sebelumnya.

Barisan bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, ….

MELANJUTKAN POLA BILANGAN

Bagaimana cara melanjutkan pola bilangan?
Tentu saja kalian perlu mengetahui aturan atau cara yang digunakan untuk menyusun bilangan tersebut.

Ada suatu barisan bilangan yang mana setiap bilangannya diperoleh dengan cara menjumlahkan atau mengurangkan bilangan sebelumnya dengan suatu bilangan. 
Nah, barisan bilangan tersebut selanjutnya dikatakan menggunakan pola penjumlahan atau pola pengurangan.

Contoh 1:

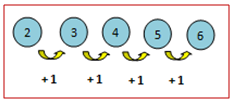
Bagaimanakah pola dari barisan bilangan 2, 3, 4, 5, 6, …?
Tentukan tiga bilangan selanjutnya.

Penyelesaian:

Pola dari barisan bilangan di atas diilustrasikan dalam gambar di bawah ini.

Pada gambar di atas, tampak bahwa bilangan kedua dan seterusnya diperoleh dengan cara menambahkan bilangan sebelumnya dengan bilangan satu. Dengan demikian, tiga bilangan selanjutnya adalah 7, 8, dan 9.

Contoh 2:

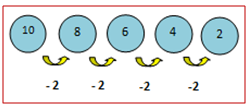
Lengkapilah titik-titik pada barisan bilangan 10, 8, 6, 4, 2, …, …, ….

Penyelesaian:

Pola bilangan pada barisan bilangan di atas diilustrasikan oleh gambar berikut.

Pada gambar di atas, tampak bahwa bilangan kedua dan selanjutnya diperoleh dengan cara mengurangkan suku sebelumnya dengan bilangan dua. Dengan demikian, tiga bilangan selanjutnya pada barisan tersebut adalah 0, -2, dan -4.

Perlu kalian ketahui, suatu barisan bilangan juga dapat diperoleh dengan mengikuti pola perkalian, pembagian, maupun perpangkatan. Mari kita perhatikan contoh berikut.

Contoh 3:

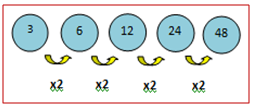
Bagaimanakah pola dari barisan bilangan 3, 6, 12, 24, 48, …?
Tentukan tiga bilangan selanjutnya.

Penyelesaian:

Pola dari barisan bilangan di atas diilustrasikan dalam gambar berikut.

Pada gambar di atas, tampak bahwa bilangan kedua dan seterusnya diperoleh dengan cara mengalikan bilangan sebelumnya dengan bilangan dua. Dengan demikian, tiga bilangan berikutnya adalah 96, 192, dan 384.

Contoh 4:

Tentukan nilai x pada barisan bilangan 1, 4, 9, x, 25.

Penyelesaian:

Jika kita perhatikan, bilangan di atas merupakan hasil dari perpangkatan kuadrat terhadap bilangan asli, yaitu

• 12 = 1
• 22 = 4
• 32 = 9

Oleh karena x pada barisan bilangan di atas merupakan bilangan ke-4, maka x = 42 = 16.

S1

Pilihan Tunggal

Pola dari barisan bilangan 3, 4, 7, 11, 18, … adalah ….

S2

Pilihan Tunggal

Tiga suku selanjutnya dari barisan bilangan 2, 3, 5, 7, … adalah ….

S3

Pilihan Tunggal

Nilai x, y, dan z pada barisan bilangan 2, 4, 8, 16, x, y, z berturut-turut adalah ….

S4

Pilihan Tunggal

Tiga bilangan selanjutnya dari barisan bilangan 
2, 6, 10, 14, 18, … adalah ….

S5

Pilihan Tunggal

Tiga bilangan selanjutnya dari barisan bilangan 
1, 8, 27, 64, … adalah ….

S6

Pilihan Tunggal

Tiga bilangan selanjutnya dari barisan bilangan 
60, 53, 46, 39, …. adalah ….

S7

Pilihan Tunggal

Dua bilangan selanjutnya dari barisan 
-2, 8, -32, 128, -512, … adalah ….

S8

Pilihan Tunggal

Barisan bilangan di baris ke-5 pada pola bilangan segitiga Pascal adalah ….

S9

Pilihan Tunggal

Jika pola pada barisan bilangan x, y, 11, 17, 26, 43, … merupakan pola bilangan Fibonacci, maka nilai x adalah ….

S10

Pilihan Tunggal

Jika pola pada barisan bilangan 10, x, y, 34, 56, 90 … merupakan pola bilangan Fibonacci, maka nilai (x.y) adalah ….

Share this post