Contoh Soal Volume Tabung
Contoh Soal Volume Tabung - Pada topik sebelumnya, kalian telah belajar tentang unsur tabung. Tabung dibentuk dari dua buah lingkaran yang menjadi alas dan tutupnya, serta selimut yang menjadi sisi tegaknya. Dua buah lingkaran yang saling berhadapan tersebut memiliki bentuk dan ukuran yang sama (kongruen).

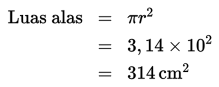

Coba perhatikan gambar di bawah ini.

Masih ingatkah kalian cara mencari volume prisma? Ya, benar sekali. Untuk mencari volume prisma, kita bisa gunakan rumus:
volume prisma = luas alas × tinggi
Kalau kita amati dengan baik, bentuk prisma dan tabung memiliki susunan yang mirip. Tabung merupakan sebuah prisma yang alasnya berupa lingkaran. Masih ingatkah kalian tentang luas lingkaran? Ya, benar sekali. Luas Lingkaran = πr2 .
Dengan demikian, kita dapat tentukan rumus volume tabung sebagai berikut.
Volume tabung = luas alas × tinggi
Volume tabung =
dengan:
r = panjang jari-jari tabung;
t = tinggi tabung; dan
atau π = 3,14.
Sekarang, mari kita kembali pada permasalahan Andi di atas.
Pada permasalahan tersebut, diketahui diameter drum 0,7 m dan tinggi drum 1 m. Andi ingin menghitung volume dalam satuan liter = dm³. Oleh karena itu, kita harus ubah dahulu diameter dan tinggi tabung tersebut dalam satuan dm.
Diameter = d = 0,7 m = 7 dm → dm
Tinggi = t = 1 m = 10 dm
Dengan demikian, kita dapatkan:

Jadi, volume air yang dibutuhkan adalah 385 dm3 (385 L).
Jika Andi ingin mengisi dengan dua ember yang masing-masing berisi 5,5 L, maka ia harus mengisi sebanyak 35 kali untuk memenuhi drum penyimpanan air tersebut.
Mudah bukan? Dengan mempelajari volume tabung, banyak hal yang bisa kita selesaikan dalam kehidupan sehari-hari. Untuk lebih memahami cara menentukan volume tabung, yuk perhatikan beberapa contoh soal di bawah ini.
Contoh
Contoh 1:
Sebuah tabung memiliki jari-jari 10 cm dan tinggi 20 cm. Tentukan:
a. Luas alasnya
b. Volume
Penyelesaian:
Dari soal, diketahui:
r = 10 cm
t = 20 cm
Dengan demikian, kita peroleh:
a. Luas alas tabung berupa lingkaran. Dengan demikian, untuk mencari luas alasnya, kita gunakan rumus luas lingkaran.
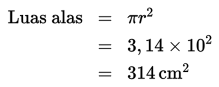
b. Volume tabung dapat ditentukan dengan cara berikut.

S1
Sebuah tabung memiliki jari-jari 10 dm dan tinggi 3 m. Volume tabung tersebut adalah ... L.
S2
Sebuah tabung memiliki volume 1232 cm³. Jika jari-jari tabung 14 cm, maka tinggi tabung tersebut adalah ... cm.
S3
Sebuah tabung memiliki volume 3140 cm³. Jika tinggi tabung 40 cm, maka panjang jari-jari tabung tersebut adalah ... cm.
S4
Sebuah tabung memiliki keliling alas 62,8 cm. Jika tingginya dua kali diameter alasnya, maka volume tabung tersebut adalah ... L.
S5
Sebuah tabung memiliki luas permukaan 1760 cm². Jika diketahui jari-jari tabung adalah 14 cm, maka volume tabung tersebut adalah ... cm³.
S6
Jika jari-jari suatu tabung diperbesar dua kali dari aslinya, sedangkan tingginya diperkecil setengah dari tinggi aslinya, maka volumenya adalah ....
S7
Sebuah tabung dengan selimut berbentuk persegi, memiliki jari-jari alas 7 m. Volume tabung tersebut adalah ... m³.
S8
Diketahui sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Jika jari-jari dan tinggi tabung tersebut masing-masing diperbesar dua kalinya, maka perbandingan volume tabung sebelum dan setelah diperbesar adalah ....
S9

Sebuah tabung padat yang memiliki keliling alas 125,8 cm dipotong menjadi dua tabung kecil yang berukuran sama. Jika tinggi tabung besar adalah 50 cm, volume tabung kecil adalah ... L.
S10

Gambar di atas menunjukkan sebuah tabung yang berada dalam tabung lain. Diketahui tinggi kedua tabung yaitu 10 cm dan jari-jari tabung yang besar adalah 20 cm. Jika diketahui volume tabung besar yang terletak di luar tabung kecil adalah 9420 cm³, maka jari-jari tabung kecil adalah ... cm.
