Contoh Soal Memahami Peluang Teoritik

Contoh Soal Memahami Peluang Teoritik - Agus dan Hendra sedang bermain ular tangga. Agus telah berada pada kotak nomor 95, sedangkan Hendra masih berada pada kotak nomor 76. Saat tiba giliran Agus untuk melambungkan dadunya, ia berharap mendapat mata dadu lima supaya dapat memenangkan permainan.

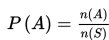
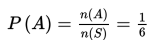
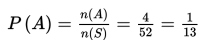
Menurut kalian, berapa peluang Agus untuk mendapatkan mata dadu lima?
Yuk temukan jawabannya padak topik ini!

Pengertian Titik Sampel dan Ruang Sampel

Sebelum berbicara lebih lanjut mengenai peluang teoretik suatu kejadian, ada baiknya kita mengetahui tentang pengertian titik sampel dan ruang sampel terlebih dahulu.

• Hasil yang mungkin terjadi dalam suatu percobaan disebut titik sampel.
• Himpunan titik-titik sampel pada suatu percobaan disebut ruang sampel.

Contoh 1 :

Pada peristiwa satu kali lemparan sebuah dadu, kejadian yang mungkin terjadi adalah {1}, {2}, {3}, {4}, {5}, dan {6}.

Titik sampel dari percobaan di atas adalah 1, 2, 3, 4, 5, dan 6. Sedangkan ruang sampelnya adalah S = { 1, 2, 3, 4, 5, 6 }.

Contoh 2 :

Pada peristiwa satu kali lemparan sebuah uang logam, kejadian yang mungkin terjadi adalah munculnya angka (A) atau gambar (G).

Titik sampel dari percobaan di atas adalah A dan G. Sedangkan ruang sampelnya adalah S = { A, G }.

Peluang Teoretik

Pada topik sebelumnya, kita telah membahas tentang peluang empirik yang merupakan peluang yang muncul dari hasil percobaan secara berulang kali.
Nah, dalam topik kali ini kita akan membahas tentang peluang teoretik suatu kejadian.

Peluang teoretik merupakan peluang yang menggunakan asumsi bahwa semua kejadian yang mungkin akan terjadi memiliki kemungkinan yang sama.

Peluang kejadian A dapat ditentukan dengan cara sebagai berikut :

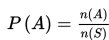
dengan S adalah ruang sampel, A adalah kejadian dalam suatu percobaan, n(A) adalah banyaknya kejadian A, dan n(S) adalah banyaknya anggota ruang sampel S.

Contoh 3 :

Mari kita kembali pada contoh pelemparan sebuah dadu sebanyak satu kali oleh Agus.

• Ruang sampel S = { 1, 2, 3, 4, 5, 6 } → n(S) = 6.
• jIka A adalah kejadian munculnya mata dadu 5, maka A = {5} → n(A) = 1.

Dengan demikian, peluang muncul mata dadu 5 adalah :

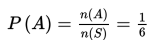
Contoh 4 :

Mario mengambil seperangkat kartu bridge. Ia berniat mengambil salah satu dari seperangkat kartu tersebut. Mario berharap mendapatkan kartu AS. Menurut kalian, berapakah peluang Mario untuk mendapatkan kartu AS tersebut?

Penyelesaian :

Banyaknya kartu dalam seperangkat kartu bridge adalah 52 buah → n(S) = 52.
Banyaknya kartu AS dalam seperangkat kartu bridge adalah 4 buah → n(A) = 4.

Jadi, peluang terambilnya kartu AS oleh Mario adalah :

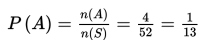
S1

Banyak anggota ruang sampel pada peristiwa pelemparan sebuah koin sebanyak satu kali adalah ….

S2

Pada peristiwa pelemparan sebuah dadu sebanyak satu kali, banyak kejadian muncul mata dadu genap adalah ….

S3

Sebuah koin dilempar sebanyak satu kali. Peluang muncul gambar adalah ….

S4

Dari seperangkat kartu bridge diambil sebuah kartu secara acak. Peluang terambil kartu bergambar sekop adalah ….

S5

Pada pelemparan sebuah dadu sebanyak satu kali, peluang muncul mata dadu lebih dari tiga adalah ….

S6

Dalam sebuah kotak terdapat 5 buah bola berwarna merah ,3 buah bola berwarna hijau, dan 2 buah bola berwarna biru. Jika diambil sebuah bola secara acak, peluang terambilnya bola berwarna biru adalah ….

S7

Banyak anggota ruang sampel pada satu kali pelemparan dua buah dadu secara bersamaan adalah .…

S8

Dua buah dadu dilempar bersamaan sebanyak satu kali. Peluang muncul mata dadu berjumlah 10 adalah ….

S9

Dua buah dadu dilempar bersamaan sebanyak satu kali. Peluang muncul pasangan mata dadu ganjil adalah ….

S10

Sebuah dadu dan sebuah koin dilempar bersamaan sebanyak satu kali. Banyak anggota ruang sampel adalah ….

Share this post