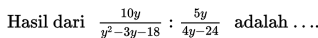Contoh Soal Faktorisasi Aljabar
Contoh Soal Faktorisasi Aljabar - Hukum distributif bentuk aljabar dapat dinyatakan sebagai berikut :
Faktorisasi Selisih Dua Kuadrat
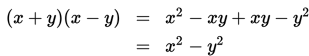
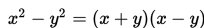
Faktorisasi ax^2 + bx + c dengan a = 1
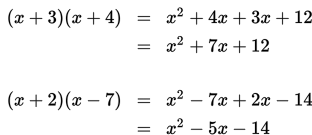
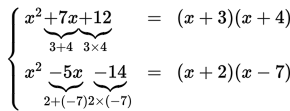
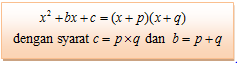
Faktorisasi ax^2 + bx + c dengan a ≠ 1

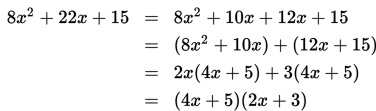
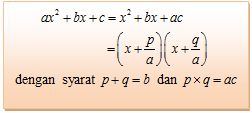
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Contoh 2 :
Contoh 3 :
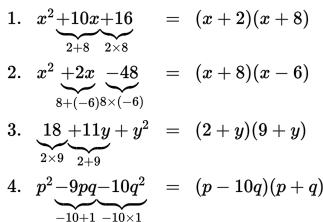
Contoh 4 :
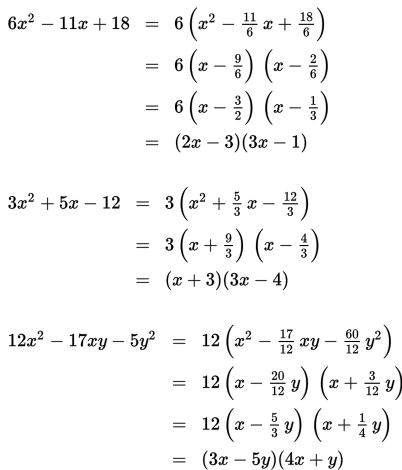
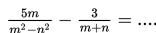

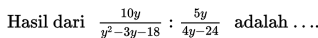
ab + ac = a(b + c)
dengan a, b, dan c sebarangan bilangan nyata.
dengan a, b, dan c sebarangan bilangan nyata.
Bentuk di atas menunjukkan bahwa bentuk penjumlahan suku-suku dapat dinyatakan sebagai bentuk perkalian faktor-faktor jika suku-suku dalam bentuk penjumlahan memiliki faktor yang sama (faktor persekutuan).
Dengan demikian, bentuk ab + ac dengan faktor persekutuan a dapat difaktorkan menjadi
a(b + c) yang terdiri dari dua faktor, yaitu a dan (b + c) .
a(b + c) yang terdiri dari dua faktor, yaitu a dan (b + c) .
Faktorisasi (pemfaktoran) adalah menyatakan bentuk penjumlahan suku-suku menjadi bentuk perkalian faktor-faktor. Selanjutnya, bentuk penjumlahan suku-suku pada bentuk aljabar yang memiliki faktor yang sama (faktor persekutuan) dapat difaktorkan dengan menggunakan hukum distributif.
Dalam faktorisasi, faktor yang diambil adalah faktor persekutuan terbesar, sehingga suku-suku yang berada di dalam tanda kurung tidak lagi memuat faktor persekutuan.
Faktorisasi Selisih Dua Kuadrat
Untuk setiap bilangan cacah x dan y, telah dijelaskan bahwa bentuk (x + y)(x - y) dapat dijabarkan sebagai berikut :
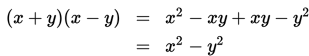
Bentuk tersebut dapat juga ditulis sebagai bentuk faktorisasi, yaitu :
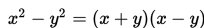
Bentuk x2 - y2 pada ruas kiri disebut selisih dua kuadrat, karena terdiri dari dua suku yang masing-masing merupakan bentuk kuadrat, dan merupakan bentuk pengurangan (selisih). Ruas kanan, yaitu (x + y)(x - y) merupakan bentuk perkalian faktor-faktor.
Berdasarkan hal tersebut, maka rumus faktorisasi selisih dua kuadrat adalah :
x2 - y2 = (x + y)(x - y)
x2 - y2 = (x + y)(x - y)
Faktorisasi ax^2 + bx + c dengan a = 1
Pada bahasan ini, akan kita pelajari tentang faktorisasi bentuk ax2 + bx + c dengan a = 1. Mari kita perhatikan bentuk aljabar berikut :
- x2 + 10x - 21 berarti a = 1, b = 10, dan c = -21
- x2 - 12x + 20 berarti a = 1, b = -12, dan c = 20
Pada bentuk ax2 + bx + c :
1. a disebut koefisien x2
2. b disebut koefisien x
3. c disebut bilangan konstan
1. a disebut koefisien x2
2. b disebut koefisien x
3. c disebut bilangan konstan
Untuk memahami faktorisasi bentuk ax2 + bx + c dengan a = 1, yang selanjutnya dapat kita tulis dengan x2 + bx + c , mari kita perhatikan uraian berikut.
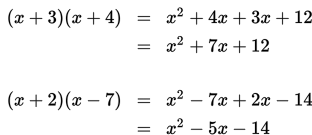
Dari penjabaran tersebut, diperoleh hubungan sebagai berikut :
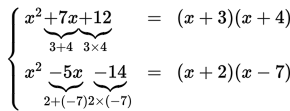
Ternyata faktorisasi bentuk x2 + bx + c dapat dilakukan dengan cara menentukan pasangan bilangan yang memenuhi syarat-syarat berikut :
- Bilangan konstan c merupakan hasil perkalian dari pasangan bilangan tersebut
- Koefisien x , yaitu b merupakan hasil penjumlahan dari pasangan bilangan tersebut.
Dengan demikian, dapat disimpulkan bahwa faktorisasi bentuk x2 + bx + c adalah :
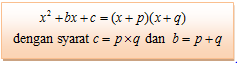
Faktorisasi ax^2 + bx + c dengan a ≠ 1
Pada topik sebelumnya, kalian telah belajar tentang perkalian suku dua. Apakah kalian masih ingat?

Dari bentuk pada ruas kanan, dapat disimpulkan bahwa untuk memfaktorkan 8x2 + 22x + 15 (lihat bentuk 2), terlebih dahulu suku 22x diuraikan menjadi dua suku (lihat bentuk 1) dengan aturan sebagai berikut :
- Jika koefisien kedua suku itu dijumlahkan, maka akan menghasilkan 22
- Jika koefisien kedua suku itu dikalikan, maka hasilnya sama dengan hasil kali koefisien dengan bilangan konstan, yaitu 120
Dengan demikian, pemfaktoran 8x2 + 22x + 15 dapat dilakukan dengan cara sebagai berikut :
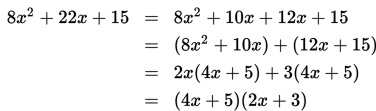
Dari uraian di atas, dapat ditarik kesimpulan berikut :
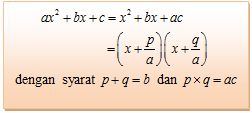
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Faktorkanlah bentuk-bentuk aljabar berikut.
1. 4a + 8
2. 9p3 + 15p2
3. 4x2y + 6xy2 - 8x2y2
Penyelesaian :
4a + 8
= 4(a) + 4(2)
= 4 (a + 2)
= 4(a) + 4(2)
= 4 (a + 2)
9p3 + 15p2
= 3p3(3) + 3p3(5p2)
= 3p3(3 + 5p2)
= 3p3(3) + 3p3(5p2)
= 3p3(3 + 5p2)
4x2y + 6xy2 - 8x2y2
= 2xy(2x) + 2xy(3y) - 2xy(4xy)
= 2xy(2x + 3y - 4xy)
= 2xy(2x) + 2xy(3y) - 2xy(4xy)
= 2xy(2x + 3y - 4xy)
Contoh 2 :
Faktorkanlah bentuk-bentuk aljabar berikut ini!
1. a2 - 49
2. 25x2 - 362
3. 9x4 - 4y2
4. 5m2 - 5n2
Penyelesaian :
a2 - 49
= a2 - 72
= (a + 7)(a - 7)
= a2 - 72
= (a + 7)(a - 7)
25x2 - 362
= (5x)2 - 62
= (5x + 6)(5x - 6)
= (5x)2 - 62
= (5x + 6)(5x - 6)
9x4 - 4y2
= (3x2)2 - (2y)2
= (3x2 + 2y)(3x2 - 2y)
= (3x2)2 - (2y)2
= (3x2 + 2y)(3x2 - 2y)
5m2 - 5n2
= 5(m2 - n2)
=5(m + n)(m - n)
= 5(m2 - n2)
=5(m + n)(m - n)
Contoh 3 :
Faktorkanlah bentuk-bentuk aljabar berikut!
1. x2 + 10x + 16
2. x2 + 2x - 48
3. 18 + 11y + y2
4. p2 - 9pq - 10q2
Penyelesaian :
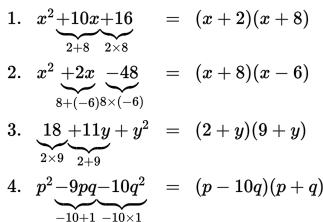
Contoh 4 :
Faktorkanlah bentuk-bentuk aljabar berikut ini!
1. 6x2 - 11x + 3
2. 3x2 + 5x - 12
3. 12x2 - 17xy - 5y2
Penyelesaian :
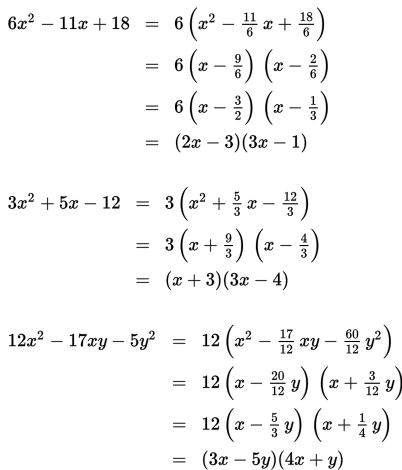
S1
Pada faktorisasi x6 - x2 = m(xn - 1), nilai m dan n berturut-turut adalah ....
S2
Faktorisasi dari 16p2 - 81q2 adalah ....
S3
Salah satu faktor linear dari hasil pemfaktoran (3a - 2)2 - (a - 1)2 adalah ....
S4
Faktorisasi 40 + 6x - x2 adalah ….
S5
Pemfaktoran dari 8x2 + 14xy - 15y2 adalah ….
S6
S7
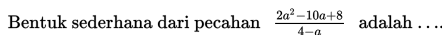
S8
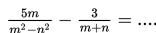
S9

S10