Contoh Soal Sifat-Sifat Fungsi Invers
Contoh Soal Sifat-Sifat Fungsi Invers - Kamu telah mengetahui bahwa suatu fungsi akan menghasilkan invers yang juga merupakan fungsi bijektif. Pada pembahasan kali ini, kita akan fokus pada sifat-sifat dari fungsi invers beserta kaitannya dengan komposisi fungsi.
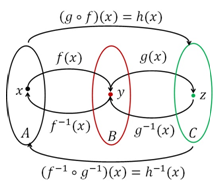
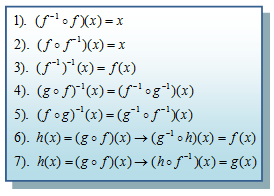
Misalkan fungsi f (x) dan g (x) merupakan fungsi-fungsi yang bijektif, maka invers dari kedua fungsi ini yaitu f -1 (x) dan g -1 (x) pastilah merupakan fungsi serta (f o g) (x), (g o f) (x),
(f -1 o g -1 ) (x), (g -1 o f -1 ) (x) dan komposisi lainnya juga mungkin merupakan fungsi. Pelajari diagram berikut ini dengan seksama.
(f -1 o g -1 ) (x), (g -1 o f -1 ) (x) dan komposisi lainnya juga mungkin merupakan fungsi. Pelajari diagram berikut ini dengan seksama.

Dari diagram di atas diketahui bahwa, fungsi f (x) memetakan setiap anggota dari himpunan A ke himpunan B dan g (x ) melanjutkan pemetaan ini dari setiap anggota di himpunan B ke himpunan C, sehingga fungsi komposisi (g o f) (x) memetakan setiap anggota di himpunan A langsung ke himpunan C.
Invers dari fungsi-fungsi tersebut melakukan pemetaan yang berkebalikan yaitu g -1(x) memetakan setiap anggota dari himpunan C ke himpunan B, dan f -1 (x) melanjutkan pemetaan dari himpunan B ke himpunan A, sehingga fungsi komposisi dari fungsi-fungsi invers ini yaitu (f -1 o g -1 ) (x) memetakan setiap anggota dari himpunan C langsung ke himpunan A. Dari penjelasan diatas dapat kita simpulkan sifat-sifat fungsi invers sebagai berikut.
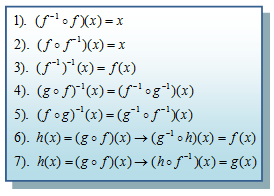
SOAL 1
Invers dari f (x) = , x ≠ 0 adalah ....
SOAL 2
Fungsi f (x) = -2x + 3 merupakan fungsi bijektif dari Ɍ → Ɍ. Jika h (x) merupakan komposisi fungsi f (x) dengan inversnya, maka h (x) = ....
SOAL 3
Jika diketahui invers dari f (x) adalah f -1 (x) = , maka f (x) adalah ….
SOAL 4
Apabila diketahui h (x) = (f o g) (x) dengan f (x) = 2x dan g (x)= , maka h -1 (x) = ....
SOAL 5
Diberikan dua fungsi f (x) = x 2 – 1 dan g (x) = 2x - 1 yang terdefinisi pada x ≥ 0. Jika h (x) = (g o f) (x), maka invers dari h (x) adalah ....
SOAL 6
Diketahui f -1 (x) = x + 2, x ϵ Ɍ dan g -1 (x) = merupakan invers dari fungsi bijektif f (x) dan g (x). Apabila h (x) = f (g (x)), maka h -1 (x) adalah ....
SOAL 7
Diketahui f (x) dan g (x) merupakan dua fungsi bijektif. Pernyataan yang salah diantara kelima peryataan berikut adalah ....
SOAL 8
Fungsi f, g, dan h memenuhi hubungan h (x) = f (g (x)). Apabila diketahui h (x) = x 3 + x dan g (x) = x untuk x Є Ɍ , maka f (x) = .....
SOAL 9
Diberikan fungsi h (x) = 3x - 12 dan f (x) = 2x - 7 yang terdefinisi untuk x ϵ Ɍ. Apabila h (x) = f (g (x)) maka g (x) = .…
SOAL 10
Diberikan dua fungsi f (x) = x 2 - 2x - 8, x ≥ 1 dan g (x) = , x ≥ 9. Apabila diketahui h (x) = g (f (x)), maka invers dari h (x) adalah .…
