Contoh Soal Permutasi

Contoh Soal Permutasi -

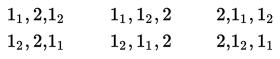
Permutasi

Kasus bendera pada awal topik ini merupakan salah satu contoh permutasi. Permutasi (P) adalah penyusunan suatu himpunan dari elemen-elemennya dengan memperhatikan urutan. Ada beberapa jenis permutasi yaitu permutasi n unsur, permutasi k dari n unsur, permutasi unsur yang sama, dan permutasi siklis. Mari simak penjelasannya berikut ini.

Permutasi n Unsur

Misalkan di sebuah kelas terdapat 20 siswa dan 20 tempat duduk. Menurut aturan perkalian, untuk tempat duduk pertama ada 20 siswa yang bisa menempatinya, tempat duduk kedua ada 19 siswa yang bisa menempatinya karena 1 siswa telah menempati tempat duduk yang pertama. Tempat duduk ketiga ada 18 siswa yang bisa menempatinya karena 2 siswa sudah menempati tempat duduk sebelumnya, hingga pada tempat duduk terakhir hanya 1 siswa yang tersisa untuk menempatinya. Ini berarti, banyak cara 20 siswa duduk dengan susunan berbeda adalah:

20 × 19 × 18 × 17 × 16 × ... × 3 × 2 × 1 atau dapat ditulis 20! (dibaca: 20 faktorial).

Ini berarti, banyak cara menyusun n objek/unsur yang berbeda adalah n!

Contoh:

Banyak cara menyusun buku Matematika, IPA, IPS, Bahasa Indonesia, dan Bahasa Inggris = 5! karena banyak buku = n = 5.

Permutasi k dari n Unsur

Perhatikan kembali kasus tempat duduk pada uraian permutasi n unsur. Jika pada baris depan terdapat 4 tempat duduk, maka menurut aturan perkalian banyak cara 4 dari 20 siswa akan menempati tempat duduk baris depan adalah 20 × 19 × 18 × 17 atau dapat ditulis:

20×19×18×17×16×...×3×2×116×15×...×3×2×1=20!16!=20!(20–4)!$\frac{20\times 19\times 18\times 17\times 16\times ...\times 3\times 2\times 1}{16\times 15\times ...\times 3\times 2\times 1}=\frac{20!}{16!}=\frac{20!}{(20–4)!}$

       Contoh di atas merupakan permutasi 4 dari 20 atau P(20,4) atau P204 atau 20P4 . Secara umum, ini dinyatakan sebagai permutasi k dari n unsur. Dengan demikian, banyak cara menyusun k unsur dari n unsur yang tersedia dengan memperhatikan urutan disebut permutasi k dari n unsur yaitu:

nPk=n!(n–k)!${}_n{P}_k=\frac{n!}{(n–k)!}$ dengan k ≤ n

Permutasi Unsur yang Sama

Bagaimana jika terdapat unsur yang sama? Mari perhatikan ilustrasi berikut.

       Dari angka 1, 2, 1 akan disusun dengan urutan yang berbeda. Oleh karena ada dua angka 1, maka akan kita bedakan dengan memberi indeks yaitu 11 dan 12. Susunan yang dapat terbentuk adalah:

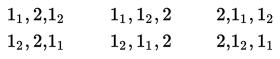
       Jika angka 1 diberi indeks maka banyak susunan yang terbentuk adalah 3! = 3 × 2 × 1 = 6 susunan, tetapi angka 11 dan 12 sebenarnya sama sehingga susunan yang terbentuk hanya 3 susunan yaitu 1, 2, 1; 1, 1, 2; dan 2, 1, 1. Susunan ini dapat dinyatakan sebagai 3×2×12×1=3!2!=3$\frac{3\times 2\times 1}{2\times 1}=\frac{3!}{2!}=3$. Pada perhitungan tersebut, dua buah angka 1 diwakili oleh 2! dan total tiga buah angka diwakili 3!. Dengan demikian, jika dari sebanyak n unsur yang tersedia terdapat m1, m2, m3, ... unsur yang sama, maka banyak permutasi dapat ditentukan dengan:

P=n!m1!×m2!×m3!×...$P=\frac{n!}{m_1!\times m_2!\times m_3!\times ...}$ dengan m1+m2+m3+...≤n$m_1+m_2+m_3+...\le n$

Permutasi Siklis (Melingkar)

Bagaimana jika susunan permutasi disajikan dalam bentuk melingkar? Mari perhatikan ilustrasi berikut.

       Misalkan ada 4 orang (A, B, C, dan D) yang akan duduk di sekeliling meja bundar, sehingga ada 6 susunan duduk yang mungkin seperti pada gambar di atas. Oleh karena lingkaran tidak mempunyai titik ujung maka haruslah ditetapkan 1 orang (unsur/objek) sebagai acuan. Pada gambar, A dijadikan sebagai acuan, sehingga posisi A tetap. Ini berarti, kita cukup menentukan banyak susunan duduk dari 3 orang lainnya dengan aturan perkalian. Jadi, banyak susunan duduk dari 4 orang (A, B, C, dan D) yang akan duduk melingkar yaitu (4 – 1)! = 3! = 3 × 2 × 1 = 6 susunan.

       Permutasi seperti ini disebut permutasi siklis yaitu banyak cara n unsur dapat disusun secara melingkar adalah P = (n - 1)!

SOAL 1

Nilai dari 12P3 = ....

SOAL 2

Banyak cara 6 orang siswa berdiri berjajar membentuk lingkaran adalah ....

SOAL 3

Dari 8 siswa yang mengikuti babak final olimpiade matematika, akan ditentukan masing-masing 1 siswa yang meraih juara 1, 2, dan 3. Banyak cara menentukan urutan siswa yang akan meraih juara adalah ...

SOAL 4

Jika terdapat 3 bola merah dan 2 bola putih, maka banyak susunan berbeda yang dapat dibentuk oleh bola-bola tersebut adalah ....

SOAL 5

Nilai n yang memenuhi n - 1P2 = 90 adalah ....

SOAL 6

Ada 2 kelompok kelereng yang akan disusun memanjang. Kelompok pertama terdiri dari 3 kelereng putih dan 2 kelereng biru. Kelompok kedua terdiri dari 2 kelereng kuning dan 4 kelereng hitam. Jika semua kelereng harus diletakkan berdampingan dengan kelompoknya, maka banyak cara menyusun kelereng tersebut adalah ....

SOAL 7

Pak Amin ingin memberi kode pada tipe lemari yang merupakan barang dagangannya dengan kode 6 digit. Dua digit pertama dapat diisi dengan huruf-huruf pembentuk kata “AMIN”, lalu 4 digit berikutnya akan disusun dari 5 angka ganjil tanpa berulang. Banyak susunan kode yang dapat dibentuk adalah ....

SOAL 8

Dari 8 buku terdapat 3 di antaranya memiliki judul yang sama. Banyak cara menyusun buku-buku tersebut jika 3 buku dengan judul yang sama tidak boleh berdampingan adalah ....

SOAL 9

Sebuah keluarga terdiri dari ayah, ibu, kakek, nenek, dan 3 orang anak. Mereka akan menempati meja makan bundar. Jika ayah dan ibu harus duduk berdampingan, demikian juga dengan kakek dan nenek, maka banyak cara yang dapat disusun untuk duduk mengelilingi meja adalah ....

SOAL 10

Banyak cara menyusun huruf-huruf pembentuk kata “MATEMATIKA” jika semua huruf vokal harus diletakan di urutan depan adalah ....

Share this post