Contoh Soal Pengertian dan Notasi Vektor

Contoh Soal Pengertian dan Notasi Vektor - Berdasarkan arah, besaran terdiri atas dua kelompok yaitu besaran skalar dan besaran vektor. Untuk memahami perbedaan kedua besaran tersebut, mari perhatikan beberapa hasil pengukuran pada tabel berikut.

       Dapatkah kamu membedakan kedua hasil pengukuran tersebut? Perbedaannya terletak pada arah yang menyertai pengukuran. Pengukuran A tidak disertai dengan arahnya. Pengukuran yang demikian mengukur besaran skalar. Pada pengukuran B, ada penjelasan tentang arahnya, sehingga pengukuran tersebut mengukur besaran vektor. Besaran-besaran seperti panjang, massa, waktu, dan besaran lain yang tidak memerlukan penjelasan tentang arah digolongkan sebagai besaran skalar, sedangkan besaran-besaran seperti perpindahan, kecepatan, gaya dan besaran lain yang memerlukan penjelasan tentang arah digolongkan sebagai besaran vektor.

Pengertian Vektor

Vektor didefinisikan sebagai jenis besaran yang memiliki besar (nilai) dan arah. Secara grafis vektor dapat dilambangkan sebagai ruas garis berarah. Untuk memahami cara melambangkan suatu vektor, perhatikan contoh berikut.

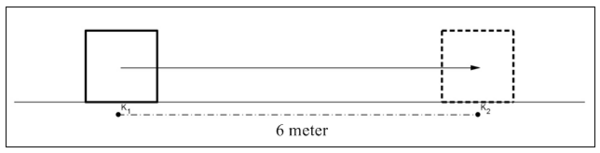
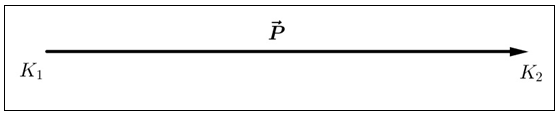
Pada gambar di atas, kubus K digeser kearah kanan sejauh 6 meter dari posisi K1 ke posisi K2. Vektor perpindahan kubus ini dapat dilambangkan sebagai ruas garis berarah.

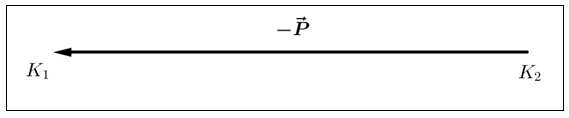
Besar vektor perpindahan ini dapat dilambangkan sebagai P→$\overrightarrow{P}$ = 6 meter. Namun, apabila kubus K digeser dengan arah berlawanan namun dengan jarak yang sama, maka vektor perpindahan kubus tersebut dinyatakan sebagai vektor negatif atau −P→$-\overrightarrow{P}$.

Oleh karena itu, notasi untuk nilai vektor dinyatakan dalam tanda mutlak, sehingga panjang vektor −P→$-\overrightarrow{P}$ adalah |−P→|$|-\overrightarrow{P}|$ = 6 meter.

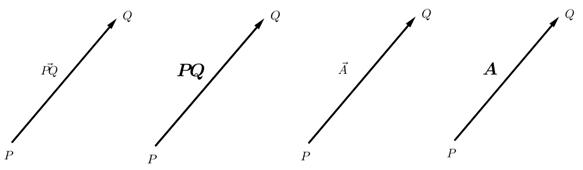
       Dalam menggambar ruas garis berarah untuk menyatakan vektor, perlu diperhatikan perbandingan dari panjang vektor yang digambar. Dengan kata lain, apabila terdapat vektor dengan panjang 5 m, 6 m, dan 10 m, maka kamu dapat menggambar ruas garis berarah dengan panjang 5 cm, 6 cm, dan 10 cm pada satu bidang gambar untuk mencegah kebingungan saat menganalisis vektor-vektor tersebut. Terdapat beberapa kesepakatan dalam menyatakan vektor sebagai ruas garis berarah seperti yang digambarkan pada contoh berikut.

Oleh karena cukup sulit untuk menebalkan tulisan huruf dengan pena, maka sebaiknya gunakan tanda panah di atas lambang vektor sebagai alternatif penulisannya.

Notasi Vektor

Kadangkala, terdapat banyak vektor yang terlibat dalam suatu perhitungan. Akibatnya, penggunaan ruas garis berarah menjadi tidak efektif karena keterbatasan bidang gambar. Oleh karena itu, dibutuhkan suatu notasi matematika yang dapat menyatakan vektor secara lengkap. Agar kamu lebih paham, perhatikan analisis berikut.

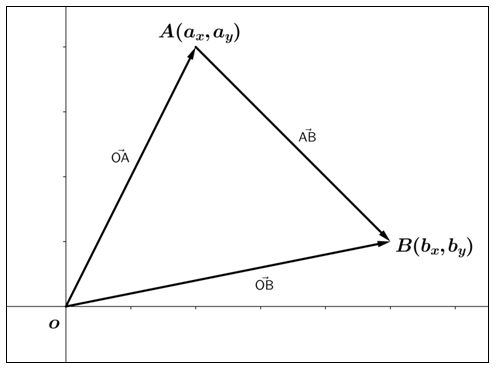
       Vektor yang berpangkal dititik O (0, 0) dan berujung di A (ax, ay) dapat dinyatakan sebagai vektor OA−→−=⟨ax–0,ay−0⟩=⟨ax,ay⟩$\overrightarrow{OA}=⟨a_x–0,a_y-0⟩=⟨a_x,a_y⟩$. Dengan cara yang sama, kita dapat menyatakan vektor OB−→−=⟨bx–0,by−0⟩=⟨bx,by⟩$\overrightarrow{OB}=⟨b_x–0,b_y-0⟩=⟨b_x,b_y⟩$. Ini berarti, vektor AB−→−$\overrightarrow{AB}$ dapat dinotasikan dengan cara serupa, sehingga diperoleh notasi vektor AB−→−=⟨bx–ax,by–ay⟩$\overrightarrow{AB}=⟨b_x–a_x,b_y–a_y⟩$. Pemilihan penggunaan kurung sudut daripada kurung biasa adalah untuk menghindari kebingungan antara notasi titik dan notasi vektor.

       Panjang suatu vektor dapat ditentukan dengan menggunakan rumus Pythagoras. Panjang dari ketiga vektor tersebut berturut-turut adalah:

∣∣∣OA−→−∣∣∣=a2x+a2y−−−−−−√$\left|\overrightarrow{OA}\right|=\sqrt{a_x^2+a_y^2}$

∣∣∣OB−→−∣∣∣=b2x+b2y−−−−−−√$\left|\overrightarrow{OB}\right|=\sqrt{b_x^2+b_y^2}$

∣∣∣AB−→−∣∣∣=(bx−ax)2+(by−ay)2−−−−−−−−−−−−−−−−−−√$\left|\overrightarrow{AB}\right|=\sqrt{{(b_x-a_x)}^2+{(b_y-a_y)}^2}$

Selain menggunakan kurung sudut, kamu juga dapat menggunakan notasi berikut untuk menyatakan vektor V→=⟨vx,vy⟩$\overrightarrow{V}=⟨v_x,v_y⟩$.

V→=(vx,vy)$\overrightarrow{V}=(v_x,v_y)$

V→=(vxvy)$\overrightarrow{V}=\left(\begin{array}{c}{v}_x\\ v_y\end{array}\right)$

V→=vxi+vyj$\overrightarrow{V}=v_{x}i+v_{y}j$

       Kamu harus konsisten dalam menggunakan notasi untuk menghindari kerancuan. Adapun notasi-notasi vektor khusus adalah sebagai berikut.

• Notasi untuk suatu vektor yang tidak memiliki panjang (0 satuan) adalah 0→$\overrightarrow{0}$.
• Notasi untuk vektor-vektor dengan panjang satu satuan (vektor satuan) adalah i→=⟨1,0⟩danj→=⟨0,1⟩$\overrightarrow{i}=⟨1,0⟩\mathrm{d}\mathrm{a}\mathrm{n}\overrightarrow{j}=⟨0,1⟩$.

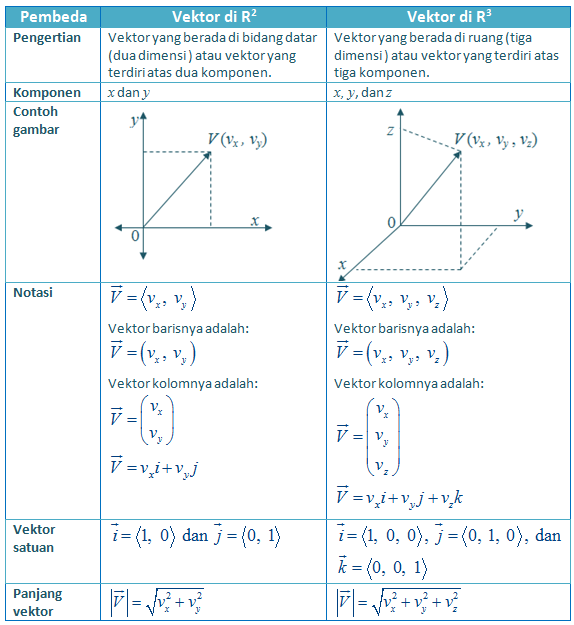
       Uraian di atas membahas tentang notasi vektor di R2 . Selain berada di R2 , vektor juga berada di R3 , bahkan Rn . Namun, yang paling umum dipelajari adalah vektor di R2dan R3 . Mari pahami perbedaannya melalui tabel di bawah ini.

Perbedaan antara Vektor di R2 dan R3

SOAL 1

Vektor adalah ….

SOAL 2

Hasil pengukuran berikut ini yang bukan merupakan besaran vektor adalah ….

SOAL 3

Sandy berlari mengelilingi lapangan tepat satu putaran penuh. Jika keliling lapangan 500 meter, maka besar vektor perpindahan Sandy adalah ....

SOAL 4

Diketahui:
A→=⟨1,1⟩,B→=⟨3,4⟩,C→=⟨4,3⟩,D→=⟨6,8⟩,danE→=⟨8,5⟩$\overrightarrow{A}=⟨1,1⟩,\overrightarrow{B}=⟨3,4⟩,\overrightarrow{C}=⟨4,3⟩,\overrightarrow{D}=⟨6,8⟩,\mathrm{d}\mathrm{a}\mathrm{n}\overrightarrow{E}=⟨8,5⟩$.

Vektor terpanjang adalah ….

SOAL 5

Sebuah partikel berpindah dari titik P (2, 6) ke titik Q (1, 7). Vektor yang tepat untuk menyatakan perpindahan partikel tersebut adalah ….

SOAL 6

Diketahui P→=⟨1,2⟩,Q→=⟨2,1⟩,R→=⟨2,4⟩,S→=⟨4,4⟩,T→=⟨3,9⟩,$\overrightarrow{P}=⟨1,2⟩,\overrightarrow{Q}=⟨2,1⟩,\overrightarrow{R}=⟨2,4⟩,\overrightarrow{S}=⟨4,4⟩,\overrightarrow{T}=⟨3,9⟩,$danU→=⟨9,3⟩$\mathrm{d}\mathrm{a}\mathrm{n}\overrightarrow{U}=⟨9,3⟩$. Vektor yang memiliki arah yang sama adalah ….

SOAL 7

Vektor dua dimensi M−→danN→$\overrightarrow{M}dan\overrightarrow{N}$ memiliki panjang berturut-turut 3 dan 4 satuan. Jika M+N−→−−−−=5$\overrightarrow{M+N}=5$ satuan, maka nilai dari ∣∣∣M−N−→−−−−∣∣∣$\left|\overrightarrow{M-N}\right|$adalah … satuan.

SOAL 8

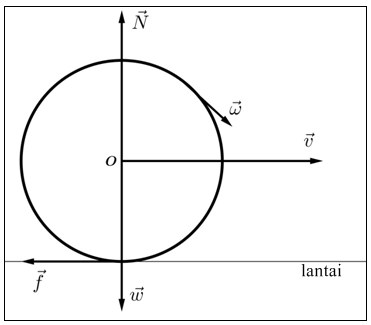
Gambar berikut menunjukkan beberapa gaya yang terlibat saat sebuah bola bowling menggelinding di lantai yang licin.

Diketahui v→$\overrightarrow{v}$ menyatakan vektor kecepatan, w→$\overrightarrow{w}$menyatakan vektor berat bola, N→$\overrightarrow{N}$ menyatakan vektor normal terhadap berat bola, f→$\overrightarrow{f}$menyatakan vektor gesekan bola dengan lantai, dan ω→$\overrightarrow{\omega }$ menyatakan kecepatan sudut bola. Agar saat menggelinding bola tetap berada di lantai, vektor yang memiliki besar yang sama adalah ....

SOAL 9

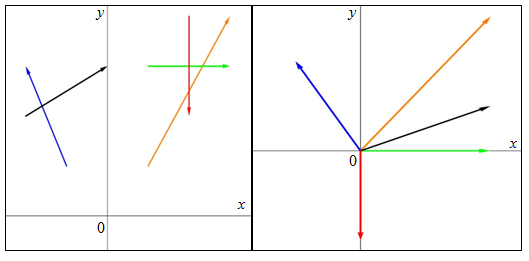
Dua orang siswa yaitu Rani dan Ronald, sedang menghitung 5 vektor perpindahan dengan cara yang berbeda. Rani menghitungnya langsung dari vektor-vektor yang tergambar. Ronald menghitungnya dengan cara menggeser setiap vektor tanpa memutarnya, sehingga setiap pangkal vektor berimpit di titik asal. Vektor-vektor tersebut disajikan pada gambar berikut.

Berdasarkan langkah perhitungan yang mereka lakukan, pernyataan berikut ini yang benar adalah ….

SOAL 10

Vektor-vektor dalam dimensi 3 (R3 ) dapat dinyatakan dalam komponen-komponen pembentuknya seperti v→=⟨v1,v2,v3⟩$\overrightarrow{v}=⟨v_1,v_2,v_3⟩$. Jika suatu partikel bergerak dalam ruang dari titik P = (p1 , p2 , p3) ke titik Q = (q1 , q2 , q3), maka vektor yang sesuai untuk menyatakan perpindahan ini adalah ….

Share this post