Contoh Soal Operasi Pembagian pada Suku Banyak oleh Bentuk Kuadrat
Contoh Soal Operasi Pembagian pada Suku Banyak oleh Bentuk Kuadrat - Pada topik sebelumnya, kalian telah mempelajari operasi pembagian pada suku banyak oleh bentuk linear. Apakah kalian masih ingat? Tentu iya. Lantas bagaimana dengan operasi pembagian pada suku banyak oleh bentuk kuadrat? Kalian belum paham bukan?
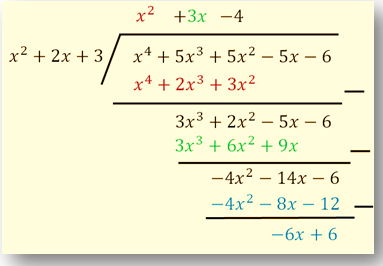
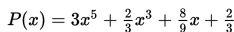
oleh q (x ) = 3x 2 - 4x + 1 adalah....
Untuk memahaminya, ayo pelajari topik ini dengan seksama.
Kalian tentu tidak asing lagi dengan bentuk kuadrat (ax 2 + bx + c ) dimana a, b, c ∈ R dan a ≠ 0. Kalian juga pasti masih ingat bagaimana cara memfaktorkan bentuk kuadrat tersebut kedalam faktor-faktor linearnya. Nah, pengetahuan tersebut akan mempermudah kalian dalam mempelajari topik kali ini.
Pada topik ini kita akan mempelajari pembagian pada suku banyak oleh bentuk kuadrat (ax 2 + bx + c ). Pembagian oleh bentuk ini dapat kalian lakukan dengan cara yang sama dengan pembagian sebelumnya, yaitu menggunakan metode pembagian bersusun dan metode skema (Horner). Apakah cara yang digunakan sama persis dengan pembagian oleh bentuk linear? Ataukah ada sesuatu yang membedakan? Untuk tahu jawabannya, mari kita simak penjelasan berikut ini.
Metode Pembagian Bersusun
Variasi pembagi dari suatu suku banyak tidak berpengaruh besar terhadap penerapan metode pembagian bersusun. Apabila suatu suku banyak P (x ) dibagi dengan bentuk kuadrat q (x ) = ax 2 + bx + c , perhitungan hasil bagi dan sisanya tidak jauh berbeda dengan pembagian oleh bentuk linear (x - k ) atau (ax + b ). Untuk memperjelas bagaimana pembagian ini dilakukan, mari kita perhatikan contoh berikut.
Contoh:
Tentukan sisa dan hasil pembagian apabila suku banyak P (x ) = x 4 + 5x 3 + 5x 2 - 5x - 6 dibagi dengan bentuk kuadrat q (x ) = x 2 + 2x + 3.
Penyelesaian:
Mari kita terapkan metode pembagian bersusun yang telah kita pelajari sebelumnya sehingga didapat
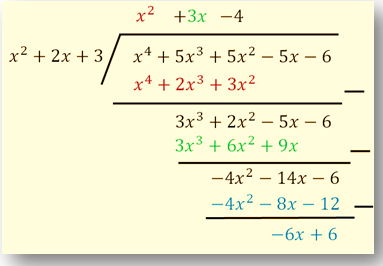
Jadi kita peroleh hasil dan sisa dari pembagian ini berturut-turut adalah H (x ) = x 2 + 3x -4 dan s (x ) = -6x + 6.
Metode pembagian bersusun selalu dapat digunakan untuk membagi suatu suku banyak berderajat n dengan suku banyak lain yang berderajat kurang dari atau sama dengan n. Dalam metode ini dibutuhkan ketelitian dan konsentrasi yang baik saat menyusun pembagian, karena satu saja kesalahan kecil dapat mengacaukan perhitungan kalian.
SOAL 1
Agar suatu pembagian suku banyak yang melibatkan pembagi q (x ) = 2x 2 + x - 3 dapat dikerjakan dengan metode Horner, maka bentuk ini harus difaktorkan. Faktor-faktor dari q (x ) adalah....
SOAL 2
Sisa pembagian dari P (x ) = x 4 + x 3 + x 2 + x + 1
oleh q (x ) = x 2 + x + 1 adalah....
SOAL 3
Hasil pembagian dari P (x ) = 2x 4 - x 3 + 2x 2 - x + 1
oleh q (x ) = x 2 - x + 2 adalah....
SOAL 4
Sisa pembagian dari P (x ) = 4x 4 + 3x 3 + 2x 2 + x
oleh q (x ) = x 2 - x adalah....
SOAL 5
Hasil bagi dari P (x ) = x 4 + 2x 3 + x 2 + 2x + 1
oleh q (x ) = x 2 - 1 adalah....
SOAL 6
Salah satu syarat pembagian suku banyak P (x ) oleh bentuk kuadrat q (x ) = ax 2 + bx + c dapat dilakukan dengan metode Horner adalah....
SOAL 7
Hasil pembagian dari
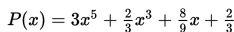
oleh q (x ) = 3x 2 - 4x + 1 adalah....
SOAL 8
Suku banyak P (x ) = x 4 + 2x 3 + 4x 2 + Ax + B
oleh q (x ) = x 2 + 2x + 3 memberikan sisa s (x ) = x + 1.
Nilai dari A + B adalah....
SOAL 9
Hasil bagi dan sisa pembagian dari
P (x ) = x 5 + x 4 + x 3 + x 2 + x + 1
oleh q (x ) = 2x 2 - 3x +1 adalah....
SOAL 10
Hasil bagi dan sisa pembagian dari
P (x ) = x 8 - 16
oleh q (x ) = x 2 - 2 adalah....
